Ukázka možností interpolace dat v softwaru Matlab
Transkript
Ukázka možností interpolace dat v softwaru Matlab Ing. Stanislav Olivík 1 Anotace: V následujícím textu bude čtenář seznámen s několika základními funkcemi softwaru Matlab, pomocí nichž může interpolovat data mezi zadanými (naměřenými) hodnotami. Na výběr je interpolace funkcí po částech konstantní, lineární interpolace, interpolace kubickou křivkou a také spline křivkou. 1. Úvod Software Matlab (zde ve verzi 7.0.1) nabízí v základním balíčku funkcí také několik funkcí umožňující interpolaci (a také extrapolaci) dat. Pro interpolaci funkčních hodnot y v závislosti na x ( y = f (x) ) je k dispozici funkce interp1. Pro interpolaci funkčních hodnot z v závislosti na x, y ( z = f ( x, y ) ) je k dispozici funkce interp2. Volumetrická data ( v = f ( x, y, z ) ) mohou být interpolována funkcí interp3. Pro vícedimenzionální data je zde funkce interpn. V tomto příspěvku budou přiblíženy pouze možnosti interpolace v rovině (2D) a prostoru (3D). 2. Interpolace v rovině Pro interpolaci hodnot y = f (x) se používá funkce interp1. Základní syntaxe je YI = INTERP1(X,Y,XI), kde X je vektor bodů na ose x, vektor Y obsahuje hodnoty v bodech vektoru X, XI je nové dělení intervalu vymezeném vektorem X (jiné než X) a YI je vektor interpolovaných hodnot. Hodnoty z vektorů X a Y se použijí jako opěrné body, jimiž se proloží požadovaná křivka. Hodnoty vektoru YI se následně počítají jako funkční hodnoty křivky v bodech vektoru XI. Dělení intervalu XI může být jakkoliv jemné či hrubé a nemusí obsahovat původní body z vektoru X. Přednastaveným typem interpolace je interpolace lineární. Dalšími možnými typy interpolace jsou: o 'nearest' - nejbližší soused (po částech konstantní funkce) o 'linear' - lineární interpolace o 'spline' - po částech kubická spline interpolace (SPLINE) o 'pchip' - po částech kubická interpolace zachovávající tvar (shape-preserving) o 'cubic' - stejná metoda jako 'pchip' o 'v5cubic' - kubická interpolace z verze 5, která neumožňuje extrapolaci a používá 'spline' pro neuniformní dělení X. Tyto metody se zadávají pomocí syntaxe YI = INTERP1(X,Y,XI,'method'). 1 Katedra matematiky, Fakulta stavební, České vysoké učení technické v Praze email: [email protected] Obr. 1: Rozdíly mezi jednotlivými typy interpolací. Funkce y=cosx. Extrapolace dat se zadává pomocí stejné funkce jako interpolace, pouze se přidá parametr ‘extrap’: YI = INTERP1(X,Y,XI,'method','extrap'). Extrapolace je možná pouze pro metody ‘cubic’, ‘pchip’ a ‘spline’. Obr. 2: Ukázka extrapolace spline křivkou a pchip polynomem. Obr. 3: Ukázka extrapolace stejné funkce stejnými metodami jako u Obr. 2 . Menší počet opěrných bodů. Jak je patrno z Obr. 2 a Obr. 3, extrapolované části křivky pokračují podle předpisu poslední interpolované části křivky (mezi posledními dvěma opěrnými body). Pro interpolaci pomocí spline křivky volá funkce interp1 funkci s názvem spline. Základní nastavení této funkce je takové, že vytváří přirozený spline (první i druhé derivace v koncových bodech křivky jsou rovny nule). Je zde však i možnost zadat velikosti krajních derivací, tedy tečný vektor křivky v krajních bodech. V tom případě se zadá vektor Y o dvě hodnoty delší než vektor X. První a poslední hodnota je v tomto případě brána jako velikost první derivace v krajních bodech (Obr. 4). Funkce spline umožňuje interpolovat a extrapolovat při uniformním i neuniformním dělení X. Obr. 4: Rozdíl mezi spline křivkou bez zadaných krajních derivací a se zadanými krajními derivacemi. Funkce spline také rozlišuje počet zadaných bodů. Pokud nejsou zadány krajní derivace a jsou zadány dva body, použije se lineární interpolace. Jsou-li zadány tři body bez krajních derivací, pak se těmito body proloží parabola. V ostatních případech se jednotlivé oblouky spline křivky počítají jako Hermitův interpolační polynom třetího stupně [1]. Pro výpočet koeficientů interpolačního polynomu je zapotřebí znát souřadnice opěrných bodů a též tečné vektory ke křivce v těchto bodech. Jelikož nejsou hodnoty prvních derivací známy (kromě krajních bodů), je nutno je dopočítat. Vypočítají se ze soustavy lineárních rovnic s třídiagonální maticí. Pro čtyři zadané body, nezadané krajní derivace, uniformní parametrizaci a krok X rovný jedné, má tato matice podobu 1 1 0 0 2 4 1 0 . (1) 0 1 4 2 0 0 1 1 Pravá strana se počítá podle vztahů b1 = [((x b2 = 3 ( x3 − x 2 )( y 2 − y1 ) + ( x 2 − x1 )( y 3 − y 2 ) b3 = 3 ( x 4 − x3 )( y 3 − y 2 ) + ( x3 − x 2 )( y 4 − y 3 ) [ ] − x1 ) + 2 ( x3 − x1 ))(x3 − x 2 )( y 2 − y1 ) + ( x 2 − x1 ) ( y 3 − y 2 ) ( x3 − x1 ) 2 2 . ] b4 = ( x 4 − x3 ) ( y 3 − y 2 ) + (2( x 4 − x 2 ) + ( x 4 − x3 ))( x3 − x 2 )( y 4 − y 3 ) ( x 4 − x 2 ) 2 (2) Vypočítané hodnoty prvních derivací spolu s vektory X, Y a diferencemi mezi sousedními hodnotami X a Y vstupují do výpočtu koeficientů kubického polynomu. Pokud jsou zadány derivace v krajních bodech, liší se jak matice, tak vektor pravých stran. Při zachování ostatních podmínek jako v předchozím případě pak má matice podobu 1 1 0 0 1 4 1 0 (3) 0 1 4 1 0 0 1 1 a vektor pravých stran se počítá ze vztahů b1 = y1′ ( x3 − x 2 ) b2 = 3 ( x3 − x 2 )( y 2 − y1 ) + ( x 2 − x1 )( y 3 − y 2 ) b3 = 3 ( x 4 − x3 )( y 3 − y 2 ) + ( x3 − x 2 )( y 4 − y 3 ) b4 = y 4′ ( x3 − x 2 ) . (4) Při interpolaci metodami ‘pchip’ a ‘cubic’ se použije též Hermitův interpolační polynom třetího stupně. Na rozdíl od spline však není zajištěna spojitost druhých derivací a výsledná křivka respektuje monotónnost dat a méně osciluje kolem zadaných bodů. Viz Obr. 5. Obr. 5: Příklad rozdílu mezi spline a pchip interpolací. Upravený příklad z [1] Hermitův interpolační polynom třetího stupně (‘pchip’ – Piecewise Cubic Hermite Interpolating Polynomial) lépe interpoluje po částech monotónní data. To je dáno tím, že při výpočtu prvních derivací dává větší váhu bodům, v jejichž obou sousedních bodech se funkční hodnota buď mění výrazně, nebo naopak velmi málo, tj. v jejichž okolí jsou funkční hodnoty monotónní. Následující dva obrázky (Obr. 6 a Obr. 7) jasně ukazují, jak moc záleží na počtu a rozmístění opěrných bodů. Oba znázorňují interpolaci spline křivkou a kubickým π 5π > a krok polynomem mezi body funkce y = cos x . Na Obr. 6 je použit interval < , 3 3 π π 7π π generování původní sítě opěrných bodů . Obr. 7 je pro interval < , > a krok . 3 4 4 2 Obr. 6: Část funkce y = cosx. Interpolace spline křivkou a kubickým polynomem. Obr. 7: Část funkce y = cosx. Interpolace spline křivkou a kubickým polynomem. 3. Interpolace v prostoru V prostoru přichází do hry interpolace ve dvou směrech. Nabízené metody zde jsou: o 'nearest' - nejbližší soused (po částech konstantní plocha) o 'linear' - bilineární interpolace o 'spline' - spline interpolace o 'cubic' - bikubická interpolace Nejjednodušší a nejméně přesnou je zde opět interpolace metodou nejbližšího souseda, tedy po částech konstantní plochou. Další metodou je bilineární interpolace. Ani tato metoda nedosahuje u složitějších ploch dobré výsledky, jak dokládá Obr. 8, který ukazuje lineární interpolaci mezi uzlovými body hrubé sítě, ve srovnání s Obr. 11, na němž je zobrazena původní funkce, z níž byla vygenerována tato hrubá síť bodů. Spline interpolace vytvoří plochu tenzorového součinu. Vyžaduje uniformní dělení X a aby data vektoru X byla monotónně rostoucí. V okrajových bodech původní sítě se určí první derivace, a to proložením přirozené spline křivky. Postupným interpolováním parametrických křivek kubickými spline křivkami se dopočítají obě parciální derivace ve všech uzlových bodech sítě. Na okrajových křivkách se určí druhé smíšené parciální derivace kubickou spline interpolací vektorů prvních derivací. Další interpolací se dopočítají hodnoty druhé smíšené derivace ve všech bodech sítě. Výpočet mezilehlých bodů plochy při bikubické interpolaci je odvozen z kubické konvoluce, která se používá pro interpolaci digitálního obrazu při změně jeho velikosti. Algoritmus kubické konvoluce počítá hodnotu nového bodu jako vážený průměr z 16 nejbližších okolních bodů. Největší váha se přiřazuje nejbližším bodům a nejmenší naopak bodům nejvzdálenějším. Obr. 8: Bilineární interpolace. Upravený příklad z [1] Obr. 9: Bikubická interpolace. Upravený příklad z [1] Obr. 10: Spline interpolace. Upravený příklad z [1] Obr. 11: Původní funkce na jemnější síti. Upravený příklad z [1] 4. Závěr Jako vždy, i při interpolaci dat záleží na datech vstupních. Pokud jsou vstupní data rozmístěna v hrubé síti, je volba typu interpolace zásadním rozhodnutím, které výrazně ovlivní výsledné hodnoty. Naopak, při dalším zjemňování jemné sítě se budou hodnoty interpolované různými způsoby lišit jen málo. Tedy kromě interpolace funkcí po částech konstantní. Literatura [1] Matlab help [2] Ježek, F.: Geometrické a počítačové modelování, Pomocný učební text, ZČU Plzeň, 2000 [3] Weisstein, E.W.: Hermite Polynomial. From MathWorld [online], URL: http://mathworld.wolfram.com/HermitePolynomial.html [4] Mathews, J.H.: Lab for Hermite Polynomial Interpolation [online], URL: http://math.fullerton.edu/mathews/ Tento příspěvek vznikl v rámci výzkumu pro grant FRVŠ G1 392
Podobné dokumenty
AKCELERACE EVOLUCE PRAVIDEL CELULÁRNÍCH
 CA můžeme rozdělit na synchronní a asynchronní. To závisí na způsobu aktualizace stavů buněk.
V synchronním CA dochází periodicky u každé buňky ke kontrole stavu okolních buněk. Těmto
buňkám se řík...
CA můžeme rozdělit na synchronní a asynchronní. To závisí na způsobu aktualizace stavů buněk.
V synchronním CA dochází periodicky u každé buňky ke kontrole stavu okolních buněk. Těmto
buňkám se řík...
ODORATOR
 upraveny pomocí přiložené korekční tabulky. Pro linearizování přístroje v
jeho měřícím rozsahu je proto přístroj doplněn korekční tabulkou. Do
tabulky vložte obě načtené hodnoty přístroje ODORATOR ...
upraveny pomocí přiložené korekční tabulky. Pro linearizování přístroje v
jeho měřícím rozsahu je proto přístroj doplněn korekční tabulkou. Do
tabulky vložte obě načtené hodnoty přístroje ODORATOR ...
PREPRESS: Vytvoření digitálních dat
 Upravili jsme nastavení “Vzorkování” na “Bikubické
převzorkování na” (1) námi zadané hodnoty.
Barevné obrazy a obrazy ve stupních šedi na 300dpi
pro barevné a 1200dpi pro monochromatické obrazy.
Ty...
Upravili jsme nastavení “Vzorkování” na “Bikubické
převzorkování na” (1) námi zadané hodnoty.
Barevné obrazy a obrazy ve stupních šedi na 300dpi
pro barevné a 1200dpi pro monochromatické obrazy.
Ty...
Jak na data
 Upravili jsme nastavení “Vzorkování” na “Bikubické
převzorkování na” (1) námi zadané hodnoty.
Barevné obrazy a obrazy ve stupních šedi na 300dpi
pro barevné a 1200dpi pro monochromatické obrazy.
Ty...
Upravili jsme nastavení “Vzorkování” na “Bikubické
převzorkování na” (1) námi zadané hodnoty.
Barevné obrazy a obrazy ve stupních šedi na 300dpi
pro barevné a 1200dpi pro monochromatické obrazy.
Ty...
15. Goniometrické funkce
 Je zřejmé, že vzdálenost bodů AB je stejná jako bodů CD. Abychom se nemuseli trápit
s odmocninou ve vzorci o vzdálenosti bodů, budeme pracovat s její druhou mocninou.
Je zřejmé, že vzdálenost bodů AB je stejná jako bodů CD. Abychom se nemuseli trápit
s odmocninou ve vzorci o vzdálenosti bodů, budeme pracovat s její druhou mocninou.
příspěvek
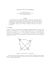 Obrázek 3: K důkazu tvrzenı́ (5)
ve čtyřúhelnı́ku, a tyto úhly mohou být nekonvexnı́. Sinus nekonvexnı́ho úhlu je záporný, což
odpovı́dá odečtenı́ obsahů uvedených trojúhelnı́ků. P...
Obrázek 3: K důkazu tvrzenı́ (5)
ve čtyřúhelnı́ku, a tyto úhly mohou být nekonvexnı́. Sinus nekonvexnı́ho úhlu je záporný, což
odpovı́dá odečtenı́ obsahů uvedených trojúhelnı́ků. P...
Kolik je iracionálních čísel
 otázkám dal aº Georg Cantor v 70. letech 19. století, který mj. ukázal, jak porovnávat nekone£né mnoºiny a ºe existují nekone£na r·zných °ád·. Bliº²í popis t¥chto jist¥ kromoby£ejn¥
zajímavých part...
otázkám dal aº Georg Cantor v 70. letech 19. století, který mj. ukázal, jak porovnávat nekone£né mnoºiny a ºe existují nekone£na r·zných °ád·. Bliº²í popis t¥chto jist¥ kromoby£ejn¥
zajímavých part...