Výrazy a jejichj úpravy
Transkript
Projekt "Podpora výuky v cizích jazycích na SPŠT" Výrazy a jejich úpravy MATA1 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem ČR 1 Výrazy a jejich úpravy 1. Výrazy Již ze základní školy víme, že pro mocniny platí: a ∙ a a 1 Za předpokladu, že a je reálné číslo a r,s jsou čísla přirozená. Co však vzorec (1) znamená? Vždyť se v něm nevyskytuje žádné konkrétní číslo a přesto říkáme, že je to pravidlo pro počítání s mocninami. Tento vzorec popisuje celou řadu početních výkonů, které se řídí stejným pravidlem; znamená např., že 5 ∙ 5 5 , ∙ , π ∙ π π atd. Písmeno a ve vzorci (1) zastupuje libovolné reálné číslo, písmena r, s libovolná přirozená čísla. Takovým písmenům, která v daném zápisu zastupují čísla z určité číselné množiny, říkáme proměnné. Oborem proměnné a je ve vzorci (1) množina všech nenulových reálných čísel, oborem proměnných r, s je množina všech celých čísel. Domluvíme se na tom, že v případech, kdy obor proměnné nebude uveden nebo nebude patrný z textu úlohy, budeme za něj považovat množinu všech reálných čísel takových, pro něž má smysl za proměnné dosazovat. S celou řadou vzorců podobných vzorci (1) jste pracovali již dříve v geometrii, fyzice, chemii a budete s nimi pracovat i v odborných předmětech. V geometrii jsou to např. vzorce: 2r ……………………… vzorec pro výpočet obvodu kružnice …………………….(2) c √a b …………….….. vzorec pro výpočet předpony pravoúhlého trojúhelníka….(3) v πr v …………................ vzorec pro výpočet objemu kužele………………………..(4) V těchto vzorcích jsou proměnné o, r, a, b, c, v, V. Jejich oborem je množina všech kladných reálných čísel (víte, že číselná hodnota obvodu, poloměru, délky strany v trojúhelníku, objemu, výšky může být jen kladné reálné číslo). Ve vzorcích (2) a (4) je písmeno π, které jsme neoznačili jako proměnnou. Toto písmeno totiž – na rozdíl od ostatních písmen v těchto vzorcích – nezastupuje libovolné číslo z určitého oboru, ale jedno určité číslo ( = 3,14…). Taková písmena, která nahrazují určitá čísla, nazýváme konstanty. 2 Terms and their modifications 1. Terms We´ve already known from primary school that for power function stands: a ∙ a a 1 Providing that a is a real number and r, s are numbers nonnegative. What does the formula (1) mean though? Well, there´s no concrete number and despite it is said that the rule for calculating with power functions. The formula describes whole scale of numerical functions that works according to the same rule, e.g. it means that 5 ∙ 5 5 , ∙ , π ∙ π π etc. The letter a substitute any real number in the formula (1). Numbers r, s are arbitrary nonnegative numbers. These numbers which substitute numbers from particular numerical are called variable. The zone of the paramterer a is the set of nonzero real numbers in the formula (1), the zones of the parametres r, s is the set of all integral numbers. It is dealt that if the zone of parametre is not mentioned or is not known from the text of a task, the zone will be taken as the set of all real numbers which can be appointed there instead of it. You have worked with many formulas similar to the formula (1) earlier in geometry, physic, chemistry and you will work with them even in professional subjects. In geometry, e.g. they are formulas: 2r ………… the formula for th.e calculation of icumference ……….....................(2) c √a b ……. the formula for the calculation of hypotenuse of a right triangle……….(3) v πr v ………...the formula for the calculation of the volume of a cone…………….(4) There are variables o,r,a,b,c,v,V in these formulas. Their zone is a set of all positive real numbers (you know the numeric figure of circumference, diameter, the lenght of a side of a triangle, content, hight can be only a positive real number). There is a number, which we didn´t mark as a variable, π in formulas (2) and (4) This number, in fact - in contrast to the other letters in these formulas - didn´t substitute any number of the particular range, but just a single particular number (π = 3,14....). These letters that substitute particular numbers are called constants. 3 Ve vzorcích (2), (3), (4), se vyskytují výrazy 2r ,√a b , v πr v. Na základní škole jste se domluvili, že za výraz budete považovat každý zápis, který je správně utvořen podle dohod o zápisech čísel, proměnných, výsledků operací a hodnot funkcí. S tímto vymezením vystačíme i v této kapitole. Jinak slovo výraz používáme často i v širším slova smyslu než jsme si vymezili na základní škole. Probíráme-li teorii množin, pak např. pracujeme s výrazem ( ∪ ) ∩ C apod. " Výrazy, v nichž se vyskytovala pouze reálná čísla, např. 2, 3, 11, 3 4 , , √ , jste nazývali číselné výrazy. Výrazy, ve kterých se vyskytuje alespoň jedna proměnná, např. 4# , 5$ % 3&$ , # ∙ # 3 , , ' () (*+ , ,)*√() ( , jste nazývali výrazy s proměnou. Ty výrazy, ve kterých je proměnná ve jmenovateli, jste někdy nazývali lomené výrazy. Z () předcházejících příkladů jsou lomené výrazy např. výrazy ' , (*+ . U lomených výrazů nebo u výrazů, v nichž je proměnná pod odmocninou apod., musíme vždy udat takové podmínky pro proměnnou, aby výraz měl smysl (tzn. definiční obor výrazu). Tak např. () ( má smysl jedině za předpokladu - . 0, protože zlomky se jmenovatelem nula nejsou definovány. Výraz √- % 1, má smysl pouze za předpokladu - 0 1, protože druhá odmocnina je definována pouze pro nezáporná reálná čísla. Mezi jednotlivými výrazy, se kterými jste se již setkali, byly i mnohočleny. Mnohočleny jsou např. výrazy 2# % 3# 2, 3# 5# 2# % # 3, 5# % # 1 .Obecně bychom si mohli mnohočlen s jednou proměnou (viz předcházející příklady) definovat následujícím způsobem. Mnohočlen n-tého stupně o proměnné x je výraz -1 # 1 -1* # 1* ⋯ . - # - # -4 , kde # je proměnná, -6 jsou konstanty, n je celé nezáporné číslo a -1 . . Číslo n udává stupeň mnohočlenů. Tak např. 3# 7 % 4# 5# 2# % # 3 je mnohočlen pátého stupně o proměnné x; 5# % # 2 je mnohočlen šestého stupně o proměnné x. Podle počtu nenulových členů mnohočlenu mluvíme o jednočlenu 3# , dvojčlenu 2# % 2 , trojčlenu 7 3# 7 % 4# % apod., mnohočleny mohou obsahovat i více proměnných např. 2# $ % 2#$ % #$ 5# % 3,6# $ % 5#$ 9 5#$ % 3# 39 2 , kde x, y, z jsou proměnné. 4 Terms occure in these formulas (2), (3), (4)2r ,√a b , v πr v. At primary school you made a deal that every notation will be regarded as a term that is made correctly according to the agreement about number notations, variables, the results of operations and the values of functions. This definition are convenient even for this chapter. Alias the word “term” is often used in wider meaning than it was define at primary school. If we discuss the theory of sets, the we work with term e.g: ( ∪ ) ∩ C etc. : √ ,.... Terms in which just real numbers occured, e.g. 2,3,11,3 4 , , numeric terms. were called The terms where at least one variable occures, e.g. 4# , 5$ % 3&$ , # ∙ # 3 , , ' () (*+ , ,)*√() ( , are called terms with varible. The terms in which variable is in a denominator are called frictional terms. Frictional terms are from the previous () examples, for instance: ' , (*+ At frictioanl terms or terms in which variable is rooted etc., we must state such conditions for variable in order to a term has a sense (it means the domain of definition). For instance () ( it has a sense only for providing - . 0, because fricitons with zero denominator are not defined. The term √- % 1, has the sense only for providing - 0 1, because square root is defined only for negative real numbers. Multinominals were among the other terms you have already met. Multinominals are for instance terms 2# % 3# 2, 3# 5# 2# % # 3, 5# % # 1 . In general, multinominals with one variable (vide the previous examples) can be defined by following way. The multinominal n-th grade of variable x is the term -1 # 1 -1* # 1* ⋯ . - # - # -4 , where the variable is x, -6 is a constant, n is an integral non-negative number -1 . . The number n denotes the grade of multinominals. For instance, 3# 7 % 4# 5# 2# % # 3 is the multinominal of the fifth grade of x variable; 5# % # 2 is the multinominal of the sixth grade of variable x. According to the number of the nonzero terms of a multinominal it is defined as a monomial,3# , binomial, 2# % 2 , trinomial 3# 7 % 7 4# % etc., mononominals can contain even more variables, e.g. 2# $ % 2#$ % #$ 5# % 3,6# $ % 5#$ 9 5#$ % 3# 39 2 , where x, y, z are variables. 5 Cvičení 1. Zapište pomocí proměnné x : a) součet trojnásobku libovolného čísla a čísla 2; b) trojnásobek součtu libovolného čísla a čísla 2; c) druhou mocninu součtu dvojnásobku libovolného čísla a čísla 8; d) třetí odmocninu rozdílu libovolného čísla a trojnásobku čísla 6. 2. Zapište pomocí proměnné n v oboru celých čísel : a) libovolné sudé číslo; b) libovolné liché číslo; c) součet dvou sudých čísel za sebou bezprostředně následujících; d) součin dvou sudých čísel za sebou bezprostředně následujících; e) součet dvou lichých čísel za sebou bezprostředně následujících; f) součin dvou lichých čísel za sebou bezprostředně následujících; 3. Zapište výrazy; a) součet druhých mocnin proměnných a, b; b) druhá mocnina součtu proměnných a, b; c) k proměnné x přičtu číslo 4 a výsledek násobím číslem, které je o 4 menší než daná proměnná; k tomu součtu přičtu 15 a výsledek dělíme číslem o 1menší než je daná proměnná. 4. Udejte, kdy mají smysl následující výrazy: a) *' ' ' d) '* '* b) ' ; c) '* f) √# % 7 e) ' ; g) √# 3 6 Exercise 1. Write down with variable x: a) three times the sum of any number a number 2; b) triple the sum fo any number a number 2; c) the square power of the sum of double any number and number 8; d) the cube root of the difference any number and triple the sum fo number 6. 2. Write down with variable n in integers a) any even number; b) any odd number; c) the sum of two even consecutive numbers; d) the product of two even consecutive numbers; e) the sum of two odd consecutive numbers; f) the product of two odd consecutive numbers; 3. Write down terms: a) the sum of the square power of a, b; b) the square power of the sum of variable a, b; c) add 4 to variable x and the result times by the number which is lesser of 4 than the variable; to the sum add 14 and the result divide by the number lesser of 1 than is the variable. 4. Indicate when the following terms have sense: a) *' ' ' d) '* '* b) ' ; c) '* f) √# % 7 e) ' ; g) √# 3 7 2. Počítání s mnohočleny Nejdřív obrátíme svoji pozornost na zopakování operací s mnohočleny. Připomeňme si na několika příkladech, jak se mnoho členy sčítají, odčítají, násobí a jak se dělí mnohočlen jednočlenem. Příklad 1 Sečti mnohočleny 2- = 3-= 5- 7=, 7a 3b 3a = - = . Řešení: 2- = 3-= 5- 7= 7- 3= 3- = - = 2- = - = 3-= 5- 7- 7= 3= 3- = 3- = 3-= 12- 10= 3- = Příklad 2 Od mnohočlenu - = % >odečtěte mnohočlen – = % 3> . Řešení: - = % > — A%= % 3> B - = % > = % 3> - = % > = % 3> - 2= % 4> Příklad 3 7 Násobte mnohočlen # % #$ % jednočlenem %24#$ . Řešení: 3 1 5 3 1 5 C # % #$ % D ∙ %24#$ # ∙ %24#$ % #$ ∙ %24#$ % ∙ %24#$ 4 6 3 4 6 3 %18# $ 4# $ 40#$ 8 2. Calculation with multinominals First of all we focuse on the revision of multinominals. Let´s remain them on a few examples how to sum, subtract and multiplying them, and how to divide a multinominal by a mononominal. Example 1 Sum the multinominals2- = 3-= 5- 7=, 7a 3b 3a = - = . Solution: 2- = 3-= 5- 7= 7- 3= 3- = - = 2- = - = 3-= 5- 7- 7= 3= 3- = 3- = 3-= 12- 10= 3- = Example 2 Substract a mononominal - = % >from a multinominal – = % 3> . Solution: - = % > — A%= % 3> B - = % > = % 3> - = % > = % 3> - 2= % 4> Example 3 7 Multiple a multionominal # % #$ % by a mononominal %24#$ . Solution: 3 1 5 3 1 5 C # % #$ % D ∙ %24#$ # ∙ %24#$ % #$ ∙ %24#$ % ∙ %24#$ 4 6 3 4 6 3 %18# $ 4# $ 40#$ 9 Příklad 4 Násobte mnohočleny 2- 3- = =, - 2= . Řešení: 2- 3- = = ∙ - 2= 2- ∙ - 3- = ∙ - = ∙ - 2- ∙ 2= 3- = ∙ 2= = ∙ 2= 2- 3- = - = 4-= 6- = 2= Příklad 5 Dělte mnohočleny 18- % 27- % 9- % 90- jednočlenem 9- . Řešení: Dělení má smysl za předpokladu - . 0 18- % 27- % 9- % 90- G 9- A18- G 9-B A%27- G 9-B A9- G 9-B A%90- G 9-B 2- % 3- - % 10 Při násobení mnohočlenu jste se na základní škole naučili pro zkrácení výpočtů počítat se vzorci H I H 2HI I , H % I H % 2HI I , ve kterých písmena A, B představovala obvykle jednočleny. V následujících dvou příkladech si zopakujeme počítání podle těchto vzorců. Příklad 6 Vypočítejte 2# . Řešení: J 2# 2 ∙ ∙ 2# 2# 6# 4# 10 Example 4 Multiple a multionominal 2- 3- = =, - 2= . Solution: 2- 3- = = ∙ - 2= 2- ∙ - 3- = ∙ - = ∙ - 2- ∙ 2= 3- = ∙ 2= = ∙ 2= 2- 3- = - = 4-= 6- = 2= Example 5 Divide multionominals 18- % 27- % 9- % 90- by a mononominal 9- . Solution: Division has sense providing that - . 0 18- % 27- % 9- % 90- G 9- A18- G 9-B A%27- G 9-B A9- G 9-B A%90- G 9-B 2- % 3- - % 10 You learn to calculate for cutting calculations with formulas at multiplying a multinominal at primary school H I H 2HI I , H % I H % 2HI I , in which the letters A, B usually represent mononominals. In the following two examples we revise calculation according to these formulas. Example 6 Calculate: 2# . Solution: J 2# 2 ∙ ∙ 2# 2# 6# 4# 11 Příklad 7 Vypočítej 2# $ 0,05 . Řešení: 2# $ 3,05 2# $ % 2 ∙ 2# $ ∙ 0,05 0,05 4# $ 0,2# $ 0,0025 Dále si odvodíme vzorce pro výpočet třetí mocniny dvojčlenů H I, H % I H I H I ∙ H I H 2HI I ∙ H I H 2H I HI H I 2HI I K H 3H I 3HI I H % I H % I ∙ H % I H % 2HI I ∙ H % I H % 2H I HI % I 2HI % I K H % 3H I 3HI % I Platí tedy: H I H 3H I 3HI I H % I H % 3H I 3HI % I V dalších příkladech si počítání podle těchto vzorců procvičíme. Příklad 8 Vypočítejte0,2-= 10$ . Řešení: 0,2-= 10$ 0,2-= 30,2-= ∙ 10$ 3 ∙ 0,2-= ∙ 10$ 10$ 0,008- = 1,2- = $ 60-=$ 100$ Příklad 9 Vypočítejte 2# $ % 9 . 12 Example 7 Calculate: 2# $ 0,05 . Solution: 2# $ 3,05 2# $ % 2 ∙ 2# $ ∙ 0,05 0,05 4# $ 0,2# $ 0,0025 Furthemore we deducate the formulas for the calcutaion of the cubical power of binominals H I, H % I H I H I ∙ H I H 2HI I ∙ H I H 2H I HI H I 2HI I K H 3H I 3HI I H % I H % I ∙ H % I H % 2HI I ∙ H % I H % 2H I HI % I 2HI % I K H % 3H I 3HI % I It is valid that: L M N LN NLO M NLMO MN L % M N LN % NLO M NLMO % MN In the further examples we practise calculating with these formulas. Example 8 Calculate0,2-= 10$ . Solution: 0,2-= 10$ 0,2-= 30,2-= ∙ 10$ 3 ∙ 0,2-= ∙ 10$ 10$ 0,008- = 1,2- = $ 60-=$ 100$ Example 9 Calculate 2# $ % 9 . 13 Řešení: 2# $ % 9 2# $ % 32# $ ∙ 9 3 ∙ 2# $ ∙ 9 % 9 8# $ % 12# $ 9 6# $9 % 9 Cvičení 1. Vypočítejte: a) - = % > = % - > % > % - % = b) - % = % = > % P = > % P 2- % = c) 9- % 8- = 5-= % 7= 7- 2- = 9-= % 11= 2. Násobte: a) %5- 3-= % 8= %9-= b) -= % > % => P >- = =P % - c) Q % $ Q % R QRQ R d) 2# % - # 7 e) # % 3# % 7 # % 2 f) - % 1 - % 2 - 3 % - g) 4# % 3# 2 3# 2# % 1 # % 2# 3 3. Vypočítejte: a) 3# % 5 A3# % 5 3# % 5B b) 3# % 5 A3# % 53# % 5 B c) 3# % 5A3# % 53# % 5 B d) 3# % 5A3# % 5 3# % 5B 14 Solution: 2# $ % 9 2# $ % 32# $ ∙ 9 3 ∙ 2# $ ∙ 9 % 9 8# $ % 12# $ 9 6# $9 % 9 Exercise 1. Calculate: a) - = % > = % - > % > % - % = b) - % = % = > % P = > % P 2- % = c) 9- % 8- = 5-= % 7= 7- 2- = 9-= % 11= 2. Multiple: a) %5- 3-= % 8= %9-= b) -= % > % => P >- = =P % - c) Q % $ Q % R QRQ R d) 2# % - # 7 e) # % 3# % 7 # % 2 f) - % 1 - % 2 - 3 % - g) 4# % 3# 2 3# 2# % 1 # % 2# 3 3. Calculate: a) 3# % 5 A3# % 5 3# % 5B b) 3# % 5 A3# % 53# % 5 B c) 3# % 5A3# % 53# % 5 B d) 3# % 5A3# % 5 3# % 5B 15 4. Dělte (a nezapomeňte udat, kdy má dělení smysl): a) 15- = % 12- = % 9- = 6- = G 3-= b) 8# $ % 6# $ 4# $ % 2# $ G %2# $ c) 4- = % 16- = 8- = % 4-7 = 7 G 8- = d) c) 3# 9# % # 15# % 21# G %9# 5. Vypočtěte s využitím probraných vzorců: a) - % b) 0,2 % 3# c)S– # 2$T d) 2# % 5$ e) 0,1 % 0,2# f) # % $ g) 3# 2$ 3# % 2$ %8# $ h) - > = P %-P -= 3. Dělení mnohočlenů mnohočleny Dělit mnohočlen jednočlenem už umíte; zbývá ještě naučit se dělit mnohočlen mnohočlenem. Pro potřeby střední školy stačí se omezit na mnohočleny s jednou proměnnou. Při dělení mnohočlenu mnohočlenem postupujeme podle návodu, který je popsán v následujícím příkladu. Příklad 10 Vypočtěte 20- 32- 7- % 5- G %1 7- . Řešení: Postupujeme podle tohoto návodu: 16 4. Divide (and don´t forget indicate when the division has sense): a) 15- = % 12- = % 9- = 6- = G 3-= b) 8# $ % 6# $ 4# $ % 2# $ G %2# $ c) 4- = % 16- = 8- = % 4-7 = 7 G 8- = d) 3# 9# % # 15# % 21# G %9# 5. Calculate with using the learnt formulas: a) - % b) 0,2 % 3# d) 2# % 5$ e) 0,1 % 0,2# c)S– # 2$T f) # % $ g) 3# 2$ 3# % 2$ %8# $ h) - > = P %-P -= 3. Division of multinominals by multinominals You can divide. It remains to learn to divide a multinominal by a multinominal. It is enough to know the calculations with one variable for needs of secondary school. We proceed at dividing a multinominal by a mononominal according to the instruction which is described in the following example. Example 10 Calculate: 20- 32- 7- % 5- G %1 7- . Solution: We proceed according to the instruction: 17 1. Oba mnohočleny uspořádáme sestupně podle klesajících mocnin proměnné a: 7- 20- 32- % 5- G 7- % 1 2. Dělíme: a) První člen dělence dělíme prvním členem dělitele 7- G 7- - . Získaný podílem - násobíme všechny členy dělitele, tj. 7- % 1 ∙ - 7- % - . Tento dílčí výsledek odečteme od dělence. Zápis: 7- 20- 32- % 5- G 7- % 1 - %7- % - 21- 32- % 5- b) Postup opakujeme, a to tak, že prvním členem dělitele dělíme první člen zbytku, který je uspořádán sestupně 21- G 7- 3- . Získaným podílem 3- násobíme dělitele, tj. 7- % 1 ∙ 3- 21- % 3- a tento další dílčí výsledek odečteme od zbytku. Zápis: 7- 20- 32- % 5- G 7- % 1 - 3- %7- % - 21- 32- % 5%21- % 3- 35- % 5c) Opět zopakujme postup z předcházejících dvou kroků, tj. 35- G 7- 5- ,7- % 1 ∙ 5- 35- % 5- a tento dílčí výsledek odečteme od zbytku. 18 1. Both multinominal are ordered in descending order according to the decreasing powers of variable a: 7- 20- 32- % 5- G 7- % 1 2. Divide a) The first term of a dividend divide by the first term of a divider 7- G 7- - By the gained fraction is multiplied all terms of a divider, it means 7- % 1 ∙ - 7- % - This partial result substract from dividend. Note: 7- 20- 32- % 5- G 7- % 1 - %7- % - 21- 32- % 5b) We repeat the process and the way that we divide the first term of division remainder by the first term of divider, 21- G 7- 3- . We multiply obtained quotient byadivisor3- 7- % 1 ∙ 3- 21- % 3- and this partial result substract from the remainder. Note: 7- 20- 32- % 5- G 7- % 1 - 3- %7- % - 21- 32- % 5%21- % 3- 35- % 5c) Again we repeat the process from the previous two steps, it means 35- G 7- 5-, 7- % 1 ∙ 5- 35- % 5- and the partial result substract from the remainder. 19 Zápis: 7- 20- 32- % 5- G 7- % 1 - 3- +5a %7- % - -. Z 21- % 3- % 5%21- % 3- 35- % 5%35- % 5- 0 3. O správnosti výsledku se můžeme přesvědčit zkouškou, kdy zjistíme, zda součin dělitele a podílu je roven dělenci: - 3- 5- 7- % 1 7- 21- 35- % - % 3- % 5 7- 20- 32- % 5- Příklad 11 Vypočtěte 2# 11# % 5# % 24 G 2# % 3 . Řešení: 2# 11# % 5# % 24 G 2# % 3 # 7# 8 %2# % 3# #. 14# % 5# % 24 - 14# % 21# 16# % 24 -16# % 24 0 20 Note: 7- 20- 32- % 5- G 7- % 1 - 3- +5a %7- % - -. Z 21- % 3- % 5%21- % 3- 35- % 5%35- % 5- 0 3. We can persuade about the result by the test in which we figure out if the product of divider and the fraction is equal to a dividend: - 3- 5- 7- % 1 7- 21- 35- % - % 3- % 5 7- 20- 32- % 5- Example 11 Calculate: 2# 11# % 5# % 24 G 2# % 3 . Solution: 2# 11# % 5# % 24 G 2# % 3 # 7# 8 %2# % 3# #. 14# % 5# % 24 - 14# % 21# 16# % 24 -16# % 24 0 21 Výsledek: 2# 11# % 5# % 24 G 2# % 3 # 7# 8 , # . Zkouška: # 7# 8 2# % 3 2# 14# 16# % 3# % 21# % 24 2# 11# % 5# % 24 Příklad 12 Vypočtěte 10#4 % 15# J 27# Z % 3# 2# 7 3# 5# % 5# G 2x % 3x 5 . Řešení: 10#4 % 15# J 27# Z % 3# 2# 7 3# 5# % 5# G 2x % 3x 5 5# Z # # % # %10#4 % 15# J 25# Z 2# % 3# 5 . 0 2# Z % 3# 2# 7 3# 5# % 5# %2# Z % 3# 5# 2# 7 % 5# 3# 5# % 5# 2# 7 % 3# % 5# %2# 3# % 5# %%2# 3# % 5# 0 Výsledek: 10#4 % 15# J 27# Z % 3# 2# 7 3# 5# % 5# G 2x % 3x 5 5# Z # # % # , 2x % 3x 5 . 0 22 The result 2# 11# % 5# % 24 G 2# % 3 # 7# 8 , # . Test: # 7# 8 2# % 3 2# 14# 16# % 3# % 21# % 24 2# 11# % 5# % 24 Example 12 Calculate: 10#4 % 15# J 27# Z % 3# 2# 7 3# 5# % 5# G 2x % 3x 5 . Solution: 10#4 % 15# J 27# Z % 3# 2# 7 3# 5# % 5# G 2x % 3x 5 5# Z # # % # %10#4 % 15# J 25# Z 2# % 3# 5 . 0 2# Z % 3# 2# 7 3# 5# % 5# %2# Z % 3# 5# 2# 7 % 5# 3# 5# % 5# 2# 7 % 3# % 5# %2# 3# % 5# %%2# 3# % 5# 0 The result: 10#4 % 15# J 27# Z % 3# 2# 7 3# 5# % 5# G 2x % 3x 5 5# Z # # % # , 2x % 3x 5 . 0 23 Zkouška: 2# % 3# 5 5# Z # # % # 10#4 % 15# J 25# Z 2# Z % 3# 5# 2# 7 % 3# 5# % 2# 3# % 5# 10#4 % 15# J 27# Z % 3# 2# 7 3# % 5# % 5# Příklad 13 Vypočtěte 21# % 31# 39# % 6 : 7# % 1 . Řešení: 21# % 31# 39# % 6 : 7# % 1 3# % 4# 5 %21# % 31# %28# 39# % 6 %%28# 4# 35# % 6 %35# % 5 %1 Jednočlen -1 (tj. - 1# 4 ) má nižší stupeň než mnohočlen 7# % 1. Proto v dělení dále pokračujeme. Mnohočlen 3# % 4# 5 se nazývá částečný podíl, jednočlen -1 se nazývá zbytek. Výsledek: 21# % 31# 39# % 6 G 7# % 1 3# % 4# 5 % Z'* 7# % 1 . 0 24 Test: 2# % 3# 5 5# Z # # % # 10#4 % 15# J 25# Z 2# Z % 3# 5# 2# 7 % 3# 5# % 2# 3# % 5# 10#4 % 15# J 27# Z % 3# 2# 7 3# % 5# % 5# Example 13 Calculate: 21# % 31# 39# % 6 : 7# % 1 . Solution: 21# % 31# 39# % 6 : 7# % 1 3# % 4# 5 %21# % 31# %28# 39# % 6 %%28# 4# 35# % 6 %35# % 5 %1 The mononominal -1(it is - 1# 4 ) has lower lever than mononominal7# % 1. Therefore we continue in division. A multinominal 3# % 4# 5 is called a partional fraction, a mononominal - 1 is called a reminder. The result: 21# % 31# 39# % 6 G 7# % 1 3# % 4# 5 % 7# % 1 . 0 25 Z'* Zkouška: C3# % 4# 5 % 1 1 D 7# % 1 3# % 4# 5 7# % 1 % ∙ 7# % 1 7# % 1 7# % 1 21# % 28# 35# % 3# 4# % 5 % 1 21# % 31# 39# % 6 Příklad 14 Dělte 14# 7 4# % # 2# 3# 5 G 2# % 1 . Řešení: 14# 7 4# % # 2# 3# 5 G 2# % 1 7# 2# 3# 2 %14# 7 % 7# #. √ , #.% √ 4# 6# 2# 3# 5 %4# % 2# 6# 4# 3# 5 %6# % 3# 4# 6# 5 %4# % 2 6# 7 Výsledek: 14# 7 4# % # 2# 3# 5 G 2# % 1 7# 2# 3# 2 'Z ' ; * Zkouška: 7# 2# 3# 2 'Z ' ; * 'Z 2# % 1 7# 2# 3# 2 2# % 1 ' ; * 2# % 1 14# 7 4# % # 2# 3# 5 26 ;#.] √ Test: C3# % 4# 5 % 1 1 D 7# % 1 3# % 4# 5 7# % 1 % ∙ 7# % 1 7# % 1 7# % 1 21# % 28# 35# % 3# 4# % 5 % 1 21# % 31# 39# % 6 Example 14 Divide: 14# 7 4# % # 2# 3# 5 G 2# % 1 . 14# 7 4# % # 2# 3# 5 G 2# % 1 7# 2# 3# 2 %14# 7 % 7# #. √ , #.% √ 4# 6# 2# 3# 5 %4# % 2# 6# 4# 3# 5 %6# % 3# 4# 6# 5 %4# % 2 6# 7 The result 14# 7 4# % # 2# 3# 5 G 2# % 1 7# 2# 3# 2 'Z ' ; * Test: 7# 2# 3# 2 'Z ' ; * 'Z 2# % 1 7# 2# 3# 2 2# % 1 ' ; * 2# % 1 14# 7 4# % # 2# 3# 5 27 ;#.] √ Cvičení 1. Vypočítejte: a) - 3- 3- 1 G - 1 b) 4# 4# % 29# G 2# % 3 c) -7 % 8- 24- 32- 26 G - % 1 2. Vypočítejte: a) 3- - 11 G - 8- b) # 2 G # 1 c) # ( % 7# % 9 G # % 2 d) -7 % 3- 5 G - % 1 4. Rozklad pomocí vytýkání Ze základní školy umíte najít společný násobek a společného dělitele dvou či více celých čísel. Znalost určování společného násobku celých čísel využíváme např. při sčítání zlomků. Tak při sčítání 7 5 1 12 6 24 je nutné určit jejich společného jmenovatele. Tím může být např. číslo 1 728 jako součin jednotlivých jmenovatelů 12. 6. 24. Protože si však jistě nechce komplikovat výpočet zbytečně velkými čísly, zvolte jako společný jmenovatel číslo 24, které je nejvhodnějším společným násobkem těchto tří čísel. 28 Exercise: 1. Calculate a) - 3- 3- 1 G - 1 b) 4# 4# % 29# G 2# % 3 c) -7 % 8- 24- 32- 26 G - % 1 2. Calculate a) 3- - 11 G - 8- b) # 2 G # 1 c) # ( % 7# % 9 G # % 2 d) -7 % 3- 5 G - % 1 4. Factorizing by means of determining You are already able to find the common multiple and the common divisor of two or more integral numbers from primary school. We imply the knowledge of determining of the common multiple of integral numbers for e.g. the adding of frictions 7 5 1 12 6 24 it is necessary to find a common denominator . That number can be e.g. 1 728 as the product of single denominators 12. 6. 24. As nobody wants to complicate calculation with uselessly large numbers, the best choice is to choose the number 24 as a common denominator because is the most appropriate common multiple of these numbers. 29 Při hledání rozkladu daného výrazů v součin používáme různé druhy úprav. Jednou z nich je vytýkání společného činitele z daného výrazu. Máme např. rozložit v součin výraz 22-= 28- = 14- = . Protože 22-= 2-= ∙ 11=, 28- = 2-= ∙ 14-=, 14- = 2-= ∙ 7- , je nejvhodnějším společným dělitelem těchto tří sčítanců výraz 2ab. Je tedy 22-= 28- = 14- = 2-= ∙ 11= 2-= ∙ 14-= 2-= ∙ 7- . Po vytknutí výrazu 2ab dostaneme původní výraz ve tvaru součinu dvou výrazů 2-=11= 14-= 7- . Platí tedy 22-= 28- = 14- = 2-=11= 14-= 7- . Příklad 15 Rozložte v součinu výraz 18- % 45- 63- . Řešení: Protože nejvhodnějším společný dělitel všech tří sčítanců je jednočlen 9-, platí 18- % 45- 63- 9-2 % 5- 7- V následujícím příkladu si ukážeme dva postupy při počítání s výrazy; jednak bez rozkladu výrazu v součin, jednak s rozkladem výrazu v součin. Sami posuďte, který z nich je namáhavější a zdlouhavější. Příklad 16 Vypočtěte povrch válce o průměru 24 mm a výšce 9 mm. 30 We use various modifications in looking for the factorizing of the given term. One of them is the decomposition of the common factor from the given term. E.g. we are supposed to factorize a term 22-= 28- = 14- = . Because 22-= 2-= ∙ 11=, 28- = 2-= ∙ 14-=, 14- = 2-= ∙ 7- , is the most appropriate common divisor these three tots the term 2ab. 22-= 28- = 14- = 2-= ∙ 11= 2-= ∙ 14-= 2-= ∙ 7- . After factorizing the term 2ab we get the original term as the product of two terms. 2-=11= 14-= 7- . So it is valid 22-= 28- = 14- = 2-=11= 14-= 7- . Example 15 Factorize the term 18- % 45- 63- . Solution: Because the most appropriate common divisor of all three tots is an monomial 9-, it is given: 18- % 45- 63- 9-2 % 5- 7- Two examples about calculating with terms are shown in the following example; the one without factorizing of the term in a product and the other with factorizing of the temr in a product. Make a judgement yourselves which of the two terms is more affordable and tedious. Example 16 Calculate the surface of a cylinder with the diameter of 24 mm and the length of 9 mm. 31 Řešení: 1. způsob: dosazeni do vzorce ^ 2_ 2_R dostaneme: ^ 2 ∙ 3,14 ∙ 12 2 ∙ 3,14 ∙ 12 ∙ 9 `` 2 ∙ 3,14 ∙ 144 3,14 ∙ 12 ∙ 18 `` 6,28 ∙ 144 3,14 ∙ 216 `` 904,32 678,24 `` 1582,56`` ≐ 1,583`` 2. Způsob: upravíme-li vzorec ^ 2_ 2_R na tvar ^ 2__ R , je numerický výpočet jednodušší: ^ 2 ∙ 3,14 ∙ 12 ∙ 12 9 `` 3,14 ∙ 24 ∙ 21`` 3,14 ∙ 504`` 1582,56`` ≐ 1583`` Vytýkání společného násobku ze všech členů výrazu je pouze jedním z možných způsobů, jak rozložit výraz v součinu. Např. úlohu rozložit v součin výraz 5=$ 15= # 4-$ 12-=# tímto způsobem nevyřešíme (můžeme vytknout pouze 1nebo -1). Zkusíme, zda lze tento výraz rozložit jiným způsobem. Můžeme si např. všimnout, že první dva členy mají společného dělitele 5=, poslední dva 4-. Vytkneme: 5=$ 3=# 4-$ 3=# Po této úpravě jsme dostali dva sčítance, jejichž společným dělitelem je výraz $ 3=# , který vytkneme $ 3=# 5= 4- Dostali jsme tedy: 5=$ 15= # 4-$ 12-=# $ 3=# 5= 4- Tomuto způsobu rozkladu výrazu v součin říkáme postupné vytýkání. 32 Solution: 1. way: it is given by a substitution to the pattern: ^ 2_ 2_R: ^ 2 ∙ 3,14 ∙ 12 2 ∙ 3,14 ∙ 12 ∙ 9 `` 2 ∙ 3,14 ∙ 144 3,14 ∙ 12 ∙ 18 `` 6,28 ∙ 144 3,14 ∙ 216 `` 904,32 678,24 `` 1582,56`` ≐ 1,583`` 2. way: if we adjust the term ^ 2_ 2_R to the shape ^ 2__ R , the numerical calculation is easier: ^ 2 ∙ 3,14 ∙ 12 ∙ 12 9 `` 3,14 ∙ 24 ∙ 21`` 3,14 ∙ 504`` 1582,56`` ≐ 1583`` The prefixing of the common pultiple from all terms is merely one of possible multiples how to factorize the rerm in the product. For instance, a rider factorize the product the term: 5=$ 15= # 4-$ 12-=# by this way it is not possible to solve the rider (we can prefix only 1 or -1). We try whether this term can be factorized by another way. We can realize the first two terms have a common divider 5=, we factorize the last two 4-. We factor out: 5=$ 3=# 4-$ 3=# After the conversion two addend appeared whose common divider is the term $ 3=# , which is prefixed $ 3=# 5= 4- We were given: 5=$ 15= # 4-$ 12-=# $ 3=# 5= 4- This kind of factorizing the product is called progressive factorizing. 33 Příklad 17 Rozložte v součinu výraz b$ 7$ % b$ % 7# . Řešení: Zdůvodněte jednotlivé kroky v následujícím výpočtu: b$ 7$ % b$ % 7# b# % b$ 7$ % 7# b# % $ 7$ % # b# % $ 7%1 %$ # b# % $ % 7# % $ # % $ b % 7 Dostáváme tak: b# % 7$ % b$ % 7# # % $ b % 7 Zkouška: # % $ b % 7 b# % b$ 7# 7$ Příklad 18 Rozložte v součin výraz # - % = # % -=. Řešení: # - % = # % -= # -# % =# % -= ## - % =# - # - # % = Zkouška: # - # % = # -# % =# % -= # - % = # % -= 34 Example 17 Factorize the product the term b$ 7$ % b$ % 7# . Solution: Give reasons for each step in the following calculation: b$ 7$ % b$ % 7# b# % b$ 7$ % 7# b# % $ 7$ % # b# % $ 7%1 %$ # b# % $ % 7# % $ # % $ b % 7 As we were given: b# % 7$ % b$ % 7# # % $ b % 7 Test: # % $ b % 7 b# % b$ 7# 7$ Example 18 Factorize the product # - % = # % -=. Solution: # - % = # % -= # -# % =# % -= ## - % =# - # - # % = Test: # - # % = # -# % =# % -= # - % = # % -= 35 Cvičení 1. Rozložte v součin: a) - = -= b) 6- = % 3- = c) # 7 % # d) 15-7 = % 30- = J 2. Rozložte v součin: a) 32-= # % 48- =# 64-= # b) 33` R % 27`R 24` R 3. Rozložte v součin: a) - % = 9- 9= b) - 2-= = % > c) 2- % 3= % 3= % 2- d) 2# 7 % # $ % #$ 4. Rozložte v součin: a) #$ 2 2$ 2 b) -= % 2 % 3= % 2 c) >b % c b % c d) 2#3# 1 % 3# % 1 e) `# % $ % # $ f) 4-- % = % - = 5. Rozklad výrazů pomocí vzorců Dalším z možných postupů, které lze při rozkladu výrazů v součin použít, je rozklad pomocí vzorců. Zatím známe vzorce : H I H 2HI I H % I H % 2HI I 36 Exercises: 1. Factorize the product: a) - = -= b) 6- = % 3- = c) # 7 % # d) 15-7 = % 30- = J 2. Factorize the product: a) 32-= # % 48- =# 64-= # b) 33` R % 27`R 24` R 3. Factorize the product: a) - % = 9- 9= b) - 2-= = % > c) 2- % 3= % 3= % 2- d) 2# 7 % # $ % #$ 4. Factorize the product: a) #$ 2 2$ 2 b) -= % 2 % 3= % 2 c) >b % c b % c d) 2#3# 1 % 3# % 1 e) `# % $ % # $ f) 4-- % = % - = 5. Factorizing the terms in terms of formulas Another of the likely consecutions, in which factorizing the product is able to use, is factorizing in terms of formulas. Already known formulas: H I H 2HI I H % I H % 2HI I 37 H % I H % I H I H I H 3H I 3HI I H % I H % 3H I 3HI % I Doplníme si tyto vzorce ještě dalšími: H I H I H % HI I H % I H % I H HI I O jejich správnosti se můžeme přesvědčit vynásobením mnohočlenů na pravých stranách. Příklad 19 Rozložte v součin # % J . Řešení: Použijeme vzorec H % I H % I H I , v němž položíme H #, I . Dostaneme: # % 1 1 1 C# % D C# D 9 3 3 Příklad 20 Rozložte v součin 9- % 12-= 4= . Řešení: Užitím vzorce H % 2HI I H % I , kde H 3- , I 2= , dostaneme: 9- % 12-= 4= 3- % 2 ∙ 3- ∙ 2= 2= 3- % 2= 38 H % I H % I H I H I H 3H I 3HI I H % I H % 3H I 3HI % I We add more formulas: H I H I H % HI I H % I H % I H HI I We can check their correctness by multiplying of the multinominals on the right sides. Example 19 Factorize the product: # % J . Solution: We use the formula H % I H % I H I , in which put H #, I . We are given: # % 1 1 1 C# % D C# D 9 3 3 Example 20 Factorize the product: 9- % 12-= 4= . Solution: Using the formula H % 2HI I H % I , where H 3- , I 2= , it is given: 9- % 12-= 4= 3- % 2 ∙ 3- ∙ 2= 2= 3- % 2= 39 Příklad 21 Rozložte v součin 0,25# $ % # % 2 . Řešení: Ze vzorce H % I = H % I H I ,kde H 0,5#$ , I #– 2 , máme:, 0,25# $ - #– 2 A0,5#$ % # % 2 B A0,5#$ # % 2 B 0,5#$ % # 2 0,5#$ # % 2 Příklad 22 Rozložte v součin # 6# $ 12#$ 8$ . Řešení: Použijeme vzorec H 3H I 3HI I H I , kde H #, I 2$, a dostaneme: # 6# $ 12#$ 8$ # 3 ∙ # ∙ 2$ 3 ∙ # ∙ 2$ 2$ = (x+2y Příklad 23 Rozložte v součin 27 – 8# $ . Řešení: K rozkladu použijeme vzorec H % I H % I H HI I , dPeH 3, I 2#$ : 27-8# $ 3 % 2#$ A3 3 ∙ 2#$ 2#$ B= =(3- 2x$ 9 6#$ 4# $ 40 Example 21 Factorize the product: 0,25# $ % # % 2 . Solution: From the formule H % I = H % I H I ,where H 0,5#$ , I #– 2 , we have, 0,25# $ - #– 2 A0,5#$ % # % 2 B A0,5#$ # % 2 B 0,5#$ % # 2 0,5#$ # % 2 Example 22 Factorize the product: # 6# $ 12#$ 8$ . Solution: we use formula where H 3H I 3HI I H I , where H #, I 2$and we are given: # 6# $ 12#$ 8$ # 3 ∙ # ∙ 2$ 3 ∙ # ∙ 2$ 2$ = (x+2y Example 23 Factorize the product 27 – 8# $ . Solution: We use the formule for factorozing H % I H % I H HI I , fge_eH 3, I 2#$ : 27-8# $ 3 % 2#$ A3 3 ∙ 2#$ 2#$ B= =(3- 2x$ 9 6#$ 4# $ 41 Příklad 24 Rozložte v součin 81# % $ . Řešení: Použijeme vzorec H % I H % I H I , dPeH 9# , I $ . 81# % $ 9# % $ 9# $ Použijeme-li na dvojčlen 9# % $ 3# % $ znovu vzorec pro Rozdíl druhých mocnin, dostáváme: 81# % $ 9# % $ 9# $ 3# % $ 3# $ 9# $ Cvičení 1. Rozložte v součin : a) # % 4- b) 36# $ % 1 c) # $ % 16 d) - = % = e) - = % 4-= f) g % 1 g) # % # h) b % c % _ 2. Rozložte v součin : a) 4# % 4#$ $ b) 9= % 12=> 4> c) # 2-#$ - $ d) # % 1 % 3# 3# e) 89 27h 36h9 54h 9 Literatura:doc. RNDr. Emil Calda a kolektiv:Matematika pro střední odborné školy a studijní obory středních odborných učilišť, 1. část 42 Example 24 Factorize the product 81# % $ . Solution We use th formula H % I H % I H I , fge_eH 9# , I $ . 81# % $ 9# % $ 9# $ If we use for the binomial 9# % $ 3# % $ the formula again for the division of square power is: 81# % $ 9# % $ 9# $ 3# % $ 3# $ 9# $ Exercises: 1. Factorize the product: a) # % 4- b) 36# $ % 1 c) # $ % 16 d) - = % = e) - = % 4-= f) g % 1 g) # % # h) b % c % _ 2. Factorize the product: a) 4# % 4#$ $ b) 9= % 12=> 4> c) # 2-#$ - $ d) # % 1 % 3# 3# e) 89 27h 36h9 54h 9 Literatura:doc. RNDr. Emil Calda a kolektiv:Matematika pro střední odborné školy a studijní obory středních odborných učilišť, 1. část 43
Podobné dokumenty
05 经济 - 经济观察报
 Lk !%#' %(=ô2m
å^
jºoM : !%#' %l !%!( %
rTqHI\](0
ãcKF©z:3HI$
qA`Ý`ÇûÂÀî :jk
\](v@ i$º2
HÂi(89MÿL!Ç(T
UVW)*@M%~%rY%©
Å@:3HI:jk\](
qM2.H(Ø
~å^`(ØM$J
2M ...
Lk !%#' %(=ô2m
å^
jºoM : !%#' %l !%!( %
rTqHI\](0
ãcKF©z:3HI$
qA`Ý`ÇûÂÀî :jk
\](v@ i$º2
HÂi(89MÿL!Ç(T
UVW)*@M%~%rY%©
Å@:3HI:jk\](
qM2.H(Ø
~å^`(ØM$J
2M ...
Bezdiskové stanice na Ubuntu Linuxu
 Po aktualizaci zdrojů balíčků nainstalujte balíčky openoffice.org a openclipart. První
nainstaluje samotný OpenOffice a druhý galerii obrázků OpenClipart.
Po aktualizaci zdrojů balíčků nainstalujte balíčky openoffice.org a openclipart. První
nainstaluje samotný OpenOffice a druhý galerii obrázků OpenClipart.
TLAČ 3/2010
 Už 18. ročník populárního festivalu Benátská noc v Malé Skále
na Turnovsku naplnil veškerá očekávání. Přitáhl několik zahraničních hvězd i hvězdiček, představil českou i slovenskou špičku
od A do...
Už 18. ročník populárního festivalu Benátská noc v Malé Skále
na Turnovsku naplnil veškerá očekávání. Přitáhl několik zahraničních hvězd i hvězdiček, představil českou i slovenskou špičku
od A do...
Metodika matematiky - Základní škola Cheb
 musíme vložit velké úsilí např. do osvojení slovní zásoby, tak si musíme trvale uchovat
některé matematické informace (např. součiny v násobilce). Počítače a kalkulačky jsou jen
pomocníkem – nenahr...
musíme vložit velké úsilí např. do osvojení slovní zásoby, tak si musíme trvale uchovat
některé matematické informace (např. součiny v násobilce). Počítače a kalkulačky jsou jen
pomocníkem – nenahr...
4/6 Vyčíslování redox rovnic
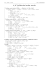 ∙ u I je 5 ⇒ 5I2 , 10I – I , u Mn je 2 ⇒ 2MnO4 – , 2Mn2+
∙ kyslíky na levé straně: 2 · 4 = 8 ⇒ 8H2 O ⇒ 16H+
∙ náboje: L : 2− + 10− + 16+ = 4+ ; P : 2 · 2+ = 4+ ⇒ L = P
∙ 2MnO4 – + 10I – + 16H+
2Mn2...
∙ u I je 5 ⇒ 5I2 , 10I – I , u Mn je 2 ⇒ 2MnO4 – , 2Mn2+
∙ kyslíky na levé straně: 2 · 4 = 8 ⇒ 8H2 O ⇒ 16H+
∙ náboje: L : 2− + 10− + 16+ = 4+ ; P : 2 · 2+ = 4+ ⇒ L = P
∙ 2MnO4 – + 10I – + 16H+
2Mn2...
zde - Základní škola Opava
 kartičky, dá je na hromádku textem dolů. Je stanoven určitý časový limit, např. jedna minuta.
Žák začne vysvětlovat slovo anglicky. Např. na kartičce je slovo „football.“ Žák opisem
vysvětlí toto s...
kartičky, dá je na hromádku textem dolů. Je stanoven určitý časový limit, např. jedna minuta.
Žák začne vysvětlovat slovo anglicky. Např. na kartičce je slovo „football.“ Žák opisem
vysvětlí toto s...
český jazyk - ZŠ při DPN, Louny
 - umí vyznačit stavbu slov a pojmenovat jednotlivé části
- slova odvozená
- uvádí k jednotlivým slovům slova základová
- slova příbuzná
- vyloží význam odvozených slov
- vyznačí slovotvorné základy...
- umí vyznačit stavbu slov a pojmenovat jednotlivé části
- slova odvozená
- uvádí k jednotlivým slovům slova základová
- slova příbuzná
- vyloží význam odvozených slov
- vyznačí slovotvorné základy...