3.Teorie pružnosti a pevnosti
Transkript
Obsah
1
Úvod do předmětu Pružnost a pevnost
. . . . . . . . . . . . . . . . . .
1
1.1
Cíl PP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.2
Návaznosti . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.3
Přístupy PP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.4
Základní pojmy pružnosti a pevnosti . . . . . . . . . . . . . . . . .
3
Mezní stavy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.1
Mezní stav deformace . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.2
Mezní stav pružnosti . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.3
Mezní stav deformační stability . . . . . . . . . . . . . . . . . . . .
7
2.4
Mezní stav porušení . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2
3
Prvek tělesa a napětí v řezu
. . . . . . . . . . . . . . . . . . . . . . . .
10
3.1
Princip určování napětí . . . . . . . . . . . . . . . . . . . . . . . . .
11
3.2
Přehled modelových těles řešitelných analyticky . . . . . . . . . . .
11
3.3
Rozdělení PP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
Napjatost v bodě tělesa . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
Saint Venantův princip . . . . . . . . . . . . . . . . . . . . . . . . .
15
5
Deformace těles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
6
Zatížení tělesa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
7
Základní formulace lineární PP . . . . . . . . . . . . . . . . . . . . . . .
23
Hookův zákon . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
Obecný Hookův zákon . . . . . . . . . . . . . . . . . . . . . . .
24
7.2
Práce síly při deformaci tělesa . . . . . . . . . . . . . . . . . . . . .
25
7.3
Obecné věty lineární pružnosti . . . . . . . . . . . . . . . . . . . . .
26
7.3.1
Věta o superpozici . . . . . . . . . . . . . . . . . . . . . . . . .
26
7.3.2
Věta o vzájemnosti prací (Bettiho věta) . . . . . . . . . . . . .
26
7.3.3
Deformační práce soustavy osamělých sil . . . . . . . . . . . . .
28
7.3.4
Věta Castiglianova . . . . . . . . . . . . . . . . . . . . . . . . .
29
8
Základní vlastnosti pružně plastického materiálu . . . . . . . . . . . . .
32
9
Tahová a tlaková zkouška . . . . . . . . . . . . . . . . . . . . . . . . . .
33
Tahová zkouška materiálu v houževnatém stavu . . . . . . . . . . .
33
9.1.1
Oblast pružných deformací (I) . . . . . . . . . . . . . . . . . .
33
9.1.2
Oblast rovnoměrných pružně plastických deformací (II)
34
4
4.1
7.1
7.1.1
9.1
I
. . . .
9.1.3
Oblast nerovnoměrných pružně plastických deformací (III) . . .
34
9.2
Tlaková zkouška materiálu v houževnatém stavu . . . . . . . . . . .
34
9.3
Tahová a tlaková zkouška materiálu v křehkém stavu . . . . . . . .
35
Prut v pružnosti a pevnosti . . . . . . . . . . . . . . . . . . . . . . . . .
36
10
10.1
Prutové předpoklady . . . . . . . . . . . . . . . . . . . . . . . . . .
36
10.2
Geometrické charakteristiky příčného průřezu . . . . . . . . . . . .
38
10.2.1
Plocha příčného průřezu . . . . . . . . . . . . . . . . . . . . . .
38
10.2.2
Lineární (statické) momenty . . . . . . . . . . . . . . . . . . . .
38
10.2.3
Kvadratické momenty . . . . . . . . . . . . . . . . . . . . . . .
38
10.2.4
Základní vlastnosti kvadratických momentů průřezu . . . . . .
39
10.2.5
Kvadratické momenty základních tvarů průřezů . . . . . . . . .
39
10.2.6
Kvadratické momenty průřezu při transformaci souřadnic . . .
40
10.2.7
Hlavní kvadratické momenty . . . . . . . . . . . . . . . . . . .
40
10.2.8
Mohrova kružnice kvadratických momentů . . . . . . . . . . . .
41
10.3
Výsledné vnitřní účinky prutů (VVÚ) . . . . . . . . . . . . . . . . .
41
10.4
Určování VVÚ . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
11
10.4.1
Přístupy k řešení průběhů VVÚ . . . . . . . . . . . . . . . . . .
44
10.4.2
Pomocná pravidla pro vyšetřování průběhu VVÚ u přímých prutů 46
10.4.3
Otevřené vázané pruty . . . . . . . . . . . . . . . . . . . . . . .
47
10.4.4
Uzavřené pruty - rámy . . . . . . . . . . . . . . . . . . . . . . .
51
10.4.5
Algoritmus určování VVÚ . . . . . . . . . . . . . . . . . . . . .
51
Prostý tah a tlak . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
53
11.1
Definice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
53
11.2
Geometrické vztahy . . . . . . . . . . . . . . . . . . . . . . . . . . .
53
11.3
Rozložení napětí v příčném průřezu . . . . . . . . . . . . . . . . . .
54
11.4
Závislost mezi VVÚ a napětím . . . . . . . . . . . . . . . . . . . . .
54
11.5
Extrémní napětí . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
55
11.6
Energie napjatosti . . . . . . . . . . . . . . . . . . . . . . . . . . .
55
11.7
Vyjádření deformační charakteristiky střednice . . . . . . . . . . . .
56
11.8
Deformace příčného průřezu . . . . . . . . . . . . . . . . . . . . . .
56
11.9
Rozbor napjatosti prostého tahu . . . . . . . . . . . . . . . . . . . .
57
11.9.1
11.10
Grafické znázornění napjatosti . . . . . . . . . . . . . . . . . .
58
Oblasti použitelnosti prostého tahu prutů . . . . . . . . . . . . . . .
59
11.10.1
Vliv proměnnosti průřezu podél střednice prutu . . . . . . . . .
60
11.10.2
Vliv šroubovitosti prutu . . . . . . . . . . . . . . . . . . . . . .
61
11.10.3
Proměnnost VVÚ podél střednice přímého prutu . . . . . . . .
62
11.10.4
Zakřivení střednice prutu . . . . . . . . . . . . . . . . . . . . .
63
II
11.11
12
13
Řešení úlohy PP u prutů namáhaných prostým tahem (tlakem) . .
64
11.11.1
Volný prut . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
64
11.11.2
Vázaný prut . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
11.11.3
Soustavy s pruty namáhanými prostým tahem (tlakem) . . . .
66
Prostý krut . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71
12.1
Definice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71
12.2
Geometrické vztahy . . . . . . . . . . . . . . . . . . . . . . . . . . .
71
12.3
Rozložení napětí v příčném průřezu . . . . . . . . . . . . . . . . . .
72
12.4
Závislost mezi VVÚ a napětím . . . . . . . . . . . . . . . . . . . . .
73
12.5
Extrémní napětí . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
12.6
Energie napjatosti . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
12.7
Vyjádření deformační charakteristiky střednice . . . . . . . . . . . .
74
12.8
Deformace příčného průřezu . . . . . . . . . . . . . . . . . . . . . .
75
12.9
Řešení úlohy PP u prutů namáhaných krutem . . . . . . . . . . . .
75
12.9.1
Volný prut . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
75
12.9.2
Vázaný prut . . . . . . . . . . . . . . . . . . . . . . . . . . . .
76
Prostý ohyb . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
78
13.1
Definice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
78
13.2
Geometrické vztahy . . . . . . . . . . . . . . . . . . . . . . . . . . .
78
13.3
Rozložení napětí v příčném průřezu . . . . . . . . . . . . . . . . . .
79
13.4
Závislost mezi VVÚ a napětím . . . . . . . . . . . . . . . . . . . . .
79
13.5
Extrémní napětí . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
80
13.6
Energie napjatosti . . . . . . . . . . . . . . . . . . . . . . . . . . .
81
13.7
Vyjádření deformačních charakteristik střednice . . . . . . . . . . .
82
13.8
Deformace příčného průřezu . . . . . . . . . . . . . . . . . . . . . .
83
13.9
Oblasti použitelnosti prostého ohybu prutů . . . . . . . . . . . . . .
84
13.9.1
Vliv proměnnosti průřezu podél střednice prutu . . . . . . . . .
84
13.9.2
Proměnnost ohybového momentu podél střednice . . . . . . . .
84
13.9.3
Zakřivení střednice prutu . . . . . . . . . . . . . . . . . . . . .
86
Řešení úlohy PP u prutů namáhaných ohybem . . . . . . . . . . . .
87
13.10
13.10.1
Volný prut . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
87
13.10.2
Diferenciální přístup . . . . . . . . . . . . . . . . . . . . . . . .
87
13.10.3
Integrální přístup . . . . . . . . . . . . . . . . . . . . . . . . . .
88
13.10.4
Porovnání diferenciálního a integrálního přístupu . . . . . . . .
88
13.10.5
Vázaný prut . . . . . . . . . . . . . . . . . . . . . . . . . . . .
89
14
Zakřivené a lomené otevřené pruty . . . . . . . . . . . . . . . . . . . . .
90
15
Vzpěrná stabilita prutů . . . . . . . . . . . . . . . . . . . . . . . . . . .
92
III
15.1
Vzpěrná stabilita ideálního volného prutu . . . . . . . . . . . . . .
92
15.2
Kritická síla vzpěru u vázaného prutu . . . . . . . . . . . . . . . . .
95
15.3
Tlakové namáhání prutu ze skutečného materiálu . . . . . . . . . .
96
Matematický popis napjatosti . . . . . . . . . . . . . . . . . . . . . . .
98
16
16.1
Hlavní souřadnicový systém . . . . . . . . . . . . . . . . . . . . . .
98
16.2
Určení napětí v obecné rovině . . . . . . . . . . . . . . . . . . . . .
99
16.3
Napětí v oktaedrické rovině . . . . . . . . . . . . . . . . . . . . . .
99
16.4
Grafické znázornění napjatosti . . . . . . . . . . . . . . . . . . . . . 100
16.5
Zvláštní typy napjatosti . . . . . . . . . . . . . . . . . . . . . . . . 100
17
16.5.1
Trojosá (prostorová) napjatost . . . . . . . . . . . . . . . . . . 100
16.5.2
Dvojosá (rovinná) napjatost . . . . . . . . . . . . . . . . . . . . 101
16.5.3
Jednoosá (přímková) napjatost . . . . . . . . . . . . . . . . . . 102
16.5.4
Nulová napjatost . . . . . . . . . . . . . . . . . . . . . . . . . . 102
Úvod do nauky o mezních stavech . . . . . . . . . . . . . . . . . . . . . 103
17.1
Součinitel bezpečnosti . . . . . . . . . . . . . . . . . . . . . . . . . 103
17.2
Mezní stav pružnosti . . . . . . . . . . . . . . . . . . . . . . . . . . 104
17.2.1
Podmínka plasticity max τ (Trescova) . . . . . . . . . . . . . . 105
17.2.2
Podmínka plasticity HMH (Misesova) . . . . . . . . . . . . . . 107
17.3
Obecná a prostá bezpečnost . . . . . . . . . . . . . . . . . . . . . . 108
18
Metoda konečných prvků . . . . . . . . . . . . . . . . . . . . . . . . . . 110
19
Nomogramy součinitelů koncentrace napětí . . . . . . . . . . . . . . . . 113
s01
Základy statiky nutné pro PP . . . . . . . . . . . . . . . . . . . . . . . 120
Použitá literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 132
IV
1. Úvod do předmětu Pružnost a pevnost
Pružnost a pevnost (PP), jako jedna ze základních součástí mechaniky těles, patří
k základním oborům strojního inženýrství. Není náhodou, že při zakládání prvních
technických vysokých škol v 19. století byla obvykle hlavní náplní studia, i když častěji
zaměřená na oblast stavebního inženýrství. Již tehdy se začala projevovat potřeba
zajištění bezpečné, spolehlivé a bezporuchové funkce konstruovaných zařízení, která
se stávala hnací silou rozvoje inženýrství a vedla k vymezení PP jako samostatného
oboru.
Tato dlouhá tradice má jako každá mince dvě strany. Na straně jedné je nesporný význam pružnosti a pevnosti pro všechny strojírenské obory, protože neexistuje žádný,
který by se nepotýkal se zmíněným problémem zajištění funkčnosti. Za rub této mince
lze považovat například fakt, že tradiční název oboru Pružnost a pevnost je dnes již
zavádějící, neboť tento obor za více než století své samostatné existence prošel několika
zásadními změnami. V dobách, kdy tento název vznikl, měl zřejmě vyjadřovat hlavní
náplň oboru, kterou bylo určování pružných deformací a posuzování pevnosti – odolnosti proti porušování. S rozvojem techniky se stále více užívají materiály, které nejsou
pružné, dokonce i tradiční materiály jako ocel jsou nasazovány v takových oblastech
použití (zatížení, teploty, atd.), kdy jejich deformace není pouze pružná. K velké většině
porušení součástí dochází únavou materiálu, jež představuje složitý proces, začínající
změnami v mikrostruktuře materiálu, které se následně projeví vznikem trhliny, a pokračující jejím růstem až do lomu součásti. Tento proces popisuje lomová mechanika
a samozřejmě již nevystačí s jedinou charakteristikou zvanou mez pevnosti (pevnost),
tak jako problematiku deformací nelze zjednodušovat na pojem pružnost už jen proto,
že ke ztrátě funkčnosti vedou daleko častěji deformace, které pružné nejsou.
Současnou náplní oboru, z tradice nazývaného Pružnost a pevnost, je tedy
deformačně-napěťová analýza těles a nauka o mezních stavech. V detailněj- mezní stav na
ším členění a přístupech vychází tento interaktivní studijní text ze skripta [1], které str. 5
přizpůsobuje potřebám a nárokům bakalářského studijního programu a kombinované
formy studia.
1.1. Cíl PP
Cílem PP je zabránit ztrátě funkčnosti součástí, zařízení a konstrukcí způsobené nadměrnou deformací a porušováním, případně rekonstruovat příčiny, proč k této ztrátě
funkčnosti došlo před uplynutím požadované doby jejich životnosti.
Pružnost a pevnost ve strojním inženýrství pomáhá konstruktérovi stanovit rozměry
a tvar strojních součástí a konstrukcí s ohledem na bezpečnost, životnost, ekonomiku,
případně se zohledněním dalších aspektů (estetický vzhled, ekologie, ergonomie atd.).
Základní úlohu PP lze pak formulovat jako analýzu vlivu zatížení tělesa na jeho
deformaci a napjatost s ohledem na riziko vzniku mezních stavů.
Naší snahou musí být zajistit provozuschopnost navrhovaných zařízení, tj. minimalizovat nepříznivé následky případných mezních stavů, anebo naopak procesů souvisejících
se vznikem jednotlivých mezních stavů v praxi účelně využívat (např. technologické
operace tváření, založené na plastické deformaci, nebo dělení materiálu, využívající
1
procesy porušování). Přitom musíme formulovat a řešit problémy pružnosti a pevnosti
a tvůrčím způsobem uplatňovat znalosti získané při řešení úloh PP.
Základní rozdíl mezi úlohou PP a problémem PP je tedy následující:
– úloha PP je naformulovaná zadavatelem a její řešení je víceméně rutinní (procvičuje nebo ověřuje zvládnutí výpočetních postupů);
– problém PP musí řešitel někdy sám formulovat, musí získat informace potřebné
pro jeho řešení a při řešení pak tvůrčím způsobem uplatnit znalosti a zkušenosti
osvojené při řešení úloh, případně jiných problémů.
Z pochopitelných důvodů jsou náplní studia výhradně úlohy PP, pokud možno ovšem
doplněné o základní informace o praktických problémech PP, při jejichž řešení lze
osvojené postupy využít.
1.2. Návaznosti
V následujícím neúplném schématu je znázorněno zařazení oboru pružnost a pevnost
do kontextu ostatních vědních oborů:
Vědy o přírodě a společnosti
(
((( ((((
(
(
((
(((
(
(
+
(
(
hhh
HH
hhhh
hhh
H
hhh
H
hhh
H
h
h
H
fyzika
matematika
termodynamika
filosofie
hhh
H XXX
hhh
HH XXX
h
XX hhhhhh
H
X
hhh
HH
XX
j
hhh
XX
h
X
optika
mechanika
(
((( (((
(
(
(
((((
((((
tekutin
akustika
hhh
h
hhh
sypkých látek
hhhh
aa
aa hhhhhh
hhhh
aa
hhh
aa
hh
pružnost a pevnost
elektřina
hhh
hhhh
h
těles
((( (((
(
(
((
((((
(
(
((
(
+
statika
hhh
biologie
XX
XX
XXX
deformačně-napěťová analýza
kinematika
dynamika
XX
XX
X
nauka o mezních stavech
1.3. Přístupy PP
a) Intuitivní – navrhování způsobu řešení na základě znalostí a zkušeností, bez
schopnosti exaktního zdůvodnění jeho správnosti nebo optimálnosti. Tento přístup je u konstruktéra primární a důležitý, ale rozhodně ne postačující. Jedině
intuitivně je možné vybrat z obrovského množství možných variant taková řešení, která rozumně přicházejí v úvahu, ale musí být následně posouzena jinými
přístupy.
2
b) Výpočtový – založený na vytvoření výpočtového modelu, tedy zavedení takových
zjednodušení, která na jedné straně umožní popis reality dostupnými matematickými prostředky a na druhé straně zajistí přijatelnou shodu s realitou.
Výpočtové modely
– analytické – teorie prutů, skořepin, desek, . . .
– numerické – metoda konečných prvků, metoda hraničních prvků, . . .
c) Experimentální - experimenty lze provádět na reálném objektu nebo na jeho
materiálním modelu. Nevýhodou experimentů na reálném objektu je ekonomická
i časová náročnost, některé experimenty nejsou ani možné (atomové elektrárny, letadla) nebo jsou natolik drahé, že se k nim přistupuje až po důkladném výpočtovém
modelování (bariérová zkouška automobilů). Experiment na modelu vyžaduje zase
existenci vhodných měřicích metod a zařízení pro jejich realizaci a dále splnění jistých kriterií, zajišťujících přenositelnost výsledků na dílo (např. vodní turbíny).
Experiment je nezbytný pro jakékoliv výpočtové modelování, pro které zajišťuje
vstupní údaje (např. vlastnosti materiálů) a rovněž slouží verifikaci výsledků.
1.4. Základní pojmy pružnosti a pevnosti
Obor PP používá řadu pojmů, jejichž přesné vymezení je základem pochopení všech
jevů, procesů a souvislostí, jimiž se budeme zabývat. Jednotné chápání obsahu těchto
pojmů je základním předpokladem tvůrčího inženýrského přístupu, který je v moderním pojetí paralelního inženýrství založen na neustálé průběžné komunikaci mezi
konstruktérem, technologem, výpočtářem, případně dalšími specialisty (designér, ekolog,. . . ).
Mechanický pohyb – byl definován v předmětu Statika, která se však zabývala pouze
pohybem tuhého tělesa jako celku. Mechanický pohyb tělesa má však i další složky,
důležité zejména z hlediska PP.
Složky mechanického pohybu
a) pohyb tělesa jako celku,
b) deformace,
c) porušování.
V některých případech je nesnadné jednoznačně oddělit pohyb tělesa jako celku od
jeho deformace (např. bariérová zkouška automobilů). V základním kurzu PP se však
budeme zabývat pouze tělesy, která se vůči základnímu tělesu nepohybují (s výjimkou
případné rovnoměrné rotace kolem pevné osy). Základní těleso předpokládáme spojené s inerciální soustavou, jinak bychom museli ke skutečným vnějším silám přidat
i zdánlivé (setrvačné) síly. (To je nutné např. tehdy, je-li zvoleným základním tělesem vozidlo při průjezdu zatáčkou, brzdění či rozjezdu.) Abychom deformaci, která je deformace
v tomto případě jedinou složkou pohybu tělesa, mohli určovat metodami statické PP, str. 18
musí být všechny síly v čase konstantní. Deformace sice může vést až k porušení tělesa,
ale samotným průběhem procesu porušování už se v našem kurzu detailně zabývat
nebudeme.
Těleso reálné a teoretické
Základním prvkem mechanické soustavy je reálné těleso. Pro řešení mu přiřazujeme
výpočtový model, tj. těleso teoretické, které má vlastnosti:
– spojité,
– spojitě deformovatelné až do mezního stavu porušení,
3
na
rozlišovací úroveň
– geometrie je určena na technické rozlišovací úrovni ,
– vlastnosti materiálu jsou určeny materiálovými charakteristikami,
– shoduje se s reálným tělesem pouze ve vlastnostech podstatných pro řešení
daného problému.
Podstatné vlastnosti tělesa lze nejlépe osvětlit na příkladu:
ojnice spalovacího motoru je reálné těleso, pro něž lze použít následující úrovně modelu:
– pro řešení sil působících v obou čepech ojnice při zatížení tlakem na píst nám
stačí obecně známá informace o přímé střednici tělesa, jeho vazbách (čepy – rotační vazby) a roztečná vzdálenost obou čepů.
Pak lze výpočtový model znázornit tímto obrázkem:
základní
úloha PP
str. 1
na
– je-li u rychloběžného motoru podstatné i zatížení setrvačnými silami, potřebujeme
znát úplnou geometrii ojnice, její hustotu a parametry jejího pohybu (vektory
rychlosti a zrychlení jednotlivých bodů ojnice),
– pro řešení základní úlohy PP musí výpočtový model navíc zahrnovat elastické
a pevnostní parametry materiálu včetně jejich závislosti na teplotě a samozřejmě
znalosti rozsahu provozních teplot,
– je-li vyšetřovaným tělesem ojnice, pro niž je typické dynamické zatěžování (v čase
proměnné), pak výpočtový model musí zohlednit únavu materiálu, tedy zahrnout
navíc všechny parametry, které ji ovlivňují (jakost povrchu, jeho technologická
úprava – kalení, cementování, válečkování, atd.)
4
2. Mezní stavy
V kapitole 6. Zatížení tělesa jsou mezi různými zatěžovacími stavy zavedeny stavy zatížení
přechodové a mezní jako stavy, v nichž je částečně nebo úplně a dočasně nebo trvale str. 21
znemožněna funkce tělesa (soustavy). Protože rozhodnutí, zda bude zařízení dále provozováno (ať už pouze částečně nebo po opravě) anebo zda bude vyřazeno z provozu,
závisí na mnoha dalších faktorech mimo PP (ekonomika, ergonomie, ekologie atd.),
nebudeme nadále mezi přechodovými a mezními stavy rozlišovat a všechny je budeme
označovat jako stavy mezní. V tomto obecném smyslu lze pak vyslovit následující definici:
Mezní stav je takový ze zatěžovacích stavů tělesa, při němž se kvalitativně mění schopnost tělesa plnit některou z požadovaných funkcí, příp. těleso tuto schopnost zcela ztrácí.
na
Na příkladu oběžného kotouče turbíny si uvedeme některé příklady mezních stavů:
a) došlo k porušení kotouče v průběhu jeho lisování na hřídel nebo za provozu – mezní
stav porušení,
b) vyskytly se nadměrné deformace lopatek dosahující velikosti vůle mezi rotorem
a skříní turbíny – mezní stav deformace,
c) vyskytly se lomy některých lopatek – mezní stav porušení,
d) došlo k uvolnění nalisování kotouče na hřídeli – mezní stav deformace.
Při posuzování mezního stavu konstrukce je třeba brát v úvahu, že se skládá z celé
řady podsoustav a jednotlivých částí. Můžeme vymezit jistý soubor možných mezních
stavů, které jsou pro danou soustavu podstatné. K vyřazení konstrukce z provozu pak
dojde po dosažení alespoň jednoho z nich.
MS porušení na
str. 7
MS deformace
na str. 6
MS porušení na
str. 7
Faktory způsobující nebo ovlivňující vznik mezního stavu, lze členit na vnější
a vnitřní.
a) Vnějšími faktory jsou například:
– mechanické zatížení (stálé, proměnné – statické, dynamické, rázové; důležitá zatížení
je velikost zatížení a jeho časový průběh),
str. 21
– teplotní zatížení,
– prostředí (chemicky neutrální nebo agresivní, ovlivňující povrch nebo objem
materiálu),
– energetická pole (magnetické, elektrické ap.),
– porušení výrobních nebo provozních předpisů,
– chyby v organizaci práce,
– chybná manipulace,
– nesprávné seřízení,
– požár, povodeň aj.
b) Vnitřními faktory jsou především:
– nevhodná volba materiálu (jeho chemického složení, tepelné, chemické nebo
mechanické zpracování),
– vada materiálu nebo svaru,
– nevhodná konstrukce nebo technologie,
– nedodržení kvality výroby, aj.
Úplný a dokonalý popis všech možných mezních stavů konstrukce je velice obtížný.
Mezní stavy mohou být klasifikovány z mnoha různých hledisek. V inženýrské praxi se
nejčastěji setkáváme s následujícími mezními stavy:
5
na
–
–
–
–
mezní
mezní
mezní
mezní
stav
stav
stav
stav
deformace,
pružnosti,
deformační stability,
porušení.
2.1. Mezní stav deformace
Příklad 404
Jednotlivé konstrukční díly se při zatížení deformují, dochází ke změně jejich rozměrů,
tvaru, uložení (vůlí nebo přesahu). Pokud jsou tyto deformace v takových mezích, aby
zařízení pracovalo v souladu se stanovenými technickými podmínkami (vztahujícími se
např. k přesnosti výrobků, pohyblivosti soustavy apod.), mluvíme o funkčně přípustných deformacích.
Například mezi lopatkou turbíny a statorem je vůle v. Z termodynamického hlediska (z důvodu vysoké účinnosti) by bylo vhodné, aby tato
vůle byla co nejmenší, nejlépe v = 0. Pro funkci turbíny je ale důležité, aby součet radiálního posuvu na vnějším obvodě rotoru turbíny ur
a radiálního prodloužení lopatkového listu ∆l byl menší než radiální
mezera v. Může tedy nastat
ur + ∆l < v
ur + ∆l > v
ur + ∆l = v
→ deformace funkčně přípustná,
→ deformace funkčně nepřípustná,
→ mezní stav deformace; rovnost nelze vzhledem ke stochastickému
charakteru všech veličin v praxi zajistit.
Mezní stav deformace tělesa je takový jeho stav, ve kterém se deformace funkčně
přípustné mění na deformace funkčně nepřípustné.
Poznámka: funkčně nepřípustná deformace přitom může být jak elastická, tak plastická.
2.2. Mezní stav pružnosti
Když těleso zatěžujeme z výchozího (nezatíženého) stavu na určitou úroveň zatížení
a pak ho odlehčíme, uskutečníme zatěžovací cyklus. Z praxe víme, že mohou nastat
zásadně dva případy:
a) deformace po odlehčení je tak malá,
že je dostupnými prostředky v oboru nezjistitelná ⇒ celá deformace byla pružná
(vratná) ,
b) deformace po odlehčení je zjistitelná
dostupnými prostředky v oboru ⇒ kromě
pružné vznikla v průběhu zatěžovacího
cyklu i plastická (nevratná, trvalá) deformace.
Mezní stav pružnosti tělesa je takový jeho stav, při jehož překročení vznikají v tělese
zjistitelné plastické deformace.
Mezní stav pružnosti je jedním z nejčastěji používaných mezních stavů: pro materiály
v tvárném stavu je dostatečně konzervativní (poskytuje posouzení na bezpečné straně,
6
ost
tj. součást snese ve skutečnosti vyšší zatížení než výpočtové) a je poměrně výpočtově
nenáročný (je potřebné řešení pouze v pružné oblasti).
2.3. Mezní stav deformační stability
Příklad: Vytahujeme kovový svinovací metr ze schránky. Do určité délky má jistou
geometrickou konfiguraci. Při dalším vytahování dosáhneme délky l, při níž se tato
konfigurace stane nestabilní a pás přejde do jiné stabilní geometrické konfigurace (výrazně se ohne).
Mezní stav deformační stability tělesa je stav, kdy geometrická konfigurace, která
byla stabilní před dosažením mezního stavu, se po jeho překročení stává labilní a stabilní
se stává jiná geometrická konfigurace tělesa.
Tento mezní stav vzniká u konstrukcí, jejichž rozměr je v některém směru podstatně
menší než ve směru jiném (tenkostěnné konstrukce, štíhlé pruty), a to v případě, že
v konstrukci nebo její části vzniknou záporná normálová napětí (tlaková). Pak může
dojít ke ztrátě únosnosti celé konstrukce. Protože tento mezní stav je obvykle spojen
se vznikem velkých deformací, je jeho výpočtové řešení mimořádně obtížné. Mezní
veličina závisí na tvaru konstrukce, v případě prutů namáhaných tlakem je jí kritická
síla vzpěru a mezní stav se pak nazývá mezní stav vzpěrné stability.
normálové
napětí na str. 14
prut na str. 36
vzpěr na str. 92
2.4. Mezní stav porušení
Zatěžujeme-li spojité těleso, můžeme pozorovat, že v určitém rozsahu zatěžování zůstává spojitost tělesa (v mechanickém smyslu, tj. makroskopicky) zachována. Těleso spojitost tělesa
zůstává tedy i při zatížení spojitým. Po překročení tohoto rozsahu zatěžování vznikají na str. 120
poruchy spojitosti (trhliny), přitom se vytvářejí nové povrchy tělesa a proces může
pokračovat tak dlouho, až se těleso rozpadne na více částí – vzniká jeho lom. Je katastrofickým zakončením stádia růstu defektů a dovršením porušení tělesa, které se
tím rozpadá na části. Podle charakteru zatěžujících a ovlivňujících faktorů a chování
materiálu lze rozlišit následující typy lomů:
a) Tvárný lom
Tvárný lom lze z mechanického hlediska definovat jako vysokoenergický plastický
kolaps, ke kterému dochází po vzniku plastické nestability v kritickém průřezu tělesa. Z fyzikálně metalurgického hlediska jde o proces nukleace, růstu a spojování
mikrodutin. Praktický význam je dán tím, že se často uplatňuje v mikroskopickém
měřítku na čele šířící se trhliny [6]. Je třeba se jej vyvarovat u technologických
operací, využívajících velkých plastických deformací (hluboké tažení plechů, drátů,
tváření za studena aj.)
7
b) Křehký lom
Pro vznik křehkého lomu je rozhodující kritická hodnota normálového napětí (u těles bez apriorních trhlin) resp. kritická hodnota hnací síly trhliny (u těles s trhlinami). Tento lom nastává bez větší předchozí plastické deformace, při napětích
nižších než makroskopická mez kluzu materiálu.
– těleso bez apriorních trhlin – důležitou charakteristikou odolnosti materiálu vůči křehkému lomu je kritické lomové napětí σcF , což je nejnižší napětí
nutné pro vznik křehkého lomu.
– těleso s trhlinami – většina křehkých lomů v rozměrných konstrukcích iniciuje z trhlin, které jsou přítomny v materiálu vinou nedokonalé technologie
při výrobě (svary, kalení atd.) nebo vlivem předchozího provozu konstrukce
(korozní trhliny, únavové trhliny). Poněvadž je nutno s existencí těchto defektů
vždy počítat, vzniká otázka, za jakých podmínek může dojít k nestabilnímu
křehkému lomu (tj. trhlina roste i když těleso odlehčíme, tento růst je už člověkem neovlivnitelný). Jednou z nejdůležitější charakteristik odolnosti proti
křehkému lomu je lomová houževnatost, která je určena kritickou hodnotou hnací síly trhliny, odpovídající okamžiku nestabilního lomu.
c) Lom korozí pod napětím
Vliv okolního prostředí může podstatně urychlit poškozovací procesy vedoucí k iniciaci trhlin a jejich šíření. Jedním z nejvýznamnějších degradačních mechanismů
v tomto smyslu je koroze, tj. chemická nebo elektrochemická reakce mezi prostředím a materiálem. Ke stabilnímu šíření trhlin v korozním prostředí dochází
při nižších napětích než v prostředí inertním, kde je stabilní šíření obtížné. Také
lomové houževnatosti je dosaženo při nižších hodnotách zatížení. V souvislosti
s problematikou provozu jaderných elektráren vyvstává do popředí další typ degradačního procesu – poškození materiálu vlivem radioaktivního záření, které
také snižuje hodnotu lomové houževnatosti.
d) Únavový lom
Podrobíme-li součásti působení proměnlivých vnějších sil, může dojít po určité
době k jejich lomu, ačkoliv maximální napětí je pod mezí kluzu. Probíhá proces
postupného porušování materiálu nukleací mikrodefektů a jejich šířením – únava
materiálu. Únavový lom je nejčastějším provozním mezním stavem. K posouzení
únavové pevnosti slouží mez únavy materiálu, k posouzení únavové životnosti
se používá Wöhlerova křivka a Mansonova – Coffinova křivka.
e) Creepový lom
Je-li deformační chování materiálu závislé na čase i při konstantním zatížení, jedná
se o creep (tečení materiálu), který rovněž může vést k lomu při napětím nižším
než je mez pevnosti materiálu. V praxi nejčastěji používanou mezní hodnotou
napětí je mez pevnosti při tečení.
Mezní stav porušení je takový zatěžovací stav tělesa, při kterém dojde k porušení
jeho spojitosti některým z uvedených mechanismů tak, že příslušná konstrukce nemůže
plnit stanovenou funkci.
K vyřazení konstrukce z provozu přitom může dojít:
– z důvodu bezpečnosti při výskytu jakékoliv zjistitelné trhliny (např. svary důležitých tlakových nádob kontrolované rentgenem),
8
– pokud se délka trhliny blíží tzv. kritické délce, při níž nastává její nestabilní
šíření končící nutně lomem,
– pokud trhlina sice nehrozí lomem, ale znemožňuje funkci konstrukce (např. únik
média z tlakové nádoby),
– pokud dojde k lomu součásti.
9
3. Prvek tělesa a napětí v řezu
Asi před 200 lety přišel Bernoulli na geniální myšlenku, že v tělese vznikají vnitřní síly,
které se snaží při vnějším silovém působení na těleso vrátit toto těleso do původního
statická rovno- nedeformovaného stavu. Ve statice jste se seznámili s pojmem statická rovnováha
váha na str. 123 a dospěli jste k závěru: jestliže je těleso ve statické rovnováze, musí být ve statické
rovnováze i každá jeho část. Základním vyšetřovaným objektem – prvkem soustavy
těles bylo těleso. V PP je těleso základním útvarem a prvkem nazýváme každou
jeho část vyšetřovanou z hlediska vnitřních sil.
Prvek tělesa je každá jeho souvislá část, oddělená z něj jedním nebo více myšlenými
řezy. V těchto řezech působí vnitřní síly.
Geometrický tvar prvku volíme s ohledem na tvar vyšetřovaného tělesa, zvolený souřadnicový systém a charakter řešeného problému. Rozměry prvku mohou být buď konečné
nebo nekonečně malé v limitním smyslu.
Prvek označíme jako
síla na str. 120
– konečný (Ω0 ) – všechny rozměry konečné,
– jednonásobně elementární (Ω1 ) – jeden rozměr nekonečně malý,
– dvojnásobně elementární – dva rozměry nekonečně malé,
– trojnásobně elementární (Ω3 ) – tři rozměry
nekonečně malé.
Vyšetřování vnitřních sil začíná uvolněním prvku.
Oddělíme-li z tělesa prvek jediným řezem ω, pak na
tomto řezu musíme zavést účinky vzájemného působení. V mechanice těles to jsou účinky silové, spojitě
nebo po částech spojitě rozložené na řezu a jsou to
tedy plošné síly. Tuto operaci nazýváme uvolněním
prvku tělesa, analogicky k uvolnění celého tělesa,
které jsme zaváděli ve statice a které sloužilo k určení vnějších silových účinků – reakcí ve vazbách.
Na plošku dS v řezu ω působí elementární síla dF~ = f~dS, kde f~ je měrná plošná síla,
kterou nazveme obecné napětí v řezu. Může mít v každém bodě řezu jiný směr
i velikost.
Souřadnicový systém je vhodné při určování vnitřních sil
volit tak, že jedna osa je totožná se směrem normály
k plošce dS a druhá bude ve směru tečném. Normálové
a tečné síly se totiž výrazně liší v účinku na materiál a jejich
vliv na mezní stavy je odlišný.
Obecné napětí f~ rozložíme do směru normály ~en a do směru
tečny ~et :
f~ = σ e~n + τ e~t.
Obecné napětí je vektor, který má samozřejmě v trojrozměrném prostoru 3 složky:
jednu normálovou σ a dvě smykové τ . Při vhodné volbě souřadnicového systému (jedna
10
z os je normála řezu a druhá průsečnice tečné roviny řezu s rovinou danou normálou
~ však je jedno ze smykových napětí (ve směru ~eb ) nulové. Ani při jiné volbě
a vektorem f)
souřadnicového systému není nutné mezi oběma tečnými směry rozlišovat, z hlediska
mezních stavů je důležitá pouze velikost smykového napětí. Pak lze psát
σ = f~ · e~n ,
τ=
q
f 2 − σ 2 = f~ · e~t.
Základní jednotkou napětí (obecného, normálového, smykového) a měrné plošné síly je
pascal.
[f] = [σ] = [τ ] = [dF/dS] = Pa
Určení orientace napětí:
normálového: σ > 0 =⇒ tahové, směřuje ven z řezu,
σ < 0 =⇒ tlakové, směřuje dovnitř prvku,
smykového:
volí se smluvně, u izotropních materiálů není volba podstatná.
orientace
str. 57
na
3.1. Princip určování napětí
Na těleso Ω působí rovnovážná silová soustava Π.
Řezem ω uvolníme prvek Ω01 zatížený podsoustavou Π1 (členy soustavy Π působící v bodech
prvku Ω01 ), která ale už nesplňuje podmínky statické rovnováhy. Protože každý uvolněný prvek musí
být ve statické rovnováze, působí v řezu ω soustava
elementárních vnitřních plošných sil Πv (obecná napětí v bodech řezu) a soustava Π1 ∪ Πv je staticky
rovnovážná.
Rozložení obecného napětí v řezu ω neznáme, vzhledem k elementárnosti sil představuje
nekonečný počet neznámých parametrů a jeho určení je tedy úloha staticky neurčitá.
Použitelné podmínky statické rovnováhy poskytnou pouze ν ≤ 6 rovnic (podle charakteru soustavy Π1 ∪ Πv ), takže pro řešení by byl nutný velký počet deformačních
podmínek.
statický rozbor
na str. 128
statické
podmínky
na
Uvolníme-li při řešení vnitřních sil z tělesa trojnásobně elementární prvek, dosta- str. 123
neme soustavu parciálních diferenciálních rovnic se složitými okrajovými podmínkami. deformační podV předpočítačové éře tato soustava nebyla obecně řešitelná, ale pružnostně – pevnostní mínka na str. 43
problémy bylo nutno řešit. Proto vznikly přístupy, které problém zjednodušovaly zavedením jistých předpokladů, vyplývajících z experimentů a z úrovně vědy v příslušné
době. Zavedení těchto předpokladů sice snižuje náročnost řešení problémů, ale omezuje
použitelnost pouze na ta tělesa, u nichž jsou tyto předpoklady s dostatečnou přesností
splněny. Jde tedy o jednodušší, ale omezeně použitelnou pružnost, pracující s modelovými tělesy [2]. Jejich přehled, který je současně přehledem možností analytické PP,
uvádí kapitola 3.2.
3.2. Přehled modelových těles řešitelných analyticky
Úloha řešení deformačně – napěťových stavů tělesa je analyticky řešitelná pouze při
zavedení jistých předpokladů. Tyto předpoklady vymezují následující typy modelových
těles:
11
1.
2.
3.
4.
5.
6.
prut,
tlustostěnné těleso válcové nebo kulové,
rotačně symetrická stěna,
rotačně symetrická deska,
rotačně symetrická bezmomentová skořepina,
válcová momentová skořepina.
Jak je z přehledu vidět, možnosti analytické pružnosti a pevnosti jsou omezeny kromě
těles prutových na tělesa rotačně symetrická. Rotační symetrie musí být dodržena
nejen z hlediska geometrie, ale i materiálu, vazeb a zatížení tělesa. Jedině potom je
i napjatost a deformace tělesa také rotačně symetrická a lze ji analyticky řešit. Ostatní
tělesa vyžadují numerické řešení s využitím speciálních počítačových metod a programů. Uvedené názvy abstraktních modelových těles se běžně přenášejí i na tělesa
skutečná, o nichž pak hovoříme jako o prutu, skořepině, desce atd. Proto je třeba
zdůraznit, že výpočtový model použitelný pro řešení (a to nejen v pružnosti analytické,
ale i při použití numerických metod) není jednoznačně dán tvarem tělesa, ale závisí i na
okrajových podmínkách, zahrnujících vazby a zatížení tělesa.
prutové předpoklady na str. 36
1. Prut - základním prvkem je jednonásobně elementární prvek, jehož použití
umožňují prutové předpoklady.
2. Tlustostěnné těleso válcové nebo kulové - základním prvkem je trojnásobně
elementární prvek. Praktické využití při výpočtech tlakových nádob.
3. Rotačně symetrická stěna - těleso definované střednicovou rovinou a tloušťkou
(výrazně menší oproti ostatním rozměrům), jehož zatížení leží pouze ve střednicové rovině. V praxi nejčastěji používáno pro výpočet rychloběžných kotoučů zatížených odstředivými silami, případně nalisováním na hřídel. Základním prvkem
je dvojnásobně elementární prvek.
4. Rotačně symetrická deska - těleso definované shodně se stěnou, ale zatížené
pouze kolmo ke střednicové rovině. V praxi používáno pro výpočet přírub, dna
nádob, pístů apod. Základním prvkem je dvojnásobně elementární prvek.
5. Rotačně symetrická bezmomentová skořepina - těleso definované rotační
střednicovou plochou a tloušťkou (výrazně menší oproti ostatním rozměrům), zatížené spojitě bez skokových změn a uložené tak, aby nedocházelo k omezení radiálních posuvů (jsou splněny předpoklady bezmomentovosti). V praxi se používá
pro výpočet většiny rotačně symetrických nádob (včetně trubek) s tím, že v oblastech, kde jsou omezeny radiální posuvy nebo dochází ke skokovým změnám
spojitého zatížení, tato teorie neplatí a napětí mají vyšší hodnoty při složitějším
charakteru napjatosti. Základním prvkem je dvojnásobně elementární prvek.
6. Válcová momentová skořepina - těleso definované válcovou střednicovou plochou a tloušťkou (výrazně menší oproti ostatním rozměrům), které při splnění podmínek rotační symetrie nesplňuje podmínky bezmomentovosti. Základním prvkem
je dvojnásobně elementární prvek.
3.3. Rozdělení PP
napjatost
str. 14
Při silovém působení se prvek deformuje, proto by se měl uvolňovat v deformovaném
stavu, což vede ke značným výpočtovým složitostem, protože tento stav na začátku
výpočtu neznáme. Deformaci a napjatost pak nelze řešit nezávisle na sobě, protože
na změna tvaru tělesa vlivem deformace vyvolá změnu napjatosti a obráceně.
12
Kde není deformace podstatná, uvolňujeme prvky ve stavu nedeformovaném
(PP I. řádu, případy prostého namáhání prutu – tah, ohyb, krut). Tam, kde deformace je podstatná, uvolňujeme prvky ve stavu deformovaném (PP II. řádu, vzpěr
prutů, ztráta stability stěn).
vzpěr na str. 92
Podle metody řešení dělíme pružnost a pevnost na
a) obecnou – z tělesa je nutno uvolňovat trojnásobně elementární prvek a určování
napjatosti a deformace je vzájemně závislé.
b) prostou – určení napjatosti a deformace jsou na sobě nezávislé procesy. Nutnou
podmínkou je
– uvolňování prvku v nedeformovaném stavu (PP I. řádu),
– formulace předpokladů, umožňujících použít jedno nebo dvojnásobně elementární prvek,
– využití Saint Venantova principu.
Saint Venantův
princip na str. 14
13
4. Napjatost v bodě tělesa
Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní
obecné napětí na hodnoty. Vektor obecného napětí f~, které působí v elementárním okolí bodu C na
str. 10
plošce dS s normálou ~en , charakterizuje napětí působící pouze v takto skloněném řezu
a neříká nic o tom, jaká napětí působí v jinak orientovaných rovinách vedených bodem C. Přitom pro vyloučení mezního stavu je nutno zajistit jistou rezervu vůči mezním
hodnotám napětí v kterékoli z těchto nekonečně mnoha rovin, v nichž působí různá
obecná napětí f~. Teprve souhrn všech těchto obecných napětí popisuje napěťový stav
v tomto bodě a zavádíme pro něj název napjatost v bodě tělesa.
Napjatost (napěťový stav) v bodě tělesa je množina obecných napětí ve všech řezech,
které lze tímto bodem vést.
Otázkou je, kolik elementárních plošek a jak orientovaných je nutno k úplnému určení
stavu napětí neboli napjatosti v bodu C. Dá se dokázat, že obecné napětí v libovolném řezu vedeném bodem C lze vypočítat ze známých hodnot obecných napětí ve třech
vzájemně kolmých řezech, vedených tímto bodem. Pro popis je účelné použít kartézský
souřadnicový systém, jehož osy leží v průsečnicích těchto rovin. Obecná napětí budeme označovat písmenem podle normály plochy, ve které působí, tedy např. v plošce
v rovině yz, kolmé k ose x, působí obecné napětí f~x . Každé obecné napětí, které svírá
s příslušnou plochou obecný úhel, lze rozložit do směrů os kartézského souřadnicového
systému:
f~x = σx~i + τxy~j + τxz~k,
f~y = τyx~i + σy~j + τyz ~k,
f~z = τzx~i + τzy~j + σz~k,
kde parametry σi (i = x, y, z) jsou normálová napětí, τij (i, j = x, y, z; i 6= j) smykové
napětí, první index i je směr normály roviny, ve které napětí působí a j udává směr
působení τij .
Poznámka
Tato tři obecná napětí lze sestavit vhodným způsobem do
čtvercové matice, která reprezentuje v uvedené kartézské
souřadnicové
napětí Tσ :
soustavě tenzor
σx τxy τxz
Tσ = τyx σy τyz
τzx τzy σz
Napjatost v bodě tělesa je jednoznačně určena tenzorem napětí Tσ .
V lineární pružnosti, vycházející mj. z předpokladu malých deformací, nejsou všechny
složky tenzoru Tσ nezávislé. Lze to doložit z momentové podmínky statické rovnováhy
elementárního prvku. Uvolníme-li uvnitř spojitého tělesa trojnásobně elementární prvek, v jeho rovinných stěnách (souřadnicové roviny yz, xz a xy) působí obecná napětí f~i .
V protilehlých stěnách působí obecná napětí f~i′ .
14
Poznámka ke znaménkové konvenci:
Z obrázku je patrné, jak jsou zavedeny kladné složky
tenzoru napětí – působí na kladných“ stěnách
”
(vnější normála je orientována souhlasně s některou ze souřadnicových os) ve smyslu kladném. Na
záporných“ stěnách kvádru (orientace vnější nor”
mály v záporném smyslu souřadnicové osy) působí
kladné složky v záporném smyslu os.
Z momentových podmínek k bodu C, který je v těžišti elementu, plyne
X
dy
dx
′
′
′
′
MCz = 0 : (τxy +τxy )dydz
− (τyx +τyx )dxdz
= 0 ⇒ (τxy +τxy
)−(τyx +τyx
) = 0.
2
2
Obecná napětí v přední a zadní stěně elementu (s normálou z) nejsou v obrázku zakreslena z důvodu přehlednosti. Výslednice objemových (např. tíhových) sil působících na
prvek prochází jeho těžištěm C, jejich moment k tomuto bodu je tedy nulový. Napětí
′
′
v protilehlých stěnách elementu jsou přibližně stejně velká (platí τxy → τxy
a τyx → τyx
),
~
proto τxy = τyx . Analogicky z momentových podmínek pro složky MC ve směru os x
a y plyne τyz = τzy a τxz = τzx .
Prvky tenzoru Tσ umístěné symetricky kolem hlavní diagonály (smyková napětí) jsou shodné, jinými slovy u smykových napětí nezáleží na pořadí indexů.
Obecně lze tyto relace zapsat rovnicí τij = τji ,
slovně ji vyjadřuje
věta o sdruženosti smykových napětí. Smyková napětí působící ve vzájemně kolmých elementárních řezech kolmo k jejich průsečnici jsou stejně veliká a orientovaná buď
k průsečnici nebo od ní.
sdruženost smyStav napětí je tedy charakterizován právě 6 nezávislými složkami symetrického ten- kových napětí
na str. 57
zoru napětí T .
σ
Napjatost v bodě tělesa je popsána tenzorem napětí v tomto bodě a může být
stanovena v závislosti na zatížení tělesa, jeho tvaru a materiálových vlastnostech
a poloze bodu v tělese.
Napjatost tělesa je množina napjatostí ve všech bodech tělesa. Je určena tenzorovým polem, tj. množinou tenzorů napětí pro všechny body tělesa. Závisí na zatížení
tělesa, jeho tvaru a materiálových vlastnostech.
Napjatost tělesa označujeme jako homogenní, jestliže napjatost ve všech bodech
tělesa je shodná, tj. tenzory napětí ve všech bodech tělesa jsou totožné.
4.1. Saint Venantův princip
Při řešení praktických problémů pružnosti obvykle neznáme rozložení vnějších sil působících na povrch tělesa a musíme je nahrazovat zjednodušeným modelem silového
působení (osamělá síla, silová dvojice, plošná síla konstantní velikosti atd.). Základní
otázkou použitelnosti výsledků v praxi je, jak se změní napjatost tělesa, když soustavu
vnějších sil nahradíme jinou staticky ekvivalentní soustavou.
15
ekvivalence
str. 122
na Podrobné rozbory ukazují, že napjatost tělesa
(tj. stav napětí v jednotlivých bodech tělesa) způsobená silovou soustavou Π působící na části povrchu ΓS o lineárním rozměru δ se liší podstatně
od napjatosti téhož tělesa zatíženého jinou, staticky
ekvivalentní silovou soustavou působící na ΓS , pouze
v takovém objemu materiálu v okolí plochy ΓS , jehož
rozměry se řádově shodují s rozměrem δ.
Znázorníme-li průběh jedné složky tenzoru napětí (např. σx ) podél přímky vedené
tělesem, a to pro původní rozložení sil (realita R) a pro náhradní, staticky ekvivalentní
(SE) rozložení (1 a 2), vidíme, že v dostatečné vzdálenosti od bodu A jsou napětí
prakticky stejná.
Uvedené skutečnosti formuluje pro PP zcela zásadní věta, označovaná jako Saint Venantův princip.
Saint Venantův princip. Nahradíme-li v určité oblasti tělesa jednu silovou soustavu
jinou, staticky ekvivalentní soustavou, pak napjatost tělesa je pro obě zatížení prakticky stejná s výjimkou blízkého okolí oblasti náhrady, jehož rozměry δ jsou srovnatelné
s rozměry této oblasti.
Význam Saint Venantova principu:
a) umožňuje správně používat výpočtové modely silového působení (objemových a plošných sil)
b) umožňuje správně zavádět výpočtové modely styku těles
c) lze usuzovat na nesprávnost
používání některých zjednodušení, která jsou běžná ve
statice, při řešení napjatosti
a deformace
Podle Saint Venantova principu je tedy v pružnosti a pevnosti možné nahrazovat silovou
soustavu jinou, staticky ekvivalentní silovou soustavou. Přípustnost tohoto nahrazení
je však závislá na mezních stavech, které rozhodují o provozní schopnosti skutečného
tělesa.
16
Jestliže provozní schopnost tělesa je určena mezními stavy
v podtělese ΩM , pak přípustné nahrazení je takové,
když ΩM neobsahuje žádný bod oblasti ΩS (oblast ovliněná
náhradou silového působení na ploše ΓS ). Jinak řečeno, oblast, ve které provádíme staticky ekvivalentní náhradu silového působení, není rozhodující pro vznik mezních stavů.
V opačném případě je nahrazení obecně nepřípustné.
Někdy je možné připustit SE náhradu i v případě, kdy se oblasti ΩS a ΩM překrývají.
Je to tehdy, když oblast nahrazení je relativně malá vůči řešenému tělesu a riziko
vzniku mezních stavů je při zatížení náhradní silovou soustavou poněkud vyšší
než ve skutečnosti (viz příklad výpočtového modelu na obrázku).
17
5. Deformace těles
deformace
str. 120
na S deformací jako složkou mechanického pohybu jste se setkali už ve statice. Běžně
je chápána jako změna rozměrů a tvaru tělesa. Lze ji popsat změnami vzdáleností
různých dvou bodů tělesa a změnami úhlů daných třemi body tělesa při dodržení jeho
spojitosti. Tyto změny jsou však pozorovatelné jen na povrchu tělesa, zatímco v praxi
se mohou vyskytnout i případy, u nichž dochází k deformacím jen uvnitř tělesa, aniž
by se podstatně měnily jeho rozměry a tvar.
Např. v případě lokálních objemových změn vlivem nerovnoměrnosti teploty nebo nerovnoměrných fázových přeměn
v materiálu (svařování, kalení a jiné technologické operace)
dochází k deformačním posuvům části vnitřních bodů tělesa. Jestliže okolní materiál je značně tuhý, mohou být
změny tvaru a rozměrů tělesa zanedbatelné, i když deformační posuvy některých vnitřních bodů tělesa v důsledku
těchto procesů jsou tak velké, že vedou ke vzniku mezních
stavů (např. vznik trhlin při kalení nebo svařování).
Deformaci tělesa je tedy třeba vymezit obecněji:
Deformace tělesa je změna tvaru a rozměrů tělesa a změna tvaru a rozměrů každého
jeho prvku vymezeného ve výchozím stavu.
Abychom mohli deformaci matematicky popsat, potřebujeme definovat polohu bodů
tělesa pomocí polohových vektorů jak ve výchozím (nedeformovaném), tak v zatíženém
(deformovaném) stavu.
K popisu můžeme použít dvě různé vztažné soustavy, v nichž definujeme souřadnicové
systémy, nejčastěji kartézské:
vztažný systém
na str. 3
obecné napětí na
str. 10
a) globální – počátek spojen se základním tělesem,
b) lokální – počátek spojen s libovolným vybraným bodem tělesa a osami vhodně orientovanými
vzhledem k řešenému problému. (Takovýto souřadnicový systém jsme např. použili při rozkladu
obecného napětí f~ v řezu na složku normálovou
a smykovou.)
Změna polohového vektoru kteréhokoli bodu tělesa
znamená posuv tohoto bodu; protože těleso jako celek nekoná pohyb vůči globálnímu souřadnicovému systému, v němž definujeme polohové vektory, je tento posuv dán deformací tělesa a jedná se tedy o deformační
posuv (~rd = ~rA′ − ~rA ).
Posuv (deformační posuv) bodu tělesa je dán změnou jeho polohového vektoru.
Je-li posuv dvou bodů tělesa různý, mění se vlivem deformace jejich vzdálenost; tuto
změnu délky je možné vypočítat odečtením vektorů jejich posuvů. Definujeme-li na
tělese jakýkoli úhel pomocí tří jeho bodů, vektorová algebra umožňuje ze změny polohových vektorů těchto tří bodů vypočítat změnu tohoto úhlu. Lze tedy říci, že z posuvů
bodů tělesa lze určit jakýkoli jeho deformační parametr.
Deformace tělesa je jednoznačně dána množinou posuvů všech jeho bodů.
18
Posuvy bodů tělesa jsou jeho základními deformačními charakteristikami, které
umožňují stanovit délkové a úhlové změny v tělese.
posuv
délkové změny
úhlové změny
změna polohy bodu tělesa
změna vzdálenosti dvou bodů změna úhlu daného třemi
body tělesa
Významnou vlastností deformace je, že ji lze omezeně pozorovat a měřit. Omezeně
proto, že jsme schopni měřit jen konečný a prakticky značně omezený počet deformačních charakteristik tělesa.
Pro posouzení deformačních mezních stavů tedy není
nutné popisovat deformaci tělesa úplně, ale stačí vybrat
pouze ty charakteristiky, které jsou důležité z funkčního
hlediska.
Například u rotujícího hřídele, na který je nasazeno kolo,
je důležité posoudit
– průhyb hřídele v místě rotoru,
– úhel prohnutí v místě ložisek,
– změnu průměru rotoru v důsledku odstředivých sil.
Deformace tělesa je obecně v každém jeho bodě různá, proto k popisu lokální deformace
zavádíme veličinu deformace v bodě tělesa.
Zavedení této veličiny můžeme ilustrovat pomocí experimentu, znázorněného na obrázku. Na povrchu tělesa je narýsována pravidelná pravoúhlá síť, která se při zatěžování
tělesa deformuje.
Při hrubé síti a nerovnoměrné deformaci tělesa dojde k tomu, že každý z původně
stejných čtverců sítě bude mít po deformaci jiný tvar. Budeme-li tuto síť zhušťovat,
dospějeme do stádia, kdy sousední čtverce zůstanou i po deformaci téměř geometricky
podobné. Deformace uvnitř vyznačeného čtverce pak již bude prakticky homogenní
→ stejná ve všech jeho bodech. Nerovnoměrnost pole deformací v tělese rozhoduje
o tom, při jaké jemnosti“ sítě k tomu dojde. Naprosto přesně to lze zajistit pouze
”
nekonečným zmenšením délky hrany čtverce, tj. limitním přechodem a → 0. Protože
v trojrozměrném prostoru představuje čtverec sítě elementární prvek ve tvaru krychle,
můžeme pak deformaci této krychle ztotožnit s deformací v libovolném jejím bodě.
19
Deformace elementární krychle je dána poměrnými změnami délek tří jejích hran a tří
úhlů mezi jejími stěnami, popsanými následujícími vztahy:
– délková přetvoření (poměrná změna délek):
′
′
′
εx = dx − dx , εy = dy − dy , εz = dz − dz
dx
dy
dz
(ε > 0 → prodloužení, ε < 0 → zkrácení),
– úhlová přetvoření – zkosy (změna pravých úhlů):
γxy = π2 − ϕxy , γxz = π2 − ϕxz , γyz = π2 − ϕyz .
Tyto veličiny lze podobně jako složky napětí uspořádat do
čtvercové matice popisující v dané souřadnicové soustavě
tenzor přetvoření Tε (někdy nepřesně nazývaný tenzor deformace).
γxy γxz
εx
2
2
Tε =
γyx
2
εy
γyz
2
γzx
2
γzy
2
εz
Tenzor přetvoření je tedy určen šesti souřadnicemi, a to třemi délkovými a třemi
úhlovými přetvořeními. Pak lze vyslovit následující definici:
Deformace v bodě tělesa je poměrná deformace elementárního prvku tělesa, který
tento bod tělesa obsahuje. Je popsána tenzorem přetvoření Tε .
otázka
Kontrolní
otázky
Termín deformace“ může tedy znamenat dvě různé fyzikální veličiny:
”
1. deformační posuvy [mm],
2. přetvoření – poměrná bezrozměrná veličina.
Mezi těmito významy je třeba přesně rozlišovat.
20
6. Zatížení tělesa
Zatížení tělesa je souhrn vnějších účinků působících na těleso a vnitřních procesů
deformace
na
v tělese, jejichž důsledkem je vznik deformace a napjatosti v tělese.
str. 18
Zatížení lze dělit na:
napjatost
na
str. 14
a) silové zatížení – deformace tělesa je vyvolána předepsaným vnějším silovým působením na těleso (síly osamělé [N], liniové [N/m], plošné [N/m2] a objemové [N/m3], zatížení silové na
str. 120
případně silové dvojice [Nm], jejichž hodnoty jsou předem známy);
b) deformační zatížení – deformace tělesa je primární (řízenou) veličinou (stano- Priklad 402
vení některého deformačního parametru tělesa, např. nasazení náboje na hřídel
s přesahem, utažení šroubu, prohnutí tyče o předepsanou hodnotu), vnější síly Příklad 405
vznikají jako důsledek známé deformace a jejich hodnoty nejsou předem známy; Příklad 418
c) objemové zatížení – deformace tělesa je vyvolána změnou objemu částí tělesa,
ke kterým může docházet vlivem změn teploty (teplotní zatížení) nebo vlivem Příklad 409
fázových přeměn ve struktuře materiálu.
Reálné zatížení tělesa je obvykle kombinace uvedených typů. Často dochází ke změně
teploty tělesa, jehož deformace jsou v prostoru omezeny - kombinace teplotního a deformačního zatížení atp.
Priklad 406
Za určitých okolností (nehomogenní fázové přeměny, lokální překročení meze kluzu) nemusí napjatost, resp. deformace vymizet ani po odlehčení tělesa a existuje v něm nadále
jako vlastní napjatost (zbytková, technologická, montážní). Je způsobena zatěžováním tělesa v minulosti, např. technologickými operacemi (kalením, litím, tvářením za
studena, svařováním atd.) nebo v průběhu provozu (při lokálním překročení mezního
stavu pružnosti v omezeném objemu materiálu). Určení vlastní napjatosti je velmi obtížné, neboť je stejně jako deformace závislá nejen na okamžitém zatížení tělesa, ale
i na historii zatěžování, což je sled všech zatěžovacích stavů tělesa od jeho vzniku
do současnosti.
Zatěžování tělesa je vždy proces probíhající v čase, jehož součástí mohou být následující zatěžovací stavy tělesa:
1. Nezatížený (výchozí) stav – je stav tělesa na počátku zatěžování, tedy bez
napětí.
2. Výrobní stav – stav, v němž mohou existovat zbytková napětí vyvolaná technologickými postupy při výrobě tělesa (kalení, svařování, tváření atd.).
3. Montážní stav – je stav, v němž mohou navíc existovat napětí vyvolaná montáží
soustavy (předpjaté šrouby, nalisování s přesahem).
4. Provozní stav – jeden z řady zatěžovacích stavů, kterým může být těleso
v průběhu technického života vystaveno při plnění požadovaných funkcí. Některé
z těchto stavů mohou být vyvolány předepsanými zkouškami zařízení (tlaková
zkouška potrubí, zátěžová zkouška mostu apod.)
5. Přechodový stav - stav, v němž těleso
– není schopno nadále plnit požadované funkce, ale je možné funkčnost tělesa
obnovit opravou nebo jiným zákrokem,
– těleso je nadále schopno plnit požadované funkce pouze se zhoršenými technickými parametry, neodpovídajícími původním technickým podmínkám (účinnost, ekonomie provozu, spotřeba paliva, bezpečnost provozu, přípustné zatížení, ergonomie – uživatelský komfort atd.)
21
– těleso je schopno nadále plnit pouze některé z požadovaných funkcí.
6. Mezní stav - těleso musí být pro nezpůsobilost k plnění požadovaných funkcí
vyřazeno z provozu.
Obvykle se při výpočtovém hodnocení nerozlišuje mezi přechodovými a mezními stavy;
někdy záleží na úrovni posuzování: např. mezní stav pístu nebo ojnice je přechodovým
stavem pro motor nebo celé vozidlo, protože funkčnost motoru lze obvykle snadno
obnovit výměnou porušené součásti. Nadále budeme všechny přechodové a mezní stavy
označovat jako mezní.
VVÚ na str. 41
tah na str. 53
ohyb na str. 78
krut na str. 71
Kontrolní
otázky
Poznámka:
Namáhání tělesa je název používaný pro odlišení charakteru pomocných veličin (normálová a posouvající síla, ohybový a kroutící moment), které vystupují u prutů ve
vztazích pro výpočet napětí a deformace. Rozlišujeme základní jednoduchá namáhání
(v závorce je uvedena nenulová složka výsledných vnitřních účinků (VVÚ) charakteristická pro daný typ namáhání):
–
–
–
–
tahem a tlakem (normálová síla),
smykem (posouvající síla),
ohybem (ohybový moment),
krutem (kroutící moment).
22
7. Základní formulace lineární PP
Podle tvaru závislosti mezi vnějšími silami a deformačně–napěťovými parametry tělesa
dělíme pružnost a pevnost na lineární a nelineární.
Lineární pružnost vyšetřuje napjatost a deformaci těles na základě předpokladu, že
všechny závislosti mezi parametry zatížení, napjatosti a deformace těles jsou lineární.
Porušení linearity u kterékoliv z těchto závislostí vede k úlohám označovaným jako úlohy
nelineární pružnosti.
Posouzení, kdy je pružnost lineární nebo nelineární, má zcela zásadní význam pro
řešení úloh PP, a tedy i pro posuzování konstrukcí. Úlohy lineární jsou podstatně
jednodušší z hlediska řešení, ale jejich praktická použitelnost je omezená.
Nutné podmínky pro lineárnost úlohy:
–
–
–
materiál těles je lineárně pružný,
malé deformační posuvy těles (v porovnání s jejich rozměry),
složky tenzoru přetvoření malé (≪ 1, obvykle nejvýše
řádu 10−3 ),
–
okrajové podmínky lineární
Příklad 623
.
V pružnosti a pevnosti I se budeme zabývat případy, kdy odchylky od linearity jsou
nepodstatné.
7.1. Hookův zákon
Zavedli jsme pojem pružné deformace“ tělesa jako deformaci, která je vratná. To
”
znamená, že deformace v daném okamžiku je závislá jen na parametrech zatěžování
v tomto okamžiku – nezávisí tedy na historii zatěžování. V důsledku toho je i napjatost
tělesa určena okamžitými parametry zatěžování.
Závislost mezi napětím σ a přetvořením ε má obecně tvar podle
obrázku, je nelineární. Tato nelinearita komplikuje významně
řešení úloh PP.
U nejběžnějšího strojírenského materiálu – oceli – je však
možné tuto závislost v celém pružném oboru s dostatečnou
přesností považovat za lineární. Dostáváme tak výpočtový model pružného materiálu – materiál lineárně pružný (hookovský), jehož vlastnosti popisuje Hookův zákon.
Hookův zákon je nejjednodušší formou konstitutivních (fyzikálních) relací. Tyto vztahy
obecně popisují závislosti mezi složkami tenzoru napětí Tσ a tenzoru přetvoření Tε ve
vyšetřovaném bodě tělesa. Jedná-li se o popis deformačně-napěťového chování lineárně pružného materiálu, pak je mezi složkami přetvoření a napětí lineární závislost.
V případě jednoosé napjatosti (realizuje se např. při tahové nebo tlakové zkoušce) je jedinou nenulovou složkou tenzoru napětí Tσ normálové napětí v podélném směru vzorku
(osa x) σx a závislost mezi tímto napětím a přetvořením v podélném směru je dána
23
rovnicí
σx = Eεx ,
kde E je konstanta úměrnosti nazývaná Youngův modul pružnosti nebo modul
pružnosti v tahu (v tlaku má u drtivé většiny materiálů stejnou hodnotu). Protože
při tahové nebo tlakové zkoušce dochází i ke změně příčných rozměrů vzorku (stav
deformace není jednoosý, nýbrž trojosý), jsou nenulová i ostatní délková přetvoření
a lze je určit ze vztahu
εy = εz = −µεx,
kde µ je tzv. součinitel příčné kontrakce neboli Poissonovo číslo. Protože u izotropního materiálu (jeho vlastnosti nejsou směrově závislé) nedochází při tahové zkoušce
ke zkosům (γij = 0 pro všechna i, j), jsou těmito vztahy definovány všechny složky
tenzoru přetvoření. K popisu lineárně elastického chování izotropního materiálu tedy
postačují uvedené 2 materiálové konstanty, které obě lze určit z jediné zkoušky (tahem). Pro neizotropní materiál jsou elastické vlastnosti směrově závislé a pro popis
konstitutivních vztahů nejobecnějšího anizotropního lineárně elastického materiálu je
zapotřebí 21 elastických konstant. Výše uvedené jednoduché vztahy však nestačí ani
pro popis lineárně elastického chování izotropního materiálu, protože jejich platnost je
omezena na případ jednoosé napjatosti. Pro víceosou napjatost jsou délková přetvoření
funkcí všech normálových napětí a obráceně. Tyto vztahy popisuje obecný Hookův zákon, z nějž lze odvodit i další zjednodušený tvar Hookova zákona platný pro smykovou
napjatost (v rovině):
τ = Gγ.
V něm konstanta úměrnosti G se nazývá modul pružnosti ve smyku. Běžně se
u izotropních materiálů neměří, protože z rovnic obecného Hookova zákona vyplývá
vztah pro jeho výpočet ve tvaru
G=
E
.
2(1 + µ)
7.1.1. Obecný Hookův zákon
Obecný Hookův zákon popisuje lineární závislost každé složky tenzoru napětí (přetvoření) na všech složkách tenzoru přetvoření (napětí).
U izotropního materiálu lze tuto závislost vyjádřit pomocí dvou elastických konstant E a µ. Lze jej zapsat maticově ve tvaru
σ =D·ε
nebo
ε = D−1 · σ,
kde σ je sloupcová matice tvořená šesti složkami Tσ , ε je taktéž sloupcová matice
tvořená šesti složkami Tε a D je čtvercová matice elastických modulů (D−1 matice
inverzní), z jejichž 36 prvků je díky symetrii pouze 21 nezávislých (pro anizotropní materiál). Počet vzájemně nezávislých složek je dán vnitřní symetrií materiálu. Nejvyšší
symetrii (tj. všechny mechanické vlastnosti nezávislé na směru v prostoru) má materiál označovaný jako izotropní. Pro něj lze všechny prvky matice elastických modulů
vyjádřit pomocí 2 nezávislých elastických konstant E a µ.
24
Pak lze maticovou rovnici rozepsat do šesti algebraických rovnic nazývaných zobecněný Hookův zákon [2]:
2(1 + µ)
τxy =
E
2(1 + µ)
=
τyz =
E
2(1 + µ)
=
τzx =
E
1 [σ − µ(σ + σ )]
εx = E
x
y
z
γxy =
1 [σ − µ(σ + σ )]
εy = E
y
x
z
γyz
εz = 1 [σz − µ(σx + σy )]
E
γzx
τxy
G
τyz
G
τzx
G
Explicitním vyjádřením složek napětí lze dostat inverzní tvar Hookova zákona:
σx =
σy =
σz =
τyz =
τxz =
τxy =
Eµ
E ε +
(ε + εy + εz ) = 2Gεx + λ (εx + εy + εz )
x
(1 + µ)
(1 + µ)(1 − 2µ) x
Eµ
E ε +
(ε + εy + εz ) = 2Gεy + λ (εx + εy + εz )
(1 + µ) y (1 + µ)(1 − 2µ) x
Eµ
E ε +
(ε + εy + εz ) = 2Gεz + λ (εx + εy + εz )
(1 + µ) z (1 + µ)(1 − 2µ) x
E
γ = Gγyz
2(1 + µ) yz
E
γ = Gγxz
2(1 + µ) xz
E
γ = Gγxy
2(1 + µ) xy
kde λ bývá nazýváno Lamého konstanta.
7.2. Práce síly při deformaci tělesa
Každá síla, jejíž působiště se posunuje, koná práci. Obecně můžeme
tuto práci vyjádřit vztahem
AF =
Z
F~ d~uA =
u
Z
F duF ,
uF
kde vektor d~uA představuje elementární posuv působiště síly a duF je průmět tohoto
vektoru do směru síly. Hodnotu integrálu (a tedy práci) lze vypočítat pouze za předpokladu, že známe závislost velikosti síly na poloze.
Předpokládejme, že na lineárně pružné těleso působí jediná osamělá síla F~ v bodě A.
Vlivem jejího působení se těleso deformuje, zatěžující vnější síla je v rovnováze
s vnitřním působením v tělese a musí se tedy také lineárně měnit se změnou polohy F (uF ) = c · uF v celém intervalu okamžitých hodnot uF ∈ h0; uFK i, roste tedy
z hodnoty 0 na konečnou hodnotu FK = c · uFK . Během tohoto děje pak tato proměnná
síla vykoná práci
uFK
AF =
Z
0
uFK
F duF =
Z
0
cu2FK
F2
1
cuF duF =
= K = FK uFK .
2
2c
2
25
Integrál si lze geometricky představit jako plochu pod křivkou
v grafu F = F (uF ) a při lineární závislosti síly a posuvu
odpovídá obsahu znázorněného trojúhelníka.
Budou-li na uvedené těleso působit i další síly, může se poloha síly F~ změnit i jejich
vlivem. Můžeme také určit práci, kterou síla F~ vykoná vlivem změn jiných sil (a sama
se přitom nemění). Tato práce konstantní síly při posunutí uF jejího působiště podél
nositelky z bodu 0 do uFK je
uFK
AF =
Z
FK duF = FK uFK .
0
Grafická interpretace tohoto integrálu je obdélník a výsledek skutečně odpovídá jeho
obsahu.
7.3. Obecné věty lineární pružnosti
V lineární pružnosti platí několik vět zásadní důležitosti, z nichž si uvedeme tyto:
7.3.1. Věta o superpozici
Příklad:
na prut působí 2 osamělé síly F~1 a F~2 . Prodloužení prutu je rovno součtu prodloužení způsobených jednotlivými silami (∆l = ∆l1 + ∆l2).
Pozor! Věta platí pouze pro lineární část diagramu (lineární pružnost), např. pro šedou litinu
superpozice neplatí, protože tahový diagram je od
počátku nelineární.
Napjatost a deformace tělesa zatíženého silovou soustavou je v lineární pružnosti rovna
součtu napjatostí a deformací způsobených jednotlivými silami této soustavy.
7.3.2. Věta o vzájemnosti prací (Bettiho věta)
Uvažujme
n o n nosník
o
sil F~1 ∪ F~2 .
zatížený soustavou
dvou
osamělých sil
danou
množinou
V průběhu zatěžování se nosník deformuje, působiště sil se posouvají. Označme posuv působiště síly F~i po její nositelce způsobený silou F~j symbolem uij . Analogický význam mají indexy
u práce.
Uvažujme 2 historie zatěžování:
1. Nejprve zatížíme silou F~1 a pak připojíme sílu F~2
26
n o
n
o
n
o
n
~0 → F~1 → F~1 ∪ F~2
o
.
n o
n
o
Při zatěžování ~0 → F~1 vykoná síla F~1 deformační práci A11
1
danou vztahem
A11 = F1u11.
2
n
o
n
o
n
o
Analogicky při zatěžování F~1 → F~1 ∪ F~2 vykoná síla F~2
1
práci
A22 = F2u22,
2
a současně, protože síla F~2 vyvolá posuvy všech bodů prutu
(s výjimkou nepohyblivě vázaných), vykoná síla F~1 práci
A12 =
u11R+u12
u11
F1du12 = F1u12 a celková práce je
1
1
A1 = A11 + A22 + A12 = F1 u11 + F2u22 + F1u12.
2
2
~
~
2. n
Uvažujme
o
n nyní
o opačný
n o postup.
n o Nejprve zatížíme silou F2 a pak připojíme sílu F1
~0 → F~2 → F~2 ∪ F~1 .
Obdobným způsobem dostaneme práci:
1
1
A2 = A22 + A11 + A21 = F2u22 + F1u11 + F2u21 .
2
2
Protože při zatěžování tělesa v pružném stavu nezávisí napjatost
ani deformace na historii zatěžování, nezávisí na historii zatěžování ani deformační práce (silová soustava je konzervativní,
tedy zachovávající energii). Proto musí platit
A1 = A2 .
Po dosazení dostaneme
1
1
1
1
F1u11 + F2u22 + F1 u12 = F2u22 + F1u11 + F2u21
2
2
2
2
a po úpravě
F1u12 = F2u21 .
Tato rovnost vyjadřuje nejjednodušší podobu Bettiho věty. Slovně ji lze vyjádřit takto:
Bettiho věta:
Při působení F~1 a F~2 na lineárně pružné těleso platí:
Práce síly F~1 na složkách deformace vyvolaných silou F~2 je rovna práci síly F~2 na složkách
deformace vyvolaných silou F~1.
Větu je samozřejmě možné zobecnit i na silové soustavy. Pro nás je však podstatnější její
zjednodušení zavedením jednotkových sil. Jsou-li obě síly jednotkové (F1 = F2 = 1), lze
je v rovnici vykrátit. Příslušné posuvy pak nazýváme příčinkové součinitele a platí
pro ně
η12 = η21.
V souladu se zavedeným značením posuvů pak např. součinitel η12 znamená posuv
působiště síly F~1 od jednotkové síly F~2 . Tyto příčinkové součinitele jsou již pro dané
těleso a jeho zvolené body charakteristickými konstantami. Lze z nich snadno určit
27
~
posuv působiště síly při
n zatížení
o tělesa silovou soustavou. Např. posuv působiště F1 při
~
~
zatížení soustavou sil F1; F2 je dán vztahem
u1 = F1η11 + F2η12 .
7.3.3. Deformační práce soustavy osamělých sil
Na lineárně pružné těleso působí soustava osamělých sil Π = {F~1, F~2}. Protože
deformační práce nezávisí na zatěžovací historii, zvolíme zatěžování tak, že nejprve necháme působit sílu F~1, pak přidáme sílu F~2, atd. Pak deformační práce:
{~0} → {F~1}
⇒ A1 = 12 F1u11.
{~0} → {F~1} → {F~1} ∪ {F~2} ⇒ A2 = A1 + 12 F2u22 + F1u12 =
= 12 F1(u11 + u12) + 12 F2u22 + 12 F1u12.
Využitím Bettiho věty dostaneme
F1u12 = F2u21
⇒
1
1
A2 = F1 (u11 + u12) + F2 (u21 + u22)
2
2
Protože platí ui = ui1 + ui2 , dostáváme pro práci celé soustavy
2
2
2
1 X
1 X
1X
A = F1
F i ui ,
u1i + F2
u2i + · · · =
2 i=1
2 i=1
2 i=1
kde ui je celkový posuv působiště síly F~i ve směru její nositelky vlivem všech působících
sil. Sumu lze samozřejmě zobecnit na libovolný počet sil.
Působí-li na lineárně pružné těleso soustava osamělých sil Π = {F~1, F~2 , · · · F~n }
a označíme-li posuvy jejich působišť A1, A2 , · · · An ve směru nositelek u1, u2 , · · · un , pak
platí
n
1
1
1
1X
F i ui .
A = F 1 u1 + F 2 u2 + · · · + F n un =
2
2
2
2 i=1
Deformační práce při působení silové dvojice
Na lineárně pružné těleso působí silová dvojice určená mo~ jehož velikost je M = 2rF . Posuvy působišť
mentem M,
sil silové dvojice můžeme vyjádřit ve tvaru u = r tg ϕ a pro
malý úhel (což je předpoklad lineární pružnosti a pevnosti)
.
( tg ϕ = ϕ) platí u = rϕ. Práce silové dvojice je:
1
1
1
1
1
1
A = F1u1 + F2u2 = F rϕ − F (−rϕ) = F 2rϕ = Mϕ
2
2
2
2
2
2
a) Natočení tělesa ϕ v bodě A je určeno změnami směrových úhlů přímky pevně spojené s tělesem v bodě A.
b) Deformační práce osamělé silové dvojice je: A = 12 Mϕ,
kde úhel ϕ udává natočení v rovině silové dvojice mezi výchozím a deformovaným
stavem.
28
7.3.4. Věta Castiglianova
Castiglianovu větu zde odvodíme zjednodušeně pro prutové těleso. Pro zájemce je k dispozici i navazující obecné odvození Castiglianovy věty. Mějme prut zatížený dvěma
silami podle kap. 7.3.2. Deformační práce A vykonaná při jeho zatěžování (pro prut
z elastického materiálu je rovna vratné energii napjatosti W ) je lineární funkcí zátěžných sil, která byla odvozena ve tvaru
1
1
A = W = F 1 u1 + F 2 u2 .
2
2
Oba posuvy působišť sil u1 a u2 jsou rovněž lineárními funkcemi obou zátěžných sil.
Tyto posuvy lze vyjádřit pomocí příčinkových součinitelů η ve tvaru
u1 = F1η11 + F2η12
u2 = F2η22 + F1 η21
Význam příčinkových součinitelů byl vysvětlen v kap. 7.3.2. Bettiho věta. Po dosazení
do uvedené rovnice pro výpočet deformační práce dostaneme pro energii napjatosti
vztah
1 2
F1 η11 + F1 F2η12 + F22η22 + F1F2 η21 ,
W =
2
který lze již snadno derivovat podle kterékoli síly (příčinkové součinitele ηij jsou pro
dané těleso a dané body konstanty). Např. derivací podle F1 dostaneme:
1
∂W
= (2F1 η11 + F2η12 + F2 η21) .
∂F1
2
∂F1 = 0 = ∂F2 . )
Přitom vycházíme ze vzájemné nezávislosti sil (tzn. ∂F
∂F1
2
Protože pro příčinkové součinitele platí nezávislost na pořadí indexů (η12 = η21 jako
důsledek Bettiho věty), lze vztah upravit do tvaru
1
∂W
= (2F1 η11 + 2F2 η12) = u1.
∂F1
2
Zobecněním pro J -tou sílu soustavy osamělých sil dostáváme 1. část Castiglianovy
věty:
∂W
uJ =
.
∂FJ
Působí-li na prut navíc silová dvojice MJ , vykoná při zatěžování tělesa práci
1
A = W = M J ϕJ ,
2
kde ϕJ je úhel natočení přímky spojené s tělesem v působišti momentuMJ . Pak za
podmínek vzájemné nezávislosti vnějších momentů a sil lze dojít stejným postupem
k analogickému vztahu pro 2. část Castiglianovy věty:
ϕJ =
∂W
.
∂MJ
Slovně lze pak obě části vyjádřit následovně:
29
Posuv působiště síly F~J po její nositelce je dán parciální derivací celkové energie napjatosti tělesa (soustavy) podle této síly.
Příklad 422
~ J v rovině jejího působení je dán parÚhel natočení v místě působení silové dvojice M
ciální derivací celkové energie napjatosti tělesa (soustavy) podle této silové dvojice.
Castiglianova věta je nejdůležitější větou lineární pružnosti z hlediska praktického použití, protože umožňuje počítat deformační charakteristiky jakéhokoli lineárně pružného
tělesa, pokud umíme matematicky formulovat vztah pro jeho energii napjatosti. Celou
soustavu těles musíme do energie napjatosti zahrnout tehdy, jestliže deformace okolních těles (resp. základního tělesa) nejsou zanedbatelné v porovnání s deformacemi
vyšetřovaného tělesa.
Poznámka:
Záporné znaménko posuvu (úhlu natočení) znamená, že tento posuv (toto natočení)
nastává proti smyslu působení příslušné síly (silové dvojice). Castiglianova věta je proto
nezávislá na znaménkových konvencích, protože kladná práce znamená vždy posuv ve
smyslu působící síly.
Obecné odvození Castiglianovy věty
Uvažujme izotropní těleso, na které působí obecná silová soustava Π
(jednu sílu z této silové soustavy s působištěm v bodě J označíme F~J ).
Tato silová soustava vykonala deformační práci A. Je-li těleso v lineárně pružném stavu, nezávisí deformační práce na historii zatěžon
P
vání: A =
Ai , kde Ai je práce vykonaná i-tým prvkem silové soui=1
stavy. Vykonaná práce se projeví zvýšením energie napjatosti (viz 7.3.3)
n
n
P
P
1F u .
∆W =
Ai =
i i
i=1
i=1 2
Zderivujeme energii napjatosti (parciálně) podle velikosti síly F~J :
∂W
∂A1 ∂A2
∂AJ
∂An
=
+
+ ··· +
+ ··· +
.
∂FJ
∂FJ
∂FJ
∂FJ
∂FJ
Každý člen tohoto součtu se dá s ohledem na jeho definici zapsat
∂Ai
1 ∂ui
1 ∂Fi
= Fi
+
ui
∂FJ
2 ∂FJ 2 ∂FJ
a protože z definice práce plyne Fi = ∂W a dále ∂Fi je jen 1 nebo 0, tak
∂ui
∂FJ
n
n
n
X
∂W
∂Ai
1X
∂ui
1
1X
∂W ∂ui
1
=
=
Fi
+ uJ =
+ uJ .
∂FJ
2 i=1 ∂FJ 2
2 i=1 ∂ui ∂FJ 2
i=1 ∂FJ
Suma v posledním výrazu představuje zápis parciální derivace složené funkce, dá se
tedy rovnice napsat ve tvaru
∂W
1 ∂W
1
=
+ uJ
∂FJ
2 ∂FJ
2
=⇒
∂W
= uJ .
∂FJ
~ dostaneme druhou
Když budeme místo osamělé síly F~ uvažovat silovou dvojici M,
část Castiglianovy věty. Jiným postupem jsme dospěli k téže matematické formulaci
Castiglianovy věty, kterou lze rozšířeně vyslovit takto:
30
Castiglianova věta:
Působí-li na lineárně pružné těleso (soustavu) silová soustava, pak posuv uJ působiště
síly F~J po její nositelce je dán parciální derivací celkové energie napjatosti tělesa (sou∂W .
stavy) podle této síly uJ = ∂F
Příklad 422
J
~ J v rovině jejího půÚhel natočení ϕJ přímky spojené s působištěm silové dvojice M
sobení je dán parciální derivací celkové energie napjatosti tělesa (soustavy) podle této
∂W .
dvojice ϕJ = ∂M
J
31
8. Základní vlastnosti pružně plastického materiálu
Jestliže při zatěžování z výchozího do konečného stavu a odlehčení do
výchozího stavu vznikají trvalé (plastické) deformace (∆lt) říkáme, že
těleso je v pružně plastickém stavu. Silově deformační závislost je
odlišná při zatěžování a odlehčování.
Fyzikální vztahy pružně plastického materiálu jsou obecně značně složité, proto i řešení
napjatosti a deformace těles v pružně plastickém stavu je oproti stavu elastickému
obtížnější. Touto problematikou se zabývá teorie plasticity.
Pružně plastické chování je rozhodující pro posuzování mezních stavů pevnosti a únosnosti ocelových konstrukcí. Proto při pevnostních výpočtech se jím musíme zabývat.
V základní pružnosti a pevnosti se ale budeme zabývat pouze nejjednoduššími případy.
Obecné vlastnosti materiálu a těles v pružně plastickém stavu můžeme vyjádřit těmito větami:
– Závislost mezi zatížením, napjatostí a deformací je vždy nelineární ⇒ neplatí
superpozice.
– Napjatost a deformace v daném okamžiku je závislá na celé historii pružně plastického zatěžování.
– Pružně plastický stav materiálu nastává až po překročení mezního stavu pružnosti.
– Nejjednodušší výpočtové modely pružně plastického materiálu nahrazují křivku σ − ε nad mezí kluzu přímkou. Podle
jejího sklonu rozlišujeme modely chování materiálu:
a) materiál ideálně pružně plastický – nulový sklon,
b) materiál s lineárním zpevněním – nenulový sklon.
– Odlehčíme-li úplně těleso ze zatíženého stavu, který vyvolal
vznik plastických deformací, vznikne v tělese reziduální (zbytková) napjatost (za podmínky, že v plastickém stavu byla napjatost v tělese nehomogenní).
32
9. Tahová a tlaková zkouška
Má-li být PP prakticky použitelná, pak podstatné vlastnosti materiálu reálných těles
musí být vyjádřeny konstitutivními vztahy a materiálovými charakteristikami, které
jsou určovány experimentálně. S materiálovými zkouškami jste se seznámili v předmětu
Nauka o materiálu. Mezi těmito zkouškami je základní tzv. tahová a tlaková zkouška.
Při této zkoušce je vzorek zatěžován monotónně
rostoucím prodloužením ∆l, přičemž se zjišťují závislosti zatěžující síly F a změny příčných rozměrů ∆d v měrné části vzorku. Ta je vymezena
tak, aby v ní vznikala homogenní jednoosá
napjatost (ve všech bodech shodná napjatost,
tj. totožné všechny složky napětí).
9.1. Tahová zkouška materiálu v houževnatém stavu
Výsledkem tahových zkoušek je tahová závislost
smluvních napětí a přetvoření σ(ε), která pro typicky
houževnatý materiál má tvar podle obrázku. Můžeme
zde rozlišit tyto významné body:
0 – nezatížený stav
D – dolní mez kluzu
L – hranice lineární závislosti P – maximální zatížení
E – hranice pružného chování F – počátek lomu
H – horní mez kluzu
T – porušení celistvosti
Dále lze rozlišit tři typické oblasti: I. oblast pružných deformací, II. oblast rovnoměrných pružně plastických deformací a III. oblast nerovnoměrných pružně plastických
deformací.
9.1.1. Oblast pružných deformací (I)
– Závislost σ(ε) je na strojírenské rozlišovací úrovni shodná při zatěžování a odlehčování.
– Lineární část závislosti σ(ε) můžeme vyjádřit Hookovým zákonem pro jedoosou
napjatost ve tvaru σ = Eε s konstantou úměrnosti E (modul pružnosti v tahu).
Pro oceli je E ∈ (1, 9; 2, 4) · 105 MPa.
– Pro délková přetvoření vzájemně kolmých příčných rozměrů platí
εy = εz = −µεx .
V oblasti pružných deformací je Poissonovo číslo µ konstantní a jeho hodnota pro
všechny typy ocelí je přibližně µ = 0, 3. Při tahovém zatížení tyče s původními
rozměry l0 , a0, b0 se její délka zvětší na l a příčné rozměry zmenší na a a b.
Délková přetvoření jsou
εx = ε =
l − l0
a − a0
b − b0
, εy =
, εz =
.
l0
a0
b0
33
homogenní
napjatost
na
str. 14
jednoosá napjatost na str. 99
– Oblast pružných deformací je ohraničena mezí kluzu σK . Je to smluvní hodnota
ležící pod body L, E, H, D na tahové křivce materiálu.
9.1.2. Oblast rovnoměrných pružně plastických deformací (II)
Pro většinu materiálů platí
– deformace měrné části vzorku zůstává homogenní, tj. válcová tyčka zůstává válcovou;
– změny rozměrů vzorku mohou být značné, takže skutečné napětí neodpovídá hodnotám určeným z výchozího nedeformovaného průřezu;
– závislost σ(ε) při zatěžování je nelineární;
– závislost σ(ε) při odlehčování je na strojírenské rozlišovací
úrovni lineární;
– tato oblast končí v bodě P, v němž zatěžující síla dosahuje
své maximální hodnoty – odpovídá smluvní mezi pevnosti σP t . Tato charakteristika v rozporu se svým názvem
nevystihuje dosažení meze pevnosti materiálu, kdy nastává
jeho porušení, ale vystihuje pouze přechod od rovnoměrných deformací k deformacím nerovnoměrným.
My se v pružnosti a pevnosti budeme pružně plastickým chováním zabývat jen omezeně
– svou náročností to přesahuje rámec základního studia. Rovněž z hlediska konstruování
je to oblast obvykle nepoužitelná – velké plastické deformace nelze u většiny strojních
dílů připustit.
9.1.3. Oblast nerovnoměrných pružně plastických deformací (III)
napjatost
trojosá na str. 99 V této oblasti má závislost σ(ε) klesající charakter, což znamená, že
prodlužování tyče nastává při klesajícím smluvním napětí. Je to důsledek toho, že deformace se lokalizují do malé oblasti, kde vzniká místní
zúžení, tzv. krček. V oblasti krčku je nerovnoměrná trojosá napjatost.
Globální charakteristikou nerovnoměrné deformace je kontrakce
z=
porušení
str. 7
na
S0 − S
.
S0
Oblast končí přetržením tyče, tedy tvárným lomem, který je konečným
stadiem mezního stavu porušení za podmínek monotonně rostoucí
deformace.
9.2. Tlaková zkouška materiálu v houževnatém stavu
Při tlakové zkoušce je realizace experimentu problematická, protože
– je třeba vyloučit změnu přímosti tyče a zamezit prohýbání střednice (musí se
používat krátké tyče, l0 < 1, 5d),
34
– chceme dosáhnout rovnoměrné deformace a tím i rovnoměrné napjatosti, tedy je nutno zajistit rovnoměrné zatížení čel prutu tlakem v celém průběhu zatěžování (problém: dochází ke zkracování délky a zvětšování průměru
prutu, kterému brání tření mezi čelem vzorku a čelistí zařízení, což má za následek vznik smykových napětí a změnu
jednoosé napjatosti na obecnou. Zkušební vzorek dostává
soudečkovitý tvar).
Tlaková zkouška poskytuje tyto důležité závěry:
napjatost
str. 99
na
1. mez kluzu je u většiny materiálů stejná při tahu i při tlaku
.
(σKt = σKd = σK ),
2. elastické konstanty E a µ jsou přibližně stejné jako u tahu,
3. na rozdíl od tahu nedochází při tlaku k lokalizaci plastických
deformací,
4. síla potřebná k rozvíjení plastických deformací trvale
vzrůstá,
5. u vysoce tvárných materiálů nevzniká při tlaku vůbec
tvárný lom.
9.3. Tahová a tlaková zkouška materiálu v křehkém stavu
Za určitých podmínek (teplota, rychlost zatěžování, napjatost, . . . )
nedochází v makroobjemu materiálu ke vzniku plastických deformací.
Pak u jakéhokoliv materiálu může vzniknout křehká trhlina. Za podmínek tahové zkoušky (nízká rychlost zatěžování, jednoosá napjatost)
vzniká křehký lom především u materiálů
– s charakteristickou strukturou (šedá litina, keramické materiály),
– u ocelí vykazujících tranzitní chování (v závislosti na působení jistých faktorů, především teploty, se porušují tvárným nebo křehkým
lomem).
Rychlost šíření křehké trhliny je vysoká (u oceli cca 1000 ms−1 ), takže
křehký lom nastává po vzniku trhliny prakticky okamžitě. K šíření
křehké trhliny postačuje pružná energie napjatosti naakumulovaná
v tělese v okamžiku vzniku křehké trhliny. Jejímu šíření proto již nelze
zabránit zásahem do zatěžování tělesa.
Na závislosti σ(ε) jsou významné body odpovídající mezi křehké
pevnosti v tahu σRt a mezi křehké pevnosti v tlaku σRd .
Realizace tlakové zkoušky materiálu v křehkém stavu má stejné
problémy jako u materiálu v tvárném stavu. Z jejího rozboru vyplývá:
1. mez křehké pevnosti v tlaku je vždy větší než mez křehké pevnosti v tahu (σRd > σRt ),
2. křehký lom vzniká rovnoběžně s osou vzorku. Není-li odstraněno tření mezi čelem vzorku a čelistí zařízení, vznikají lomy
pod určitým úhlem (cca 45o ).
35
tahová zkouška
na str. 33
10. Prut v pružnosti a pevnosti
Základním úkolem PP je řešit problémy spojené s napjatostí, deformací a porušováním
součástí technických objektů, což jsou většinou tvarově složitá tělesa. Určení napjatosti
a deformace těles složitějších geometrických tvarů bylo umožněno až pomocí počítačů.
Předtím bylo možné jen řešení určitých geometricky jednodušších těles, a to ještě při
předpoklady na použití řady omezujících předpokladů.
str. 11
My se teď budeme zabývat nejjednodušším modelovým tělesem, a to prutem. V běžném jazyce chápeme prut jako těleso dlouhé a tenké“, ale v PP si musíme prut vyme”
zit přesněji. Toto vymezení na jedné straně zavádí další omezující podmínky, na druhé
straně umožňuje zahrnout i tělesa, která nejsou dlouhá a tenká“.
”
Prut v PP je nejjednodušším teoretickým modelem reálného tělesa, které splňuje jisté
geometrické, vazbové, zatěžovací, deformační a napjatostní předpoklady (označujeme je
jako prutové předpoklady).
10.1. Prutové předpoklady
a) předpoklady geometrické
– Prut je určen střednicí γ, a v každém bodě střednice
příčným průřezem ψ.
– Střednice γ je spojitá a hladká křivka konečné délky.
– Příčný průřez je jednoduše nebo vícenásobně souvislá oblast, ohraničená obrysovou křivkou, matematicky ji popisujeme charakteristikami příčného průřezu.
charakteristiky
na str. 38
Příkladem nesouvislého příčného průřezu je řez A-A v místě
drážky v prutu obdélníkového průřezu (porušení prutových
předpokladů).
– Délka střednice je vždy podstatně větší než největší rozměr
příčného průřezu.
Pro popis prutu se používá obvykle pravotočivý kartézský souřadnicový systém, jehož
osa x má směr tečny ke střednici a osy y, z jsou vhodně zvoleny v příčném průřezu.
b) předpoklady vazbové a zatěžovací
– Vazby omezují jen posuvy a úhly natočení střednice.
36
– Zatížení je soustředěno na střednici, tj. silovým působením
na prut jsou osamělé nebo liniové síly a silové dvojice s působištěm na střednici (není–li splněno, nutná staticky ekvivalentní (SE) náhrada reálného zatížení zatížením na střednici;
přitom je třeba mít na paměti omezení plynoucí ze Saint Venantova principu).
silové působení
na str. 120
SE na str. 122
c) předpoklady deformační
– Střednice zůstává v procesu deformace
spojitá a hladká.
– Průřezy v procesu deformace zůstávají rovinné a kolmé k deformované střednici,
pouze se vzájemně
– oddalují (tah),
tah na str. 53
přibližují (tlak),
– natáčejí kolem osy ležící v příčném průřezu a deformují (ohyb),
ohyb na str. 78
– natáčejí kolem osy kolmé k příčnému průřezu a nedeformují (krut),
krut na str. 71
– posouvají kolmo ke střednici (smyk).
d) předpoklady napjatostní
prutová napjatost na str. 99
Napjatost v bodě prutu je určena normálovým a smykovým napětím
v příčném řezu vedeném tímto bodem; ostatní složky tenzoru napětí
jsou nulové. Tuto napjatost nazýváme prutová napjatost.
σx τxy 0
σ τ 0
Tσ = τyx 0 0 = τ 0 0
0
0 0
0 0 0
σx 0 τxz
σ 0 τ
nebo Tσ = 0 0 0 = 0 0 0
τzx 0 0
τ 0 0
Pro řešení problémů deformace a napjatosti prutu budeme používat dva typy prvků:
– prvek konečný Ω0 , uvolněný z prutu jedním příčným řezem ω1 ,
– prvek jednonásobně elementární Ω1 ,
uvolněný z prutu dvěma limitně blízkými
příčnými řezy ω1 , ω2 (je základním prvkem prutů).
37
Tento základní prvek bude často vhodné chápat jako soustavu tvořenou trojnásobně
elementárními prvky, určenými prvkem dψ příčného průřezu ψ a prvkem dγ střednice
prutu γ.
10.2. Geometrické charakteristiky příčného průřezu
Jsou to veličiny, které charakterizují příčný průřez, a jsou používány ve vztazích pro
výpočet napětí a deformace pro jednotlivé způsoby namáhání.
10.2.1. Plocha příčného průřezu
S=
Z
dS =
ψ
ZZ
h
dydz
ψ
m2
i
10.2.2. Lineární (statické) momenty
Uy =
Z
zdS,
Uz =
ψ
těžiště
str. 125
Z
h
m3
ydS
ψ
i
na S lineárními momenty jste se setkali už ve statice při určování polohy těžiště:
R
~rT = ΩR
~rdFG
Ω
pro ρ = konst., t = konst. ~rT =
Příklad 101
R
dFG
~rdS
Ψ
S
⇒
yT =
R
ydS
Ψ
S
Uz
=
,
S
zT =
R
zdS
Ψ
S
=
Poznámka:
Lineární moment k ose procházející těžištěm průřezu (centrální osa) je roven nule.
10.2.3. Kvadratické momenty
název
osové
definiční vztah
Jy =
R
z 2 dS,
rozměr příklad použití
[m4]
napětí a deformace v ohybu (určované
ψ
ohyb na str. 79
krut na str. 73
R
Jz = y 2 dS,
v hlavním souřadnicovém systému)
ψ
deviační
polární
R
yzdS,
[m4]
JP = r2 dS,
[m4]
Jyz =
ψ
R
ψ
určení polohy hlavního souřadnicového
systému
napětí a deformace v krutu středově symetrických průřezů
38
Uy
S
10.2.4. Základní vlastnosti kvadratických momentů průřezu
1. Aditivnost: kvadratické momenty celého průřezu ψ k daným osám jsou rovny
součtu kvadratických momentů částí průřezu ψi k těmže osám.
2. Hodnoty osových a polárních kvadratických momentů jsou kladné. Hodnota deviačního momentu může být jakékoliv reálné číslo (obojí plyne z vlastností integrálů).
3. Osové momenty dvou symetrických průřezů k ose symetrie jsou stejné. Totéž platí
pro jakoukoli osu kolmou k ose symetrie obou průřezů. Deviační momenty k těmto
Příklad 102
osám jsou rovněž stejné, ale opačných znamének.
Ψ1 = Ψ2 , Jz(1) =
Důkaz:
Z
y 2 dS =
Ψ1
Jy(1) =
Z
z 2dS =
Ψ1
(1)
Jyz
=
Z
Ψ1
Z
(−y)2dS = Jz(2)
Ψ2
Z
z 2 dS = Jy(2),
Ψ2
yzdS = −
Z
Ψ2
(2)
yzdS = −Jyz
⇒
(1)+(2)
(1)
(2)
Jyz
= Jyz
+ Jyz
= 0.
Odtud plyne: deviační moment symetrického průřezu k pravoúhlému souřadnicovému systému, kde alespoň jedna z os je osou symetrie, je roven nule.
4. Polární kvadratický moment je dán součtem osových kvadratických momentů
k osám pravoúhlého souřadnicového systému s počátkem v pólu.
Důkaz:
r2 = y 2 +z 2 ⇒ JP =
R
ψ
R
R
R
r2 dS = (y 2 +z 2)dS = y 2 dS+ z 2dS = Jz +Jy
ψ
ψ
ψ
10.2.5. Kvadratické momenty základních tvarů průřezů
a) Obdélník
R
Jyz
h/2
R
b/2
3
3
R
R
z 2 bdz = bh
, Jz = y 2 dS =
y 2hdy = hb
,
12
12
ψ
ψ
−h/2
−b/2
R
= yzdS = 0
Jy = z 2 dS =
ψ
39
b) Trojúhelník
y(z)
h−z
b
b
b = h → y(z) = b − h z, dS = (b − h z)dz
3
R
Rh
hb3 , J = h2b2
Jy = z 2 dS = z 2 (b − hb z)dz = bh
,
J
=
z
12
12 yz
24
0
ψ
Poznámka: pro praktické použití je třeba tyto momenty transformovat
posunutím a natočením, protože nejsou vztaženy k hlavnímu centrálnímu souřadnicovému systému (viz dále).
c) Kruh
Jy = Jz ,
R
Jy + Jz = JP ⇒ Jy = 12 JP , dS = 2πρ · dρ, JP = ρ2 dS,
ψ
4
4
4
RR
JP = ρ2 2πρ · dρ = πR
, Jy = Jz = J2P = πR
= πD
, Jyz = 0
2
4
64
0
10.2.6. Kvadratické momenty průřezu při transformaci souřadnic
ohyb na str. 79
Transformačních vztahů s výhodou využíváme při určování kvadratických momentů
průřezu. Určíme kvadratické momenty k osám, ke kterým je výpočet nejsnadnější (nebo
je známe), a pak je transformujeme k hlavním centrálním osám. Tyto tzv. hlavní centrální osové kvadratické momenty se využívají např. pro výpočet napětí a deformace
při namáhání ohybem.
a) Transformace posunutím
Příklad 103
Příklad 04
Steinerovy věty
Pomocí známých kvadratických momentů k centrálním osám yT
a zT (osy procházející těžištěm) určujeme tyto momenty k posunutým osám y a z (nebo naopak):
Jy = JyT + b2 S,
Jz = JzT + a2S,
Jyz = JyT zT + abS.
Protože členy a2 S i b2 S jsou vždycky kladné, je kvadratický moment ke kterékoliv
posunuté ose větší než moment k ose rovnoběžné centrální (procházející těžištěm).
Příklad 110
b) Transformace natočením
Pro transformaci natočením lze odvodit následující vztahy:
Jy ′
Jz ′
Jy ′ z ′
JP ′
= Jy cos2 α − Jyz sin 2α + Jz sin2 α
= Jz cos2 α + Jyz sin 2α + Jy sin2 α
J −J
= y 2 z sin 2α + Jyz cos 2α
= Jy ′ + Jz ′ = JP
10.2.7. Hlavní kvadratické momenty
V množině pootočených souřadnicových systémů y’, z’ existuje souřadnicový systém yh , zh , ke kterému je deviační moment roven nule (Jyh zh = 0). Nazývá se hlavní
souřadnicový systém a jeho osy jsou osy hlavní. Kvadratické momenty k tomuto
souřadnicovému systému se nazývají hlavní kvadratické momenty Jyh , Jzh . Jak
plyne z Mohrova zobrazení (viz 10.2.8), jeden z těchto hlavních kvadratických momentů je maximální (značíme J1 ) a druhý minimální (J2 ) mezi kvadratickými momenty
ke všem různě natočeným souřadnicovým systémům. Poloha hlavního souřadnicového
40
systému je dána úhlem mezi natočenými a původními osami, který se určuje z podmínky nulového deviačního momentu:
Jyh zh
Jy − Jz
=
sin 2αh + Jyz cos 2αh = 0
2
⇒
!
1
−2Jyz
αh = arctg
.
2
Jy − Jz
Hlavní souřadnicový systém s počátkem v těžišti se nazývá hlavní centrální souřadnicový systém. Protože osa symetrie průřezu vždy prochází jeho těžištěm a deviační
moment k ní je nulový, je tato osa vždy hlavní centrální osou, stejně jako osa k ní
kolmá jdoucí těžištěm.
Příklad 105
Příklad 107
Příklad 108
Příklad 109
10.2.8. Mohrova kružnice kvadratických momentů
Mohrovou kružnicí lze geometricky znázornit kvadratické momenty k souřadnicovým systémům různě
natočeným kolem bodu průřezu (obvykle kolem jeho
těžiště).
Na vodorovnou osu vynášíme osové kvadratické momenty, na osu svislou momenty deviační. Souřadnici Jy
přísluší deviační moment Jyz , souřadnici Jz pak přísluší deviační moment Jyz stejně velký, ale s opačným
znaménkem. (Tato konvence je dána odvozením Mohrovy kružnice.)
Příklad 106
Úhel 2αh mezi průvodičem bodu odpovídajícího osovému kvadratickému momentu Jy a vodorovnou osou
je dvojnásobkem úhlu mezi osou y a příslušnou hlavní
centrální osou příčného průřezu.
10.3. Výsledné vnitřní účinky prutů (VVÚ)
Řešíme úlohu pružnosti pro prutové těleso, na něž působí silová soustava Π. Viditelným úloha pružnosti
projevem odezvy jsou posuvy jednotlivých bodů tělesa, matematicky popsané vektoro- na str. 1
vým polem, tj. množinou vektorů posuvů ~uA = fu (Π). Vnitřním projevem odezvy jsou
stavy deformace a napjatosti tělesa v každém jeho bodě, popsané dvojicí vzájemně
závislých tenzorů přetvoření Tε a napětí Tσ .
Tσ na str. 14
Tε na str. 18
Při řešení složek napětí vycházíme z podmínek statické rovnováhy prvku tělesa.
rovnováha
na
41
str. 123
konstitutivní
Prut rozdělíme příčným řezem ω na dva konečné prvky Ω01
a Ω02. Statickou rovnováhu prvku Ω01 zajišťují vnitřní síly, mající obecně charakter sil spojitě rozložených v průřezu ω; pro
vyjádření těchto sil jsme zavedli veličinu obecné napětí f~ω . (Analogicky platí statická rovnováha pro prvek Ω02; jsou-li splněny
podmínky pro prvek Ω01 , budou automaticky splněny i pro prvek Ω02.)
Protože však použitelných podmínek statické rovnováhy je nejvýše šest, nestačí k určení
napětí, které může být v každém bodě řezu různé co do velikosti i směru; úloha určení
napětí v řezu je mnohonásobně staticky neurčitá. Aby úloha byla řešitelná, nahradíme
obecná napětí v řezu staticky ekvivalentně (SE) výslednicí silovou F~V a momento~ V v těžišti příčného průřezu (těžiště budeme nadále značit R kvůli vyloučení
vou M
záměny s označením tenzorů a posouvajících sil).
ekvivalence
str. 121
~ V jsou vektory dané každý
na Výslednice F~V i M
třemi složkami. Těchto celkem šest složek
nazýváme výsledné vnitřní účinky (VVÚ)
a určujeme je z rovnic statické rovnováhy (SR) uvolněného prvku Ω01 nebo Ω02 ,
vyjadřujících rovnováhu sil vnějších Π1 (působících nan prvek o
Ω01 resp. Ω02) a vnitř~
~
ních ΠV = FV , MV .
Znalost určování VVÚ je nutným předpokladem zvládnutí problému pružnosti prutů.
VVÚ jsou pomocné veličiny, popisující namáhání prutu a umožňující nalézt předem
nebezpečná místa prutu (tj. místa s největším namáháním).
Při definici složek VVÚ postupujeme následovně:
~ V rozložíme do směrů
Výslednici silovou F~V a momentovou M
lokálních souřadnicových os:
F~V = F~V x + F~V y + F~V z = N~i + Ty~j + Tz~k
~V = M
~Vx + M
~Vy + M
~ V z = Mk~i + Moy~j + Moz ~k
M
Jejich souřadnice jsou výsledné vnitřní účinky v bodě R střednice (VVÚ).
VVÚ = {N, Ty , Tz , Mk , Moy , Moz }
podmínky SR na VVÚ v bodě střednice se určují z podmínek statické rovnováhy uvolněného prvku.
str. 123
Lokální souřadnicový systém má počátek v těžišti R průřezu, ve kterém určujeme
osy na str. 36
složky VVÚ. Osa xL je u přímého prutu totožná se střednicí (v případě prutu zakřiveného je tečnou k zakřivené střednici), osy yL a zL leží v příčném průřezu a dohromady
tvoří kartézský souřadnicový systém.
Složky VVÚ mají zavedeny specifická označení a názvy:
N
tah na str. 53
krut na str. 71
ohyb na str. 78
Ty , Tz
Mk
Moy , Moz
/
\
- posouvající síly
- kroutící moment
- ohybové momenty - normálová síla
namáhání
namáhání
namáhání
namáhání
namáhání
42
tahem - směr vnější normály
tlakem - směr vnitřní normály
prutu smykem (střihem)
prutu krutem
prutu ohybem
Výsledné vnitřní účinky (VVÚ) jsou složky silové a momentové výslednice vnitřních
sil v těžišti příčného průřezu, které spolu se soustavou vnějších silových účinků tvořítěžiště
str. 125
rovnovážnou silovou soustavu působící na prvek prutu.
na
~ V ) jsou funkce popisující rozložení jednotlivých složek VVÚ poPrůběhy VVÚ (F~V , M
dél střednice prutu; tyto funkce jsou určeny tvarem střednice a silovým působením. silové působení
Střednice se při zatížení deformuje, proto se mohou v průběhu zatěžování měnit i F~V na str. 21
~ V v každém bodě střednice. VVÚ bychom proto měli vyjadřovat obecně vzhledem
aM
~V
k deformované střednici → pružnost a pevnost II. řádu. Když jsou změny F~V a M
~V
v důsledku deformace střednice nepodstatné, můžeme tyto změny zanedbat a F~V a M
určíme vzhledem k nedeformované střednici, tj. k výchozímu tvaru (PP I. řádu).
V tomto případě musíme určit deformaci a zkontrolovat, jestli deformace střednice podstatně VVÚ nezmění. Jestliže je podstatně změní, je výpočet chybný a správně by měl
být proveden znovu s uvažováním deformace střednice (PP II. řádu). My se však, až
na výjimky (vzpěrná stabilita prutů), budeme zabývat pružností I. řádu (deformace
prutu neovlivňuje podstatně jeho napjatost) a uvolňovat prvek v nedeformovaném
stavu.
V pružnosti a pevnosti prutů dále rozlišujeme podle počtu nenulových složek VVÚ:
– jednoduché namáhání prutu – jestliže v každém bodě střednice působí pouze
~ T~ , M
~ o, M
~ k . Označíme ho jako tah (N > 0), tlak (N < 0),
jedna ze složek N,
ohyb (Mo 6= 0), krut (Mk 6= 0), smyk (T 6= 0);
– kombinované namáhání prutu – jestliže alespoň v jednom bodě střednice prutu
~ T~ , M
~ o, M
~ k nenulová;
je více než jedna ze složek N,
nebo podle způsobu vyjádření VVÚ
a) VVÚ v bodě střednice: určitá hodnota, je potřebná pro určení lokálních charakteristik (napětí),
b) VVÚ prutu:
funkční závislost po délce střednice, potřebná pro určení nebezpečných průřezů a globálních charakteristik (deformační posuvy).
Znaménková konvence: O znaménkách N, Ty , Tz , Mk , Moy , Moz zavedeme tuto
úmluvu (existují i jiné úmluvy, v literatuře musí být použitá konvence uvedena):
Veličiny N, Ty , Tz , Mk , Moy , Moz považujeme za kladné, když mají smysl kladných (záporných) os lokálního souřadnicového systému pro uvolněný prvek obsahující počáteční L (koncový P) bod
střednice.
Poznámka:
Rozdílný smysl kladných složek VVÚ na levém (obsahujícím bod L) a pravém (obsahujícím bod P) prvku prutu je zaveden z důvodu respektování zákona akce a reakce
mezi oběma prvky prutu. Při dodržení této konvence dostaneme znaménkově shodné
výsledky, ať si pro řešení VVÚ vybereme kterýkoliv z těchto prvků.
10.4. Určování VVÚ
Úkolem je – vyjádřit VVÚ pro obecný bod střednice,
43
– znázornit průběh složek VVÚ podél střednice a určit místa jejich extrémů,
– určit extrémní hodnoty jednotlivých složek,
– vymezit na střednici oblasti stejného typu namáhání množinou nenulových složek VVÚ.
10.4.1. Přístupy k řešení průběhů VVÚ
Pro určování průběhů VVÚ se používají 2 základní přístupy:
a) Integrální přístup – založen na sestavení a řešení podmínek SR konečného prvku
prutu.
b) Diferenciální přístup – založen na sestavení a řešení podmínek SR elementárního prvku prutu.
Uvažujme přímý volný prut, jehož střednice je určena v globálním souřadnicovém systému bodem počátečním L (levý) a koncovým P (pravý). Prut je zatížen zadanou
obecnou silovou soustavou Π:
– osamělé síly F~i [N] v bodech Ai střednice, i =
1 ÷ n,
~ j [Nm] v bodech Bj
– osamělé silové dvojice M
střednice, j = 1 ÷ m,
– liniové síly dané měrným liniovým zatížením
~q(l) [Nm−1] podél střednice nebo její části γq ,
jejíž body označíme C.
Příklad 201
Příklad 202
Příčný průřez prutu nemusí být pro určování VVÚ zadán!
a) Integrální přístup
vychází z definice složek VVÚ, které určujeme z rovnic SR konečného prvku následovně:
1. Bodem R vedeme řez ω, rozdělí prut na dva
prvky: ΩL (obsahuje bod L) a ΩP (obsahuje
bod P).
2. VVÚ určujeme z podmínek rovnováhy jednoho
z těchto prvků. Je libovolné, který prvek pro řešení vybereme. Volíme prvek, pro který je řešení
jednodušší.
rovnováha
str. 123
konvence
str. 41
na
na
3. Na vybraný prvek (označíme ΩR ) s délkou střednice lR působí vnější silová soustava ΠR . Do řezu zavedeme složky VVÚ
~ V ) v kladném smyslu podle
(tj. složky F~V , M
znaménkové konvence. Prut je ve statické rovnováze, proto i prvek ΩR musí splňovat podmínky statické rovnováhy:
– silová podmínka:
P
lR
– momentová podmínka:
lRR
F~i + ~qi (l)dl + F~V = ~0
0
44
lR
~ i × F~i ) + P(M
~ j ) + R (RC
~ × ~q)dl + M
~ V = ~0
(RA
P
lR
lR
0
Z uvedených vektorových rovnic je patrné (jsou zde sumy a integrály), že
VVÚ v bodě R prutu, zatíženého vnější silovou soustavou, jsou součtem VVÚ od jednotlivých vnějších silových účinků.
4. Definujeme-li polohu bodu R střednice v globálním souřadnicovém systému (xR pro kartézský, ϕR pro polární),
můžeme určit kteroukoliv souřadnici VVÚ v závislosti
na poloze bodu R na střednici prutu, tj. určit průběh
VVÚ.
lokální s.s. na
str. 41
Důsledky znaménkové konvence:
~ směřuje ven
– kladná normálová síla N
z řezu,
– kladná posouvající síla T~ má snahu
otáčet prutem kolem bodu L i P ve
směru pohybu hodinových ručiček,
~ o defor– kladný ohybový moment M
muje střednici do konvexního tvaru
(červená křivka na obrázku - střed
křivosti nahoře)
Pravidla pro znaménka T a Mo lze jednoznačně použít jen u rovinné úlohy a vodorovného přímého prutu.
5. Kde je třeba vést řezy, abychom získali průběh VVÚ?
K určení VVÚ musí být prut popsán střednicí, která je spojitou a hladkou křivkou prutové předpoa soustavou zatěžujících prvků působících na střednici. Průběh VVÚ lze vyjádřit klady na str. 36
funkcí s konečným počtem bodů nespojitosti podél střednice. Tyto body představují hranice intervalů a v každém intervalu musí být zvolen jeden řez. VVÚ mají
tedy charakter funkcí, které na hranicích intervalů mohou být nespojité nebo mít
nespojitou derivaci.
6. Vyšetříme průběhy funkcí popisujících závislosti jednotlivých složek VVÚ na poloze řezu (znáte z matematiky) a určíme polohu extrémů (kromě hranic intervalů
mohou být v místech nulové derivace - viz matematika) analyticky nebo graficky.
V těchto tzv. nebezpečných bodech stanovíme funkční hodnoty jednotlivých slo- nebezpečný bod
žek VVÚ.
na str. 64
b) Diferenciální přístup
Vychází z diferenciálních závislostí mezi zatížením prutu a složkami VVÚ. Tyto závislosti (tzv. Schwedlerovy věty) je možné odvodit pro prut s obecnou střednicí, obecně
zatížený. Zde odvodíme diferenciální vztahy pouze pro přímý prut zatížený v rovině
obecným nekonstantním spojitým zatížením ~q(x).
45
Z prutu vyřízneme dvěma blízkými řezy jednonásobně elementární prvek Ω1 o délce
dx. Spojité zatížení ~q(x) rozložíme do normálového a tečného směru příčného průřezu
(~qT (x), ~qN (x)):
qN (x) = q(x) cos α,
qT (x) = q(x) sin α.
Zavedeme složky VVÚ, které se mezi oběma řezy budou vzájemně lišit o elementární
přírůstky dN, dT, dMo . Sestavíme použitelné podmínky statické rovnováhy, přičemž
vzhledem k elementárnosti prvku můžeme na něm spojité zatížení ~q považovat za konstantní (co do velikosti i směru):
X
Fx = 0 :
X
Fz = 0 :
N(x) + dN(x) − N(x) + qN (x)dx = 0
T (x) + dT (x) − T (x) + qT (x)dx = 0
dx
=0
2
Zanedbáme-li v poslední rovnici diferenciál 2. řádu oproti ostatním členům (diferenciály
1. řádu), dostaneme vztahy, označované jako Schwedlerova věta:
X
MR2 = 0 :
Mo (x) + dMo (x) − Mo (x) − T (x)dx + qT (x)dx
dN(x)
= −qN (x),
dx
dT (x)
= −qT (x),
dx
dMo (x)
= T (x).
dx
Podívejme se na tyto vztahy z hlediska významu derivace:
– Velikost spojitého zatížení qT nám určuje směrnici tečny k funkční závislosti T (x)
ve vyšetřovaném bodě střednice.
– Velikost posouvající síly T (x) v daném bodě střednice je směrnice tečny k průběhu
ohybových momentů.
Známe-li tedy průběh spojitého zatížení, je tím dán jednoznačně charakter průběhu
VVÚ. Pro určení konkrétních hodnot lze použít následující pomocná pravidla.
10.4.2. Pomocná pravidla pro vyšetřování průběhu VVÚ u přímých prutů
1. Skok v průběhu N(x) nebo T (x) (tj. směrnice tečny → ∞)
může být jen tam, kde působí vnější osamělá síla odpovídajícího směru (~q → ∞).
T > 0, jestliže vlevo od řezu působí příčná síla směrem
vzhůru.
2. V místě, kde je skok v průběhu T (x) (různá zleva a zprava),
musí být zlom v průběhu Mo (x) (různé směrnice).
Schwedlerova věta:
!
dMo (x)
= T (x) .
dx
46
3. Skok v průběhu Mo (x) může být jen tehdy, když v tomto
místě působí vnější silová dvojice.
Mo > 0, je-li střed křivosti ohybové čáry nahoře.
4. Je-li prut zatížen jen osamělými silami a dvojicemi (ne
spojitým zatížením), jsou průběhy N(x) a T (x) konstantní
a Mo (x) je tvořen pouze lomenými přímkami, nikoliv křivkami (plyne opět ze Schwedlerovy věty).
5. Kde průběh T (x) prochází nulou, má Mo (x) extrém.
dMo (x)
= T (x) = 0
dx
!
extrém
→
6. V průřezu prutu, kde je posouvající síla kladná (záporná),
je průběh Mo (x) rostoucí (klesající)
dMo (x)
(opět vyplývá ze Schwedlerovy věty: dx
= T (x)).
7. Podle zavedených konvencí je pro konvexní ohybovou čáru
Mo > 0. Přechod mezi konvexní a konkávní částí ohybové čáry je jejím inflexním bodem, ve kterém proto platí
Mo = 0.
8. Na konci prutu musí všechny složky VVÚ dosáhnout nulové
hodnoty, pokud zde nepůsobí odpovídající složka vnějšího
zatížení (ta by vyvolala skok VVÚ podle bodu 1 nebo 3).
9. Pro kreslení průběhu VVÚ je výhodné využít symetrie a antisymetrie prutů.
Je-li prut z hlediska geometrie symetrický a z hlediska vnějších silových účinků
(zatížení a sil ve vazbách)
symetrický, pak v rovině symetrie je
– nulová posouvající síla,
– extrémní ohybový moment,
– nulový kroutící moment,
antisymetrický, v rovině antisymetrie je
– nulová normálová síla,
– extrémní posouvající síla,
– nulový ohybový moment.
10.4.3. Otevřené vázané pruty
Vazbové deformační podmínky prutu
Vazbu kinematickou dvojicí popisuje množina kinematických vazbových para- vazby na str. 126
47
metrů (posuvy a natočení): v prostoru je to množina D3 = {u, v, w, ϕx, ϕy , ϕz }, v rovině D2 = {u, w, ϕ}. Je-li vazbou některý kinematický vazbový parametr z množiny Di
omezen, je odpovídající silový vazbový parametr (složka stykové výslednice) z množiny
S = {Fx , Fy , Fz , Mx , Moy , Moz } nenulový. Připomeňme zde základní typy rovinných vazeb:
Tyto vazby označujeme jako tuhé – omezený kinematický vazbový parametr je nulový.
Příklad 407
Lineárně pružné vazby jsou charakterizovány lineární závislostí mezi odpovídajícími složkami silových a kinematických vazbových parametrů (např. u = konst. Fx ).
Více se blíží realitě, používají se tam, kde deformace základního tělesa (rámu) nejsou
zanedbatelné oproti deformacím řešeného prutu. Problém je obvykle v praxi v určení
tuhosti (poddajnosti) těchto vazeb, kterou je často snazší stanovit experimentálně.
Jako vazbovou deformační podmínku označujeme rovnici, určující velikost
deformačního parametru omezeného vazbou tělesa. Tyto rovnice budou dále využívány
při řešení staticky neurčitých prutů.
Příklady vazbových deformačních podmínek tuhé a pružné vazby
Prut vázaný v n bodech střednice
Uvažujme prut v podmínkách prostého namáhání, který je vázán k základnímu tělesu
(rámu) v n bodech střednice. Pro řešení silových účinků ve vazbách prut uvolníme tak,
že odstraníme vazby a nahradíme je stykovými silami a silovými dvojicemi. Ve statice
statický rozbor jste se zabývali statickými rozbory, zavedli jste si µ jako počet neznámých nezávislých
na str. 128
silových parametrů (složky neznámých silových účinků) a ν jako počet použitelných
podmínek statické rovnováhy (závislý na typu silové soustavy). Na základě porovnání
těchto hodnot se rozhodovalo o statické určitosti (řešitelnosti) úlohy. V pružnosti a pev48
nosti jsou na rozdíl od dynamiky neznámými parametry pouze vazbové silové účinky,
proto lze hovořit o statické určitosti (resp. neurčitosti) uložení.
Posouzení statické určitosti může vést k následujícím závěrům:
a)
ν=µ
– uložení je staticky určité,
– neznámé nezávislé parametry stykových výslednic určíme z použitelných podmínek statické rovnováhy.
Prut je uložen nepohyblivě z hlediska pohybu jako celku, ale s možností
volné deformace (žádný deformační parametr není omezen).
b)
µ<ν
Prut není uložen nepohyblivě z hlediska pohybu jako celku. Tyto případy řeší dynamika, pak teprve případně pružnost a pevnost.
Dynamika není pro řešení nutná v případě, že pohyb tělesa je sice
možný, ale při daném zatížení nenastane. Úloha je staticky určitá
(µ = ν), i když nepohyblivost tělesa není uložením zajištěna.
c)
µ>ν
1. uložení je staticky neurčité,
stupeň statické neurčitosti s = µ − ν,
2. neznámých nezávislých parametrů stykových výslednic je víc
než použitelných podmínek statické rovnováhy,
3. pro určení neznámých nezávislých parametrů stykových výslednic je třeba kromě ν použitelných podmínek statické rovnováhy formulovat s vazbových deformačních podmínek.
Prut je uložen nepohyblivě z hlediska pohybu jako celku, navíc s omezenou deformací.
Při řešení využijeme částečného uvolnění.
Otevřené pruty vázané staticky určitě – postup řešení
Prut úplně uvolníme – tzn. nahradíme všechny stykové vazby stykovými výslednicemi, které určíme z podmínek statické rovnováhy a řešíme jako prut volný.
V některých případech (pruty s volným koncem) není pro stanovení VVÚ úplné uvolnění nezbytné.
49
deformační charakteristiky na
str. 18
Otevřené pruty vázané staticky neurčitě – postup řešení
1. prut uvolníme úplně – nahradíme všechny stykové vazby stykovými výslednicemi (reakcemi) a sestavíme použitelné podmínky statické rovnováhy.
Např.:
P
P
P
Fx = 0 :
Fz = 0 :
MA =
0:
2. prut uvolníme částečně – tj. na úroveň staticky určitého uložení
(uložení, při němž je v prostoru právě definována poloha prutu, ale není omezena jeho deformace) a sestavíme vazbové deformační podmínky, což jsou podmínky, které musí splňovat
uvolněné vazby.
Tvar deformační podmínky jednoznačně souvisí se způsobem částečného uvolnění.
Částečné uvolnění je uvolnění na úroveň staticky určitého uložení a zavedení deformačních podmínek tak, aby byla zachována deformace shodná s původním staticky
neurčitým uložením. Jeho cílem je formulace deformační podmínky.
Deformační podmínka je vazbová podmínka v místě uvolněné vazby při částečném
uvolnění. Je to právě ta chybějící“ rovnice, kterou potřebujeme k řešení neznámých
”
silových vazbových parametrů.
Deformační podmínky mohou být
Příklad 414
1. homogenní (s nulou na pravé straně rovnice) – u tuhých vazeb,
Příklad 418
Příklad 417
Příklad 419
2. nehomogenní – u poddajných vazeb, pruty s výrobní nepřesností, změnou teploty,
Příklad 437
3. podmíněné – u podmíněně funkčních vazeb.
50
Záporné znaménko plyne z použití Castiglianovy věty, u níž znamená posuv proti směru Castiglianova
věta na str. 26
působení síly F~B .
10.4.4. Uzavřené pruty - rámy
Určení VVÚ je u uzavřených prutů úloha vždy vnitřně staticky neurčitá. Uzavřený
prut totiž řezem nerozdělíme na prvky (části), ale pouze z něj vytvoříme prut otevřený.
Nemáme tedy žádné použitelné podmínky statické rovnováhy pro určení VVÚ. Podle
charakteru uložení k základnímu tělesu může být úloha také vně staticky neurčitá. Při
řešení je třeba převést uzavřený prut vhodně volenými řezy na prut otevřený a formulovat deformační podmínky. Detailně se řešením uzavřených prutů zabývat nebudeme.
10.4.5. Algoritmus určování VVÚ
1. Klasifikace prutu
– otevřený přímý prut vázaný staticky určitě - uvolnění a určení stykových sil
(pokud jsou zapotřebí);
– otevřený přímý prut vázaný staticky neurčitě - řešení lze provést pouze kvalitativně (pro kvantitativní řešení je zapotřebí částečně uvolnit a podmínky
statické rovnováhy doplnit o potřebné vazbové deformační podmínky);
– otevřený prut zakřivený - řešení podobné jako u prutu přímého, ale v tomto
případě i při nulovém spojitém zatížení nebudou silové složky VVÚ konstantní;
– prut uzavřený - vždy z hlediska určování průběhu VVÚ staticky neurčitý
(vnitřně), navíc může být vně staticky určitý anebo neurčitý. Vyjádření prů51
Příklad 203
integrální přístup na str. 43
diferenciální přístup na str. 43
běhu VVÚ je vždy relativně složitá úloha, která vyžaduje doplnit použitelné
podmínky statické rovnováhy o potřebné deformační podmínky.
2. Uvolnění prutu, sestavení podmínek statické rovnováhy a určení stykových sil
(je-li úloha staticky určitá a nejedná se o prut vetknutý).
3. Rozdělení prutu na úseky, a to ve všech bodech, kde
– působí osamělé vnější zatěžovací účinky (včetně stykových sil, resp. momentů);
– se mění charakter spojitého zatížení;
– se mění směr (zlom) nebo křivost střednice.
4. Rozhodnutí o dalším postupu (nemusí být pro všechny úseky stejný)
– integrální přístup (sestavování rovnic statické rovnováhy prvku) volím tehdy,
je-li úloha relativně obtížná, ale staticky určitá;
– diferenciální přístup (využití Schwedlerových vět) volím u relativně snadné
úlohy nebo vždy u úlohy staticky neurčité (kvalitativní řešení);
B) integrální přístup - v každém
úseku prutu provedeme kroky:
5. Uvolníme prvek prutu řezem vedeným v obecném bodě střednice řešeného úseku.
A) diferenciální přístup
pravidla
str. 43
na
5. Z 1. Schwedlerovy věty a zadaného průběhu spojitého zatížení určíme s využitím dalších pravidel
(10.4.2 Pomocná pravidla pro vyšetřování průběhu VVÚ) průběh silových složek VVÚ, resp. kroutícího
momentu.
6. Z průběhu posouvajících sil určíme
s využitím 2. Schwedlerovy věty
průběh ohybových momentů.
7. Z průběhu VVÚ odhadneme nebezpečné průřezy (místa lokálních extrémů) a v nich určíme číselné hodnoty složek VVÚ (není-li úloha staticky neurčitá).
6. Z podmínek statické rovnováhy
prvku určíme všechny složky VVÚ
(jako funkce souřadnice místa řezu).
7. Vyšetříme funkční závislosti průběhu VVÚ z hlediska lokálních
extrémů a určíme polohu těchto
extrémů.
8. Nakreslíme průběh funkčních závislostí VVÚ, určíme nebezpečné
příčné průřezy a vypočítáme číselné
hodnoty VVÚ v těchto průřezech.
Příklad 238
Poznámka: U prutů neprizmatických (s proměnným příčným průřezem) mohou existovat další nebezpečná místa daná lokálním zeslabením prutu. Tím se budeme zabývat
až při řešení napjatosti a deformace pro konkrétní typy namáhání.
52
11. Prostý tah a tlak
11.1. Definice
Prostý tah(tlak) je namáhání přímého prizmatického prutu, jestliže
– jsou splněny prutové předpoklady,
– příčné průřezy se vzájemně oddalují (přibližují) a následně izotropně deformují
prostá pružnost
(tj. mění velikost, ale nemění tvar),
na str. 12
– jedinou nenulovou složkou VVÚ je normálová síla N,
prutové předpo– deformace jsou z hlediska statické rovnováhy prvku nepodstatné.
klady na str. 36
Na základě tohoto vymezení odvodíme vztahy pro napětí a deformace.
Poznámka: jako prizmatický označujeme prut, jehož příčný průřez je v každém bodě
střednice stejný a hlavní centrální osy mají stejný směr (nešroubovitý).
11.2. Geometrické vztahy
Jsou to vztahy mezi posuvy a přetvořeními.
prvek na str. 10
Délková a úhlová přetvoření vyjádříme v závislosti na typu změny vzájemné polohy příčných
průřezů při zatěžování. Při tahovém (tlakovém)
zatížení prutu se průřezy ψ1, ψ2 jednonásobně elementárního prvku Ω1 , vzdálené o dx, oddálí (přiblíží) o deformační posuv du, který je stejný pro
všechny body ψ. Pravé úhly α, β se nezmění.
Těmto deformacím odpovídají následující složky tenzoru přetvoření.
(Poznámka: Neurčujeme všechny složky Tε , ale pouze ty, které mají některý index x.
Tak je podle zavedené konvence označena normála příčného průřezu, takže εx , γxy a γxz
definují jeho polohu a pomocí Hookova zákona z nich určíme odpovídající složky napětí.
Ostatní složky Tσ jsou podle napjatostních prutových předpokladů nulové. Podobně
tomu bude i u ostatních typů namáhání prutů.)
εx = du
dx
γxy = γxz = 0
(řezy zůstanou kolmé ke střednici)
Protože posuv du je stejný pro všechny body ψ (du(y, z) = konst.),
du
= konst.
dx
Přetvoření jsou tedy konstantní v celém příčném průřezu.
εx(y, z) =
Totéž platí i pro délková přetvoření v příčných směrech εy a εz , která jsou rovněž nenulová, opačného znaménka než εx (εy = εz = −µεx ).
εx 0 0
V prutu vzniká trojosý stav deformace. Tenzor přetvoření Tε = 0 εy 0 . tenzor přetvo0 0 εz
ření na str. 18
53
Hookův zákon 11.3. Rozložení napětí v příčném průřezu
na str. 23
Pro hookovský materiál (homogenní, lineárně pružný) platí lineární závislost
σx (y, z) = Eεx(y, z).
Protože εx (y, z) = konst., je i σx (y, z) = konst. = σ (v ψ rozloženo rovnoměrně).
prutové předpo- σy = σz = 0 - vyplývá z prutových předpokladů napjatostních (v ψ je prutová napjaklady na str. 36 tost).
G na str. 23
Pro smykové napětí platí vztah τij =
konstanta závislá na E a µ).
E
γ = Gγij , (G je pro izotropní materiál
2(1 + µ) ij
Protože γxy = γxz = 0, je i τxy = τxz = 0. Z prutových předpokladů plyne τyz = 0.
Tσ na str. 14
V prutu vzniká jednoosá napjatost. Tenzor napětí
σx 0 0
Tσ = 0 0 0 .
0 0 0
11.4. Závislost mezi VVÚ a napětím
Při známém rozložení napětí po průřezu již
vnitřní síly nepředstavují nekonečný počet neznámých parametrů (pro σ = konst. dokonce
pouze jediný) a je možné určit závislost normálového napětí σ na VVÚ. Použijeme k tomu podmínky statické ekvivalence mezi soustavou elementárních sil dN~i = σx dS ~i v příčném průřezu
a jejich silovou výslednicí N~i působící v těžišti
příčného průřezu.
statické
podmínky
str. 123
Sestavíme použitelné podmínky stana tické ekvivalence (3D soustava rovnoběžných sil ⇒ ν = 3):
X
ψ
Fx :
ZZ
σx dS = N,
ψ
σx = konst.
⇒
ZZ
ψ
σxdS = σx
ZZ
ψ
dS = N
⇒
σ=N
S
Ve výsledném vztahu už obvykle index x u napětí vynecháváme, protože ostatní složky
statická ekviva- napětí jsou nulové. Podmínka statické ekvivalence, z níž jsme vztah odvodili, však
lence na str. 122 platí pouze tehdy, jsou-li splněny všechny použitelné podmínky statické ekvivalence.
Pro použitelnost vztahu je tedy nutné zkontrolovat splnění zbývajících dvou podmínek
statické ekvivalence.
54
X
ψ
My :
ZZ
zσxdS = Moy ,
X
ψ
ψ
Mz : −
ZZ
statické
momenty na str. 38
yσdS = Moz .
ψ
Z definice prostého tahu plyne Moy = Moz = 0. Pak lze obě
podmínky upravit do tvaru
ZZ
ψ
z σdS = σ
ZZ
ZZ
z dS = σUy = 0,
ψ
yσdS = σ
ψ
ZZ
ydS = σUz = 0.
ψ
Podmínky SE jsou splněny, protože osy y a z procházejí těžištěm (Uy = 0, Uz = 0).
11.5. Extrémní napětí
Pro posuzování mezních stavů je důležité znát místa a extrémní hodnoty napětí v příč- mezní stavy na
ném průřezu. Jak jsme odvodili, u prostého tahu (tlaku) je napětí po průřezu rozloženo str. 5
rovnoměrně, tedy všechny body průřezu jsou stejně nebezpečné a extrémní napětí je
proto přímo dáno odvozeným vztahem
σex =
N
.
S
11.6. Energie napjatosti
V lineární pružnosti se celá deformační práce projeví zvýšením pružné energie napjatosti A = ∆W (práce vynaložená na trvalou deformaci AQ = 0).
deformační
Na trojnásobně elementární prvek Ω3 působí vnitřní elementární
~
práce na str. 26
síla σdS i. Změnu délky dx tohoto prvku označíme du. Deformační
práce vnitřní elementární síly (uvažujeme lineárně pružné těleso)
AσdS = 21 (σdS)du. Po dosazení za du = εdx a ε = σ/E dostaneme
vztah pro energii napjatosti uvažovaného elementárního prvku ve
tvaru
1
1 σ2
WΩ3 = A(σdS) = (σdS)εdx =
dSdx.
2
2E
Vztažením energie napjatosti na jednotku objemu dostáváme měrnou energii napjatosti
(nazývanou také hustota energie napjatosti)
Λ=
WΩ3
WΩ3
=
VΩ3
dSdx
⇒
2
Λ = 12 σε = 12 σE
Tyto vztahy platí obecně pro jednoosou napjatost určenou napětím σ nezávisle na typu
namáhání prutu.
Pro prostý tah platí σ = N
S a energie napjatosti jednonásobně elementárního prvku
Ω1 pak je
WΩ1 =
ZZ
ψ
1 σ2
dxdS =
2E
ZZ
ψ
N2
N 2 dx
dxdS
=
2ES 2
2ES 2
55
ZZ
ψ
dS =
N2
dx.
2ES
V prutu o délce l se pak akumuluje energie napjatosti
Wl =
Zl
WΩ1 =
0
Zl
0
N2
dx .
2ES
11.7. Vyjádření deformační charakteristiky střednice
Základní deformační charakteristikou u prostého tahu je posuv bodu střednice ve směru
střednice. Délkové přetvoření střednice εx = du/dx. Protože jsou splněny prutové předprutové předpo- poklady, zůstává střednice spojitá
spojitou funkcí. Pro hookovský
a posuv u(x) je
klady na str. 36 materiál ε = σx a prostý tah σ (x ) = N(xR) je posuv bodu střednice daného
x
x R
E
S(xR)
hookovský masouřadnicí xR
teriál na str. 23
ZxR
ZxR
N(x)
σx (x) na str. 54
u(xR) = εx dx =
dx,
ES(x)
xm
Příklad 432
Příklad 433
xm
kde xm je souřadnice bodu střednice, ve kterém je nulový posuv (obvykle vazba k základnímu tělesu).
Modul pružnosti E se také teoreticky může měnit po délce střednice (v příčném průřezu
předpoklady na však musí být konstantní, aby nedošlo k porušení předpokladů prostého tahu), ale
str. 53
v praxi se může vyskytnout jedině skoková změna (různé materiály po délce prutu).
Je-li v určitém úseku střednice N(x) = konst., E(x) = konst. a S(x) = konst.
a umístíme-li bod střednice s nulovým posuvem do počátku souřadnicového systému
(xm = 0), pak
u(xR ) =
NxR
,
ES
kde ES se označuje jako tuhost příčného průřezu v tahu.
11.8. Deformace příčného průřezu
Kromě podélných posuvů příčných průřezů při tahovém (tlakovém) namáhání prutu
nastane i změna jejich příčných rozměrů.
Poissonův součinitel udává poměr velikostí příčného přetvoření εy nebo εz k podélnému přetvoření εx, tedy
εy = εz = −µεx
Protože přetvoření v obou příčných směrech jsou stejná
a konstantní po průřezu, tvar příčného průřezu se nezmění. Z definice přetvoření konstantních po průřezu plynou vztahy pro změnu rozměrů obdélníkového průřezu
∆a a ∆b:
a − a0 = ∆a = εy a0 = −µεxa0 ,
b − b0 = ∆b = εz b0 = −µεx b0.
56
11.9. Rozbor napjatosti prostého tahu
Doposud jsme vyšetřovali napětí v příčném průřezu (s plochou S), tj. v řezu kolmém na
střednici, tedy napětí v jediném řezu vedeném zvoleným bodem střednice. Napjatost napjatost
jsme však definovali jako množinu napětí ve všech řezech, které lze vést daným bodem. str. 14
Pro posouzení mezních stavů potřebujeme znát napjatost, tedy napětí v libovolném
řezu ρ vedeném daným bodem.
na
Pro určení napjatosti uvolníme prvek jedním příčným a jedním obecným řezem, jehož normála svírá se
S .
střednicí prutu úhel α; jeho plocha bude Sρ = cos
α
V příčném průřezu uvolněného prvku působí napětí
σ = p a v průřezu ρ působí soustava vnitřních elementárních plošných sil fρ dSρ rovnoběžných s osou x.
f~ρ je obecné napětí a v důsledku homogenní napjatosti prutu můžeme předpokládat, homogenní
že je po řezu ρ rozloženo rovnoměrně. Z podmínky statické rovnováhy plyne
napjatost
str. 14
X
S
Fx = 0 :
−σS + fρ Sρ = 0 ⇒ fρ = σ = σ cos α.
Sρ
Obecné napětí fρ rozložíme do významných směrů průřezu ρ, a tím dostaneme jeho
složky
– normálovou:
σρ = fρ cos α = σ cos2 α = σ2 (1 + cos 2α),
– smykovou:
τρ = fρ sin α = σ sin α cos α = σ2 sin 2α.
Tyto vztahy vyjadřují závislost obecného napětí fρ a jeho složek σρ a τρ na napětí σ
v příčném průřezu a na poloze řezu ρ vzhledem ke střednici prutu. Napjatost v prutu
je tedy napětím σ určena, protože z něj lze určit napětí v libovolném řezu ρ.
na
Z rozboru těchto vztahů vyplývá:
a) α = 0o
σρ = σ τρ = 0
b) α = 90o σρ = 0 τρ = 0
c) α = 45o σρ = σ2 τρ = σ2 = τex
zde je extrémní smykové napětí
Je vidět, že existují 2 řezy, v nichž je smykové napětí rovno nule, tj. řezy svírající se
střednicí úhel 0o a 90o . Pokud bychom řez otáčeli kolem všech os v prostoru, nalezli
bychom ještě další roviny s nulovým smykovým napětím. Jednou z nich je přímo rovina nákresny na uvedených obrázcích. Je tedy zřejmé, že existují 3 vzájemně kolmé
roviny, v nichž je smykové napětí rovno nule. Tyto roviny se nazývají hlavní roviny
napjatosti. Normálová napětí v těchto rovinách se nazývají hlavní napětí, značíme
je σ1, σ2 , σ3 a řadíme podle velikosti tak, aby platilo σ1 ≥ σ2 ≥ σ3 . Směry těchto napětí
jsou dány průsečnicemi hlavních rovin a tvoří tzv. hlavní souřadnicový systém. Jeho
předností je zjednodušení tenzoru napětí do tvaru
napjatost
na
str. 98
σ1 0 0
tenzor napětí na
T σ = 0 σ2 0 ,
str. 14
0 0 σ3
v němž je napjatost dána pouze třemi nezávislými složkami hlavních napětí. Zbývající
tři složky tenzoru napětí definují polohu hlavního souřadnicového systému, která však
u homogenního izotropního materiálu není podstatná. Pro vyšetřovanou jednoosou
57
σ1 = σ = N
S,
σ3 = σ = N
S < 0.
tahovou napjatost platí
σ1 = σ2 = 0,
σ2 = σ3 = 0, pro napjatost tlakovou je
11.9.1. Grafické znázornění napjatosti
Umožňuje názornou představu o napjatosti a snadné určení extrémních hodnot složek obecného napětí. Pro jeho odvození využijeme vztahů pro napětí v řezu ρ, jehož
normála svírá se střednicí prutu úhel α:
σρ = σ cos2 α,
τρ =
σ
sin 2α.
2
Rovnice upravíme
σρ = σ
σ σ
1 + cos 2α
= + cos 2α
2
2
2
⇒
σρ −
σ
σ
= cos 2α,
2
2
τρ =
σ
sin 2α
2
umocníme a sečteme:
2
2
2
σρ − σ2 + τρ2 = σ2 cos 2α + σ2 sin 2α
2
2
σρ − σ2 + τρ2 = σ2 (cos2 2α + sin2 2α)
2
2
σρ − σ2 + τρ2 = σ2
V této rovnici jsou jen dvě proměnné veličiny (σρ, τρ ), které můžeme použít jako základ
souřadnicového systému, tvořícího Mohrovu rovinu napjatosti.
Mohrova rovina napjatosti je rovina, na jejíž souřadné osy vynášíme napětí normálové σρ a smykové τρ působící v jistém řezu ρ vedeném vyšetřovaným bodem.
Odvozená rovnice je rovnicí kružnice ((x − m)2 + (y − n)2 = r2 ) v Mohrově rovině
napjatosti se středem na ose σρ ve vzdálenosti σ2 od počátku a s poloměrem r = | σ2 |.
Nazývá se Mohrova kružnice napjatosti
prostého tahu (σ > 0) resp. tlaku (σ < 0).
Bod na Mohrově kružnici (se souřadnicemi σρ , τρ )
znázorňuje obecné napětí fρ v bodě rovinného
řezu určeného úhlem α. Celá kružnice tedy znázorňuje napětí ve všech řezech, které můžeme vést určitým bodem prutu, tj. napjatost
v tomto bodě při prostém tahu (tlaku). Je důležité si uvědomit, že průvodič bodu Mohrovy kružnice vedený z jejího středu opisuje dvojnásobný
úhel (2α) než je úhel odklonu normály řezu α od
střednice prutu (plyne z odvození, v němž figuruje
úhel 2α).
Z Mohrovy kružnice jasně vyplývá:
– Průsečíky Mohrovy kružnice s vodorovnou osou určují velikosti hlavních napětí.
V bodu C (2α = 0o , rovinný řez kolmý ke střednici) a v bodu D (2α = 180o ,
tj. rovinný řez rovnoběžný se střednicí) jsou smyková napětí nulová.
– Maximální smykové napětí τmax je v řezu pod úhlem 45o (2α = 90o ) a má velikost
τmax = σ2 .
58
– Ve dvou protilehlých bodech A, B Mohrovy kružnice jsou smyková napětí stejně
velká, ale s opačnými znaménky. Těmto bodům v prutu odpovídají složky napětí
ve dvou vzájemně kolmých rovinných řezech ρ (dán úhlem α) a ρ′ (dán úhlem β)
– viz následující obrázek.
Stejný závěr získáme i analyticky. Bodem
střednice vedeme řez ρ daný úhlem α a k
němu kolmo řez ρ′ daný úhlem β.
β=
π
+ α,
2
2β = π + 2α,
sin 2β = − sin 2α,
σ
σ
τβ = sin 2β = − sin 2α = −τα
2
2
Tento vztah vyjadřuje větu o sdruženosti smykových napětí:
sdruženost smykových napětí
Smyková napětí ve dvou vzájemně kolmých řezech vedených bodem tělesa jsou stejnéna str. 14
velikosti a směřují buď obě do průsečnice řezů anebo od ní.
Závěry i rovnice odvozené z Mohrova diagramu napjatosti jsou znaménkově v rozporu se
závěry vycházejícími z rovnic statické rovnováhy elementárního prvku. Tento rozpor je konvence
obsažen v samotném Mohrově zobrazení, protože sdružená smyková napětí v Mohrově str. 14
diagramu mají rozdílná znaménka. To vyžaduje zavedení odlišné znaménkové konvence
pro smyková napětí v Mohrově rovině:
na
Smykové napětí považujeme za kladné, jestliže má
smysl vnější normály řezu ~en pootočené o 90o ve smyslu
pohybu hodinových ručiček.
11.10. Oblasti použitelnosti prostého tahu prutů
Prostá pružnost prutů vychází
– z prutových předpokladů,
– ze statické rovnováhy prvku v nedeformovaném stavu.
Tyto dva základní výchozí předpoklady umožnily odvodit jednoduché vztahy pro popis
napjatosti a deformace prutů. Při řešení praktických problémů s využitím teorie prosté
pružnosti je důležité posouzení její použitelnosti. Toto hodnocení vyžaduje širší znalosti, protože téměř vždy dochází k určitému porušení výchozích předpokladů. Proto
se v základním kurzu omezíme jen na kvalitativní posuzování použitelnosti, zejména
z hlediska splnění prutových předpokladů.
prutové předpoklady na str. 36
59
11.10.1. Vliv proměnnosti průřezu podél střednice prutu
a) Spojitě proměnný příčný průřez
Uvažujme přímý prut kruhového příčného
průřezu, který se podél střednice spojitě
mění. Kuželovitost prutu je dána úhlem α
mezi površkou a osou kužele. Prut je zatížen
na koncích silou F~ , tzn. jediným VVÚ po celé
délce střednice je konstantní normálová síla
o velikosti N = F a prut je namáhán tahem.
Z prutu uvolníme dvěma limitně blízkými příčnými řezy jednonásobně elementární prvek Ω1 o délce dx. Z něj dále uvolníme prvek Ω2 válcovým řezem s osou na střednici
prutu a s podstavou o ploše S1 . Na čelní stěně prvku Ω2 působí normálová napětí σ.
Aby tento prvek byl ve statické rovnováze, musí na válcovém řezu působit smyková
napětí τ . Podle věty o sdruženosti smykových napětí pak budou stejně velká smyková
napětí působit i v příčných průřezech. Předpokládáme-li podobně jako u prizmatického
prutu konstantní rozložení napětí σ v příčném průřezu S2 resp. dS, pak podmínka statické rovnováhy je
X
Fx = 0 :
σdS − τ 2πrdx = 0
Plochu dS lze zjednodušeně vyjádřit jako dS = 2πrdr, čímž dostáváme
σ2πrdr = τ 2πrdx
⇒
dr
τ
=
σ
dx
Smykové napětí je tedy přímo úměrné poměrné změně tloušťky prutu, vyjádřené pro
kuželový prut poměrem dr/dx.
Vlivem smykového napětí působícího v příčných průřezech je porušena jednoosost tahové napjatosti, následkem je jejich borcení (deplanace). Nezůstávají tedy rovinné a neprutové předpo- platí pak přesně prutové předpoklady. Odchylky jsou tím větší, čím větší jsou změny
klady na str. 36 průměru prutu. Aby smykové napětí bylo alespoň o řád menší než napětí normálové
a odchylku od prutových předpokladů bylo možné zanedbat, musí platit dr/dx < 0, 1,
tedy kuželovitost prutu α musí být menší než 0,1 rad ≈ 6o . Tuto mezní hodnotu lze
řádově brát i pro jiné tvary příčných průřezů.
Pozor! Smyková napětí jsme odvodili za předpokladu, že v průběhu zatěžování zůstávají příčné průřezy rovinné. V důsledku působení τ však nezůstanou rovinné, takže ani
smyková napětí neodpovídají přesně odvozenému vztahu.
b) Náhlé změny příčného průřezu (vruby)
vruby:
(
konstrukční - vytvářeny účelově, jsou funkční
(drážky, zápichy, otvory, osazení)
defekty
- důsledek reálné výroby
(vměstky, bubliny, trhliny)
V místech vrubů vzniká většina provozních lomů. Bylo zjištěno a lze dnes snadno doložit
výpočty s využitím MKP, že
– vruby způsobují místní koncentraci přetvoření a tím i koncentraci napětí (v blízkém okolí vrubu není v příčném průřezu prutu napětí rozloženo rovnoměrmě);
– lokálně se mění napjatost tělesa, v okolí vrubu vzniká obecná trojosá napjatost;
60
– čím menší je poloměr zaoblení vrubu, tím je vyšší extrémní napětí v kořeni vrubu,
– vrubový účinek má výrazně lokální charakter.
Pro usnadnění pevnostního posuzování vrubů byla vypracována metodika založená na
korekci prosté pružnosti prutů, která určuje extrémní hodnoty napětí v kořeni vrubu σex
z nominálního napětí σn pomocí součinitele koncentrace napětí α = σex /σn .
Nominální napětí σn = N/S je vypočteno ze vztahů napětí na str. 54
prosté pružnosti a pevnosti, tj. z předpokladu rovnoměr- α
grafy
na
ného rozložení napětí po průřezu v místě vrubu.
str. 113
Hodnoty součinitelů koncentrace napětí α byly stanoveny
výpočtem za využití MKP nebo fotoelasticimetrie pro
různé tvary vrubů a různé způsoby namáhání a zpracovány do grafů. U každého grafu je obvykle uvedeno, v kterém průřezu se počítá nominální napětí σn , k němuž se
vztahuje součinitel α.
Při pevnostních výpočtech součástí s vruby je nutno důsledně rozlišovat, zda
je materiál ve stavu křehkém nebo tvárném.
Je-li materiál prutu s vrubem ve stavu křehkém, pak v okamžiku,
kdy σex = σRt, vzniká v místě koncentrace napětí křehká trhlina. Ta zvyšuje koncentraci napětí, protože má menší poloměr zaoblení svého kořene než
konstrukční vrub. Při zatížení se pak trhlina nekontrolovaně šíří až do porušení křehkým lomem. Proto nelze připustit, aby špička napětí dosáhla meze
křehké pevnosti.
Je-li materiál prutu s vrubem ve stavu houževnatém, pak v okamžiku, kdy je
splněno σex = σK , dochází v místě koncentrace napětí ke vzniku plastických
deformací. Ty sníží koncentraci napětí (napětí nemůže výrazně překročit
mez kluzu) a zvýší koncentraci přetvoření - dojde k otupení špičky vrubu.
σRt na str. 35
σK na str. 33
Vliv vrubu je tedy nutno vždy zhodnotit z hlediska možnosti křehkého chování. Vznik trojosé napjatosti v okolí kořene vrubu může vést ke vzniku křehkého lomu i u materiálu, který se v případě hladké zkušební tyče choval jako
houževnatý!
Pokud se na základě rozborů a zkušeností vyloučí možnost křehkého porušení, je možné
volit bezpečnosti nízké (např. 1,5), protože další záloha únosnosti prutu je v plastické bezpečnost
oblasti. Protože však zatížení většiny strojních součástí není statické, ale časově proměnné, může tato opakovaná plastická deformace vést k únavovému porušení. Posouzení rizika únavového lomu však vyžaduje použití jiných postupů, které nejsou součástí
tohoto kurzu. V případě křehkého materiálu bývá volena bezpečnost vůči meznímu
stavu křehké pevnosti až kR ∈ (10; 15).
Vrub jako náhlá změna příčného průřezu
– je podstatný z hlediska napjatosti a porušování,
– je většinou nepodstatný z hlediska deformačních charakteristik prutu.
11.10.2. Vliv šroubovitosti prutu
Prut považujeme za šroubovitý, jestliže hlavní centrální osy příčných průřezů nejsou
vzájemně rovnoběžné. Šroubovitý prut lze vytvořit tak, že neměnný průřez se kolem
61
deformační charakteristiky na
str. 18
hlavní osy
str. 38
střednice posouvá a zároveň rotuje. Šroubovitost prutu můžeme kvantitativně vyjádřit
na veličinou dϕ/dx, kde ϕ je úhel natočení hlavních centrálních os vzhledem k osám výchozího průřezu. Šroubovitost, podobně jako kuželovitost, způsobuje vznik smykových
napětí v příčných průřezech. Bude-li změna polohy sousedních průřezů (charakterizovaná poměrem dϕ/dx) dostatečně malá, bude i smykové napětí oproti normálovému
zanedbatelné (τ ≪ σ). Pak můžeme použít vztahů pro prostý tah.
11.10.3. Proměnnost VVÚ podél střednice přímého prutu
Proměnnost normálové síly může být způsobena buď působením osamělých sil nebo
spojitého zatížení (objemových sil).
a) zatížení v izolovaných řezech
Pokud v ose prutu působí osamělé síly, je použitelnost modelu omezena následovně:
Saint Venantův
princip na str. 15
prutové předpoklady na str. 36
– prutové předpoklady jsou splněny až v dostatečné
vzdálenosti (ve smyslu Saint Venantova principu) od
náhlých změn zatížení, v jejichž okolí je vždy nehomogenní napjatost,
– osamělé síly v praxi nelze zavést, aniž by vznikl vrub
(otvor, osazení, drážka) nebo porušení předpokladu
o prutové napjatosti (sevření do kleštin - tlak v příčném směru nelze do teorie prutů zahrnout).
b) zatížení objemovými silami
Uvažujme prizmatický prut v silovém poli s intenzitou rovnoběžnou s osou prutu.
Priklad 402
Priklad 404
Praktická aplikace: a) prut svislý ⇒ tíhové pole,
b) prut rotující okolo osy kolmé na střednici⇒ pole odstředivých
sil.
Normálová síla a napětí jsou podél střednice proměnné, ale napětí je v průřezech rozloženo rovnoměrně. Je tedy použitelná prostá pružnost prutů (smykové napětí není
podstatné).
Napětí, posuv v bodě R střednice a energii napjatosti prutu délky l počítáme podle
vztahů, respektujících proměnnost normálové síly:
N(xR )
σ(xR ) =
,
S
u(xR ) =
ZxR
0
N(x)
dx,
ES
62
W (l) =
Zl
0
N 2 (x)
dx.
2ES
11.10.4. Zakřivení střednice prutu
Budeme uvažovat prut, jehož střednice je spojitá a hladká křivka. Charakter namáhání
prutů se zakřivenou střednicí závisí na
zakřivené pruty
na str. 84
kombinované
namáhání
na
str. 41
– tvaru střednice prutu (typ
křivky, rovinnost, prostorovost, otevřenost, uzavřenost),
– vztahu velikosti poloměru křivosti střednice k charakteristickému rozměru příčného
průřezu (slabě a silně zakřivené pruty),
– typu silové soustavy působící
na prut.
U zakřiveného prutu nemůže nastat prostý tah, ale vždy nastane kombinované namáhání.
Existuje však zakřivený prut, který lze přibližně řešit jako prut zatížený prostým tahem
– rovinný tenkostěnný kroužek (prstenec), rotačně symetricky zatížený. Zatížení může
být dvojího typu:
a) rovnoměrným tlakem na vnitřní nebo vnější povrch, např. nalisovaný kroužek
(kroužek nasazen na jiné rotačně symetrické těleso s přesahem),
Příklad 405
b) odstředivými silami, tj. rotující kroužek.
Příklad 413
Příklad 412
Jde tedy o rotačně symetrickou úlohu. Na základní
prvek Ω1 uvolněný z kroužku budou působit rotačně
symetrické složky napětí:
– v příčných průřezech obvodová napětí σt ,
– na válcových řezech radiální napětí σr .
U tenkostěnných kroužků (h ≪ R) lze napětí σr
vzhledem k napětí σt zanedbat, takže jediným významným napětím pak je napětí σt , které bude po
průřezu přibližně konstantní a vzniká zde přibližně
jednoosá homogenní napjatost jako u prostého tahu.
homogenní
napjatost
na
str. 14
tah na str. 54
Oba případy zatížení lze řešit stejným postupem, pouze u zatížení odstředivými silami
je zahrneme v duchu d’Alembertova principu do rovnice statické rovnováhy prvku Ω1
v radiálním směru:
dF − 2N sin
dϕ
=0
2
sin
dϕ . dϕ
dF
=
⇒N =
2
2
dϕ
63
zatížení tlakem p~
rotující kroužek
dFp = pdS = pbRdϕ
dFp
= pbR
Np =
dϕ
N
N
σtp = Sp = p = pR
bh
h
dFo = dmaω = ρRdϕbhω 2 R
No = dFo = ρR2 bhω 2
dϕ
N
o
σto = S = No = ρ(Rω)2
bh
Změnu poloměru střednice R (posuv v radiálním směru) určíme z obvodového přetvoření (je homogenní z důvodu osové symetrie):
εt =
2π(R + ∆R) − 2πR
∆R
=
2πR
R
Protože napjatost je jednoosá, platí zjednodušený tvar Hookova zákona
εt =
σt
E
⇒
∆R = R
σt
E
11.11. Řešení úlohy PP u prutů namáhaných prostým tahem
(tlakem)
11.11.1. Volný prut
Odvodili jsme vztahy pro výpočet napětí, energie napjatosti a deformačních posuvů
prutové předpo- prutu namáhaného prostým tahem (tlakem) při splnění prutových předpokladů:
klady na str. 36
N(xR )
σ(xR ) =
,
S(xR)
u(xR ) =
ZxR
0
N(x)
dx,
ES(x)
W (l) =
Zl
0
N 2 (x)
dx.
2ES(x)
Jsou-li veličiny N(x) a S(x) a tedy i σ(x) konstantní podél střednice, je integrace
triviální.
64
Jsou-li N(x) a S(x) proměnné (ovšem tak, že namáhání lze považovat za prosté), pak musíme obecně
střednici prutu rozdělit na intervaly, v nichž každá veličina je vyjádřena jediným funkčním vztahem. Hranice těchto intervalů jsou pak v těch bodech střednice, v nichž dochází ke změně funkce popisující zatížení nebo příčný průřez. Posuv určitého bodu střednice je algebraickým součtem prodloužení jednotlivých úseků, na které jsme rozdělili střednici prutu od
vztažného bodu.
Tato prodloužení mohou být od silového působení
u(xR) =
ZxR
0
N(x)
dx.
ES(x)
V případě teplotního zatížení se k nim přičítá teplotní dilatace
uT (xR) = α∆T xR,
kde α je součinitel teplotní roztažnosti.
Ze všech možných mezních stavů se v tomto kurzu omezíme na
– mezní stav deformace - funkčně přípustná deformace se mění na funkčně nepřípustnou, mezními hodnotami jsou mezní posuvy bodů střednice ev. mezní
úhly natočení v těchto bodech. Bezpečnost vůči meznímu stavu deformace je
dána poměrem mezní ku provozní hodnotě deformačního parametru kD = uuM
ϕ
resp. kD = ϕM .
– mezní stav pružnosti - po překročení vznikají makroplastické deformace, mezní
hodnotou je mez kluzu σK , která se určuje experimentálně. Bezpečnost vůči meznímu stavu pružnosti kK = σK .
|σ|
MS deformace
na str. 6
MS pružnosti na
str. 6
bezpečnost
Bezpečnost vůči meznímu stavu pružnosti kK se vztahuje k jednomu bodu prutu. Proto
obecně v každém bodě prutu bude její hodnota různá, tedy
kK = kK (x, y, z),
(x, y, z) ∈ Ω.
Pro posuzování spolehlivosti prutu je třeba nalézt bod, kde je kK minimální, a příčný
průřez, který obsahuje tento bod. Pro ně se používají názvy:
nebezpečný bod prutu - bod prutu, v němž je kK nejmenší,
nebezpečný průřez prutu - příčný průřez, který obsahuje nebezpečný bod.
Bezpečnost kK prutu je pak bezpečnost určená v jeho nebezpečném bodě.
Jelikož u prostého tahu (tlaku) jsou napětí σ po průřezu rozdělena rovnoměrně, nebezpečnými body jsou všechny body nebezpečného příčného průřezu.
11.11.2. Vázaný prut
V blízkém okolí vazby existuje oblast, kde není prut namáhán prostým tahem, protože se nepodaří realizovat vazbu tak, aby nebyly
porušeny v jejím okolí prutové předpoklady. V této oblasti jsou extrémní napětí vyšší než vypočtené teorií prostého tahu. Pokud je
potřebujeme znát přesněji, použijeme např. MKP.
65
prutové předpoklady na str. 36
MKP na str. 110
Postup při řešení vázaných prutů
uvolnění
na
str. 126
podmínky SR na
str. 123
statický rozbor
na str. 128
Priklad 403
částečné uvolnění na str. 43
Příklad 414
Příklad 417
Příklad 418
Příklad 437
Příklad 408
deformace
str. 18
na
posuv na str. 56
Castiglianova
věta na str. 26
1. Prut úplně uvolníme a v místě odstraněných vazeb zavedeme stykové výslednice.
2. Sestavíme použitelné podmínky statické rovnováhy. Jedinou netriviální podmínkou
P
statické rovnováhy je silová podmínka v ose x ( Fx = 0).
3. Určíme stupeň statické neurčitosti s = µ − ν. Mohou nastat tyto případy:
a) s = 0 – prut je uložen staticky určitě – pokračujeme bodem 7, body 4 – 6
vynecháme.
b) s ≥ 1 – prut je uložen staticky neurčitě – pokračujeme bodem 4.
4. Prut částečně uvolníme a sestavíme vazbové deformační podmínky, které jsou
u prutů namáhaných tahem (tlakem) určeny posuvem tolika bodů střednice, kolikrát je uložení staticky neurčité.
5. Vazbové deformační podmínky vyjádříme pomocí silového a teplotního působení
se zohledněním výrobních nepřesností (přesahy nebo vůle). Deformační podmínky
mohou být
a) homogenní – kinematický vazbový parametr má nulovou hodnotu,
b) nehomogenní – kinematický vazbový parametr má nenulovou hodnotu v důsledku výrobních nepřesností (např. montážní přesah nebo vůle vymezené před
svařením) nebo teplotní dilatace,
c) podmíněné – podle velikosti posuvu může prut zůstat buď staticky určitý nebo
se stát staticky neurčitým (např. montážní vůle způsobí nefunkčnost vazby).
Musíme určit, který z těchto možných stavů se uskuteční.
Poznámka: v případě kombinace tuhých a pružných vazeb je třeba při částečném
uvolnění zachovat tuhou vazbu (těleso zůstává jako celek vázáno nepohyblivě) a pro
sestavení nehomogenních deformačních podmínek uvolňovat vazby pružné; jinak
by těleso nebylo vázáno nepohyblivě a nastal by problém s odlišením deformačních
posuvů od pohybu tělesa jako celku.
6. Sestavíme soustavu rovnic, tvořenou podmínkami statické rovnováhy úplně uvolněného prutu a vazbovými deformačními podmínkami částečně uvolněného prutu.
Deformace je nutno vyjádřit jako funkce silových účinků pomocí vztahů pro posuv
bodu střednice nebo Castiglianovy věty.
7. Řešíme sestavenou soustavu rovnic – určíme všechny silové vazbové parametry.
8. Řešíme napjatost a deformaci stejně jako u volného prutu.
11.11.3. Soustavy s pruty namáhanými prostým tahem (tlakem)
Modelové soustavy s pruty můžeme rozdělit do 3 skupin:
vazby na str. 126
prutová
soustava na str. 130
a) soustavy sestavené pouze z prutů, z nichž každý je vázán rotační vazbou k základnímu tělesu,
b) soustavy tvořené pruty vázanými rotační vazbou s tuhými tělesy (jejichž deformace
jsou oproti deformacím prutů zanedbatelné),
c) prutové soustavy, které jsou výpočtovým modelem příhradové konstrukce (konstrukce železničních mostů, jeřábové věže, atd.).
66
Tyto soustavy bývají v praxi provedeny s nepohyblivými vazbami, nikoliv rotačními. vazby na str. 126
Výpočtový model s rotačními vazbami lze pro tyto soustavy použít jen tehdy, jestliže
momenty ve vazbách jsou zanedbatelné, k čemuž je nutné splnění těchto podmínek:
– pruty jsou přímé a štíhlé (tj. délka nejméně o řád větší než tloušťka),
– pruty jsou zatíženy pouze silami ve styčnících nebo na tuhém tělese (aby nenastal
významný ohyb),
– soustava zůstane po zavedení rotačních vazeb nepohyblivá (tj. staticky určitá nebo
neurčitá).
Za uvedených podmínek představuje každý prut binární nezatížený člen (člen pouze se
dvěma vazbami k okolí), jehož vazby k ostatním prutům, resp. fiktivním styčníkovým
tělesům (styčníkům) i k základnímu tělesu jsou rotačními kinematickými dvojicemi
(u prostorových úloh sférickými). Z rovnováhy každého takového prutu potom plyne,
že obě vazebné síly působící na prut musejí být stejně velké a jejich nositelky totožné
se střednicí prutu. Těmto dvěma silám budeme říkat prutové síly. Vzhledem ke stejné
velikosti představují tyto dvě síly společně jediný neznámý parametr.
Na základě uvedených skutečností lze pojem prutová síla“ vymezit takto:
”
Prutová síla je označení pro každou ze dvou stejně velkých vnějších vazebných sil působících na přímý prut a ležících na společné nositelce totožné se střednicí prutu, jestliže
další vnější zatížení prutu je zanedbatelné. Prutová síla (vnější) vyvolává v prutu stejně
velkou normálovou sílu N (vnitřní), takže prut je namáhán pouze tahem (je-li N kladná)
nebo tlakem (je-li N záporná).
Uvolnění prutů za těchto podmínek již není třeba provádět a uvolňujeme pouze styč- uvolnění prutu
níky.
na str. 130
a) Soustavy prutů vázaných k základnímu tělesu
Graficky znázorníme pouze uvolnění styčníku. Protože orientaci kladné prutové
síly volíme vždy tak, že je orientována ven z prutového tělesa (v prutu předpokládáme tah), budou kladné prutové síly orientovány ven ze styčníku (podle zákona
akce a reakce).
i) Soustava staticky určitá
Z rovnic statické rovnováhy styčníku určíme stykové síly, které jsou rovny normálovým silám v jednotlivých prutech.
Příklad 422
Příklad 415
ii) Soustava staticky neurčitá
Postupujeme podle obecného algoritmu řešení staticky neurčitých úloh, uvedeného pro jeden prut v předchozí kapitole.
Příklad 426
Příklad 427
Příklad 430
67
Příklad 409
napětí na str. 54
energie napjatosti na str. 55
posuv na str. 56
Castiglianova
věta na str. 26
Známe-li normálové síly v prutech můžeme určit napětí v prutech, energii napjatosti soustavy, posuvy styčníku. Pro posuvy styčníku je nutno téměř vždy použít
Castiglianovu větu. Energie napjatosti však musí být určena pro celou soustavu.
Energie napjatosti i-tého prutu délky li zatíženého prostým tahem je
W
(i)
Zli
=
0
Ni2 (x)
dx.
2Ei Si (x)
Tedy posuv uJ působiště síly F~J , působící na prut o délce li , ve směru této síly je
∂W
uJ =
=
∂FJ
Zli
0
N(x) ∂N(x)
dx.
ES(x) ∂FJ
Protože u soustav s pruty je N(x), E(x) i S(x) po celé délce jednotlivých prutů
konstantní, bude energie napjatosti soustavy tvořené n pruty
W =
n
X
W (i) =
i=1
n
X
i=1
Ni2 li
2Ei Si
a posuv uJ působiště osamělé síly F~J ve směru této síly je
uJ =
Příklad 434
Příklad 435
Příklad 410
deformační podmínky na str. 43
napětí na str. 54
energie napjatosti na str. 55
posuv na str. 56
prutová
soustava na str. 130
Příklad 308
Příklad 416
Příklad 420
Příklad 421
n
X
∂W
Ni li ∂Ni
=
.
∂FJ
i=1 Ei Si ∂FJ
b) Soustavy prutů s tuhými tělesy
i) Soustava staticky určitá
Z rovnic statické rovnováhy tuhých těles (jejichž deformace je proti deformaci
prutů nepodstatná) určíme stykové síly, které jsou rovny normálovým silám
v jednotlivých prutech.
ii) Soustava staticky neurčitá
Úplné uvolnění provádíme uvolněním tuhého tělesa. Částečné uvolnění pro
formulaci vazbových deformačních podmínek může být libovolné, ale nejvhodnější je uvolnění prutů ve vazbách se základním tělesem, jehož deformaci neuvažujeme, takže příslušné kinematické vazbové parametry jsou nulové. Deformační podmínky mohou být homogenní, nehomogenní a podmíněné.
Známe-li normálové síly v prutech můžeme určit napětí v prutech, energii napjatosti soustavy, posuvy kteréhokoliv bodu soustavy.
c) Prutové soustavy
i) Soustava staticky určitá
U prutové soustavy, která je vně i vnitřně staticky určitá, vyřešíme normálové síly v prutech postupnou styčníkovou metodou ev. obecnou styčníkovou
metodou, tj. z rovnic statické rovnováhy styčníků.
68
uvolstr. 43
ii) Soustava staticky neurčitá
Pro určení normálových sil v prutech potřebujeme navíc s deformačních podmínek,
které vycházejí z částečného uvolnění.
a) vně staticky neurčitá
Statický rozbor:
µex = 4, ν = 3
sex = µex − ν = 4 − 3 = 1
sin = p − (2k − 3) = 5 − (2 · 4 − 3) = 0
Úloha je vně 1x staticky neurčitá
a vnitřně staticky určitá
Úplné uvolnění provádíme uvolněním
prutové soustavy od základního tělesa.
Prutovou soustavu (tvořící při vzájemné
nepohyblivosti prutů tzv. prutové těleso)
částečně uvolníme (na úroveň staticky určitého uložení vůči základnímu tělesu) a sestavíme deformační podmínky (homogenní,
nehomogenní, podmíněné).
Příklad 424
Příklad 428
Příklad 429
Příklad 425
Příklad 431
statický rozbor
na str. 130
Příklad 302
částečné uvolnění na str. 43
b) vnitřně staticky neurčitá
Statický rozbor:
µex = 3, ν = 3
sex = µex − ν = 3 − 3 = 0
sin = p − (2k − 3) = 6 − (2 · 4 − 3) = 1
Úloha je vně staticky určitá a vnitřně
1x staticky neurčitá.
Částečné uvolnění pak znamená
– uvolnění sin prutů ve styčníku,
– zavedení normálové síly na konci uvolněného prutu a síly stejně velké, opačně
orientované do styčníku, s nímž byl prut
spojen (princip akce a reakce),
– sestavení vazbové deformační podmínky v místě uvolnění prutu, která vyjadřuje vzájemný posuv obou rozpojených bodů.
deformační podmínky na str. 43
Příklad 423
c) vně i vnitřně staticky neurčitá je kombinací předchozích dvou typů statické Příklad 303
neurčitosti, musíme sestavit oba typy deformačních podmínek.
Příklad 436
Nyní nezávisle na typu statické neurčitosti vyřešíme z rovnic statické rov- napětí na str. 54
nováhy styčníků a deformačních podmínek normálové síly v prutech, z nich Castiglianova
určíme napětí v prutech. Posuvy styčníků určíme Castiglianovou větou věta na str. 64
69
z energie napjatosti celé soustavy.
70
12. Prostý krut
12.1. Definice
Prostý krut je označení pro namáhání přímého prizmatického prutu, jestliže
– jsou splněny prutové předpoklady,
– příčné průřezy se nedeformují, pouze se vzájemně natáčejí kolem střednice prutu,
prostá pružnost
– jedinou nenulovou složkou VVÚ je kroutící moment Mk ,
na str. 12
– deformace prutu jsou z hlediska statické rovnováhy prvku nepodstatné,
prutové předpo– příčný průřez je kruhový nebo mezikruhový.
klady na str. 36
Poznámky k definici
Na počátku vývoje pružnosti se neomezoval tvar příčného průřezu u prutů zatížených
krutem. Se zvyšováním rozlišovací úrovně (rozvoj měření) se ukázalo, že pouze pro
kruhový a mezikruhový průřez je s dostatečnou přesností splněn předpoklad o zachování rovinnosti příčných průřezů, u ostatních tvarů příčných průřezů dochází k jejich
deplanaci. Vztahy pro prostý krut pak neplatí; nekruhové průřezy můžeme řešit
– metodami obecné PP (pruty průřezu tvaru rovnostranného trojúhelníka, elipsy,
kruhu s excentrickým kruhovým otvorem),
– analyticky (obdélník, čtverec),
– metodou konečných prvků (jakékoliv tvary).
Na rozdíl od tahu, kdy jsme podle orientace normálové síly N rozlišovali tah a tlak,
u krutu na znaménku kroutícího momentu nezáleží, těleso z izotropního materiálu se
chová stejně pro obě orientace kroutícího momentu.
12.2. Geometrické vztahy
Protože vyšetřujeme výhradně pruty rotačně symetrických průřezů, budeme používat
válcový souřadnicový systém se souřadnicemi x, r, ϕ v axiálním, radiálním a obvodovém
směru. Z hlediska deformace elementárních prvků Ω1 a Ω3 v průběhu zatěžování lze
konstatovat:
– vzdálenost dx průřezů ψ1 , ψ2 zůstane zachována,
délkové přetvoření ve směru střednice prutu je
tedy nulové εx = 0 (za předpokladu malých deformací),
– příčné průřezy se rozměrově nemění, takže jsou
nulová i délková přetvoření v radiálním (εr = 0)
a obvodovém směru (εϕ = 0),
– v důsledku zachování rovinnosti příčných průřezů
zůstává zachován pravý úhel mezi radiálním a axiálním směrem (γxr = 0),
71
prvek na str. 10
přetvoření
na
str. 18
– v důsledku rotačně symetrického charakteru deformace
jsou nulová úhlová přetvoření γϕr = 0,
– čela prvku Ω3 se vzájemně natočí o úhel dϕ, čímž
vznikne nenulové úhlové přetvoření γxϕ , jehož rozložení
d ′ obecného
po průřezu získáme z vyjádření posuvu AA
bodu A na obecném válcovém řezu s poloměrem ρ :
d′ = dxγ
AA
xϕ a při vyjádření parametry v příčném průd
′
řezu: AA = ρdϕ.
dϕ
γxϕ dx = ρdϕ ⇒ γxϕ = ρ
⇒ γxϕ = γ = ρϑ,
dx
dϕ
kde ϑ = dx je poměrný úhel zkroucení konstantní
pro daný průřez.
U prostého krutu je jediným nenulovým přetvořením úhlové přetvoření γxϕ = γ, které
je po příčném průřezu rozloženo lineárně, s nulovou hodnotou na střednici (γ = ρϑ).
Tε na str. 18
V prutu vzniká specifický stav deformace,
0
γ
popsaný tenzorem přetvoření Tε =
2
0
označovaný
jako smyková deformace,
γ
0
2
0 0
.
0 0
12.3. Rozložení napětí v příčném průřezu
geometrické
vztahy na str. 71
napjatost
na
str. 14
sdruženost smykových napětí
na str. 14
Rozložení napětí v příčném průřezu získáme pomocí konstitutivních vztahů, které pro
hookovský materiál (homogenní, lineárně pružný) mají tvar σ = Eε pro jednoosou
napjatost a τ = Gγ pro napjatost smykovou.
Pro prostý krut platí
εx = εr = εϕ = 0 ⇒
γxr = γϕr = 0
⇒
γxϕ = γ 6= 0
⇒
σ = 0,
τxr = τϕr = 0,
τxϕ (ρ) = τ (ρ) = Gγ = Gρϑ.
U prostého krutu vznikají v příčném průřezu smyková napětí, která jsou po průřezu
rozložena lineárně, s nulovou hodnotou na střednici prutu. Normálová napětí jsou nulová.
Napjatost v bodě tělesa, určená pouze jediným smykovým
napětím, se označuje jako smyková napjatost.
Smykovému napětí τxϕ v příčném průřezu ψ odpovídá stejně
velké smykové napětí τϕx v řezu procházejícím osou prutu
(věta o sdruženosti smykových napětí):
τxϕ = τϕx = τ
tenzor napětí na Smykovou napjatost lze popsat tenzorem nastr. 14
pětí Tσ , znázornit na elementárním prvku a v MoMohrova rovina hrově rovině.
0
τ
0
na str. 100
Tσ = τ 0 0
0 0 0
72
12.4. Závislost mezi VVÚ a napětím
Závislost napětí v příčném průřezu na geometrických charakteristikách průřezu a na VVÚ určíme z jediné použitelné podmínky statické ekvivalence mezi soustavou vnitřních elementárních sil v příčném průřezu danou smykovým
~ k:
napětím τ a jejich výslednicí M
X
Mx :
Mk =
Z
dMx =
ψ
Z
τ dSρ =
ψ
Z
Gϑρ2 dS = Gϑ
ψ
Z
statická ekvivalence na str. 122
ρ2 dS = GϑJP ,
ψ
kde JP je polární kvadratický moment.
JP na str. 38
Z rovnice dále plyne
geometrické
vztahy na str. 71
napětí na str. 72
- poměrný úhel zkroucení ϑ
=
- úhlové přetvoření
γ
=
- smykové napětí
τ (ρ)
=
Mk
GJP
Mk ρ
ρϑ = GJ
P
Gγ
⇒
k
τ (ρ) = M
JP ρ
12.5. Extrémní napětí
Smykové napětí τ (ρ) = Mk ρ bude maximální na největším poloměru příčného průřezu, τ (ρ) na str. 73
JP
Mk
Mk
Mk
tedy na vnějším obvodě:
τex =
ρex =
,
=
J
JP
P
Wk
ρ ex
P .
kde jsme zavedli modul průřezu v krutu Wk = ρJex
Modul průřezu v krutu pro
– kruhový průřez
πR4
JP
JP
πR3
πD3
Wk =
=
= 2 =
=
ρex
R
R
2
16
– mezikruhový průřez
"
!4
π (R4 − r4 )
4 #
3
3
πR
r
πD
d
1 −
Wk = 2
=
1−
=
R
2
R
16
D
kvadratický moment na str. 38
POZOR! Wk není aditivní veličina na rozdíl od kvadratických
momentů (ve jmenovateli je stále ρex = R, nelze odečíst modul
průřezu v krutu Wk2 malého kruhu od Wk1 velkého kruhu).
12.6. Energie napjatosti
V lineární pružnosti se celá deformační práce mění na pružnou energii napja- lineární
pružtosti A = W .
nost na str. 25
73
prvek na str. 10 Na trojnásobně elementární prvek Ω3 délky dx působí
vnitřní elementární smyková síla τ dS~j, která při natogeometrické
vztahy na str. 71 čení prvku Ω3 o úhel dϕ vykoná práci
1
Hookův zákon
d ′ = 1 τ dSγdx.
Aτ dS = τ dS AA
2
2
na str. 23
Energie napjatosti WΩ3 prvku Ω3 (po dosazení konstiτ ) a měrná energie napjatosti Λ
tutivního vztahu γ = G
(vztažená na jednotkový objem dSdx):
WΩ3 = Aτ dS =
Λ=
tah na str. 55
τ2
WΩ3
=
dSdx
2G
τ2
dSdx,
2G
1
1
Λ = τ γ = Gγ 2 .
2
2
⇒
Poznámka:
vztah pro měrnou energii napjatosti je analogický vztahu odvozenému u prostého tahu.
Vztahy platí obecně pro smykovou napjatost. Energie napjatosti WΩ1 jednonásobně
k
elementárního prvku se pak určí integrací přes příčný průřez ψ (a dosazením τ = M
J ρ,
JP =
RR
P
ρ2 dS) podle vztahu
ψ
WΩ1 =
ZZ
WΩ3 =
ψ
ZZ
ψ
ZZ
ZZ
τ2
Mk2 2
Mk2
Mk2
2
dSdx =
ρ
dxdS
=
dx
ρ
dS
=
dx,
2G
2GJP2
2GJP2
2GJP
ψ
ψ
V prutu o délce l se pak akumuluje energie napjatosti
W (l) =
Zl
WΩ1 =
0
Zl
0
Mk2
dx.
2GJP
12.7. Vyjádření deformační charakteristiky střednice
Deformace je popsána vzájemným úhlem natočení (zkroucení) dϕ dvou limitně blízkých
ϑ(ϕ) na str. 71
příčných průřezů ψ1 a ψ2 elementárního prvku Ω1
Mk dx.
ϑ(Mk ) na str. 73
dϕ = ϑdx = GJ
P
Úhel natočení ϕ průřezu, oddělujícího konečný prvek Ω0 , je
dán integrálem po délce tohoto prvku
xRR
Mk (x)
ϕ(xR) =
dx,
xm GJP (x)
kde xR je souřadnice těžiště průřezu, jehož natočení počítáme, xm je souřadnice těžiště vztažného průřezu (obvykle
s nulovým natočením).
Je-li v určitém úseku střednice Mk (x) =konst., GJP (x) =konst. a umístíme-li počátek
souřadnicového systému do těžiště průřezu s nulovým natočením (xm = 0), pak
ϕ(xR ) =
Mk xR
,
GJP
kde GJP se označuje jako tuhost příčného průřezu v krutu.
74
12.8. Deformace příčného průřezu
U prostého krutu se rozměry ani tvar příčných průřezů nemění. Pokud by k tomu došlo, prutové předpojedná se o porušení prutových předpokladů a teorie prostého krutu neplatí (např. zbor- klady na str. 36
cení příčného průřezu ztrátou tvarové stability při kroucení tenkostěnné trubky).
stabilita na str. 7
12.9. Řešení úlohy PP u prutů namáhaných krutem
12.9.1. Volný prut
Odvodili jsme vztahy pro napětí, deformaci a energii napjatosti u prutu namáhaného
krutem při splnění prutových předpokladů.
prutové předpoPro pruty s kruhovým a mezikruhovým příčným průřezem platí:
klady na str. 36
τ na str. 73
ZxR
Zl
Mk (xR )
Mk (x)
Mk2 (x)
Mk (xR )
ϕ na str. 74
τ=
ρ; τex =
; ϕ(xR) =
dx; W (l) =
dx.
JP (xR )
Wk (xR)
GJP (x)
2GJP (x)
W na str. 73
0
0
tah na str. 64
střednice
na
Je-li Mk (x) a S(x) nebo G podél střednice prostr.
36
měnný (ovšem tak, že namáhání lze považovat za
τex na str. 73
prosté), pak je nutno i u krutu (podobně jako
nebezpečný průu namáhání tahem) rozdělit střednici prutu na inřez na str. 64
tervaly, v nichž každá veličina je vyjádřena jediným funkčním vztahem. Hranice těchto intervalů
jsou pak v těch bodech střednice, v nichž dochází
ke změně materiálových charakteristik nebo funkcí
popisujících průběh Mk (x) a příčný průřez.
U krutu jsou smyková napětí rozložena po průřezu
lineárně s extrémní hodnotou na vnějším obvodě.
Nebezpečné body jsou tedy všechny body vnějšího
obvodu v nebezpečném průřezu.
Úhel natočení příčného průřezu stanovíme
– z odvozeného vztahu pro úhel natočení průřezu, jehož těžiště má souřadnici xR :
ϕ(xR ) =
ZxR
0
Mk (x)
dx
GJP (x)
natočení
na
~
– z Castiglianovy věty – úhel natočení ϕB působiště osamělé silové dvojice MB str. 74
v rovině působení této silové dvojice je
Castiglianova
věta na str. 26
Zl
∂W
Mk (x) ∂Mk (x)
ϕB =
=
dx.
∂MB
GJP (x) ∂MB
0
∂Mk (x)
Oba vztahy jsou rovnocenné, derivace ∂M
má obvykle hodnotu ±1, takže výB
sledky se mohou lišit pouze znaménkem. Mezní stav deformace je dán dosažením MS deformace
funkčně nepřípustné hodnoty úhlu natočení ϕM , bezpečnost vůči němu určíme ze na str. 6
ϕM
vztahu kϕ = ϕmax
.
bezpečnost na
str. 103
75
τK . Zde nemůžeme
|τmax |
jako mezní hodnotu použít mez kluzu v tahu σK , ale mez kluzu ve smyku. Tato hodnota
na se v praxi neměří, ale určuje se na základě Trescovy podmínky plasticity (max τ ), ze
které plyne τK = σ2K .
Bezpečnost vůči meznímu stavu pružnosti se určí ze vztahu kK =
max τ
str. 108
12.9.2. Vázaný prut
Příklad 501
Prut namáhaný krutem bude uložen staticky určitě, jestliže je omezeno natočení příčstatický rozbor ného průřezu v jednom bodě střednice.
na str. 128
Z úplného uvolnění (pro oba uvedené případy
uložení prutu je při zatížení pouze silovými dvo~ i jediným nenulovým vazebným účinjicemi M
~ A ) vidíme, že
kem složka stykového momentu M
je pouze jedna použitelná podmínka statické rovnováhy
X
Mx = 0 :
MA −
n
X
i=1
Mi = 0
s = µ − ν = 1 − 1 = 0 ⇒ uložení staticky
určité.
Ve všech ostatních případech uložení jsou pruty namáhané krutem uloženy staticky
neurčitě.
algoritmus
str. 64
Příklad 507
Příklad 503
Příklad 505
na K řešení vázaných prutů namáhaných krutem můžeme použít algoritmus uvedený v kapitole 11.11.2 Vázaný prut. Jen je potřeba si uvědomit, že u tohoto případu
– je jedinou použitelnou podmínkou statické rovnováhy momentová podmínka k ose x, tedy
P
Mx = 0,
– vazbová deformační podmínka je
určena úhlem natočení příčného
průřezu kolem střednice prutu,
a to v tolika jejích bodech, kolikrát je uložení staticky neurčité. Deformační podmínka opět
může být homogenní, nehomogenní nebo podmíněná.
Poznámka:
V případě kombinace tuhých a pružných vazeb je třeba při částečném uvolnění zachovat tuhou vazbu (těleso zůstává jako celek vázáno nepohyblivě) a pro sestavení
nehomogenních deformačních podmínek uvolňovat vazby pružné; jinak by těleso nebylo vázáno nepohyblivě a nastal by problém s odlišením deformačních posuvů od
pohybu tělesa jako celku. Deformační podmínky vyjadřujeme pouze pomocí silového
působení, neobjeví se v nich vliv teploty a obvykle ani výrobních tolerancí. Vyskytne-li
se u staticky neurčitě uloženého prutu namáhaného krutem významná změna teploty
nebo nepřesnost délky, vyvolá vznik normálové síly a z jednoduchého namáhání se
stane kombinované (krut+tah nebo tlak).
76
– I u prutů namáhaných krutem nesmíme
zapomenout na problematiku vrubů, kde
dochází ke koncentraci napětí a přetvoření. Extrémní hodnotu napětí v kořeni
vrubu určíme ze vztahu τex = ατn ,
Příklad 502
Příklad 504
Příklad 506
kde
– α je součinitel koncentrace napětí určený z grafů, které byly vytvořeny pomocí
výpočtových (MKP), resp. experimentálních (fotoelasticimetrie) metod pro různé
tvary vrubů,
– τn je nominální napětí v místě vrubu určené pomocí teorie prostého krutu.
α
grafy
str. 113
77
na
13. Prostý ohyb
13.1. Definice
prostá pružnost
na str. 12
prutové předpoklady na str. 36
Prostý ohyb je označení pro namáhání přímého prizmatického prutu, jestliže
– jsou splněny prutové předpoklady,
– příčné průřezy se vzájemně natáčejí kolem osy ležící v příčném průřezu a následně
deformují,
~ oy , M
~ oz ,
– nenulové složky VVÚ jsou pouze ohybové momenty M
– deformace prutu jsou pro řešení statické rovnováhy prvku nepodstatné.
Poznámka: Ze Schwedlerovy věty T = dMo /dx plyne, že má-li být posouvající síla T
~ o = konst.
~ To je přesně splněno jen při zatížení silovými dvojicemi.
nulová, musí být M
~ oy , M
~ oz ), je jeho řešení
Protože u prostého ohybu jsou nenulové dvě složky VVÚ (M
složitější než u ostatních typů jednoduchého namáhání. Tento typ ohybu nazýváme
ohybem obecným (někdy šikmým nebo prostorovým).
Pro zjednodušení odvodíme veškeré vztahy pro tzv. základní ohyb, při němž je jen
jedna ze složek ohybového momentu nenulová, konkrétně pro Moy 6= 0, Moz = 0.
13.2. Geometrické vztahy
Z prutu uvolníme prvek jednonásobně elementární Ω1 a z něj trojnásobně elementární Ω3 . Prvek Ω1 se deformuje tak, že se limitně blízké příčné
průřezy ψ1 , ψ2
– natočí kolem přímky ležící v příčném průřezu,
přičemž původní délka dx prvku Ω3 se změní
o deformační posuv du,
– průřezy prutu zůstanou kolmé k deformované
střednici prutu, tj. nezmění se pravé úhly α, β
prvků Ω1 a Ω3 .
předpoklady
Protože příčný průřez podle prutových předpokladů zůstává i po natočení rovinný
prutové
na a při zvoleném základním ohybu (Moy = Mo 6= 0) se natáčí kolem přímky rovnoběžné
str. 36
s osou y, jsou posuvy du nezávislé na souřadnici y a pro jejich popis postačuje rovnice
přímky (řešíme v rovině (x, z)):
du(z) = a1 + b1z.
přetvoření
str. 18
na Těmto deformacím odpovídají složky tenzoru přetvoření:
– délkové přetvoření ve směru střednice prutu
εx (z) =
du(z)
= a + bz,
dx
– nulová úhlová přetvoření γxy = γxz = 0.
V důsledku příčné kontrakce vznikají v každém bodě prutu
různě velká příčná přetvoření εy = εz = −µεx .
U prostého ohybu jsou délková přetvoření rozložena v příčném průřezu lineárně a úhlová
přetvoření jsou nulová.
78
V každém bodě prutu tedyvzniká obecný
trojosý stav deformace, popsaný tenzorem
εx 0 0
přetvoření ve tvaru Tε = 0 εy 0 . Deformace je na rozdíl od prostého tahu tenzor přetvo0 0 εz
ření na str. 18
nehomogenní po průřezu, hodnoty jsou v každém bodě různé.
13.3. Rozložení napětí v příčném průřezu
Pro hookovský materiál (homogenní, lineárně pružný) platí stejně jako
pro přetvoření εx lineární závislost i pro normálové napětí σx :
Hookův zákon
na str. 23
σx (z) = Eεx (z) = E(a + bz).
Pro smykové napětí platí vztah
τ=
E
γ = Gγ.
2(1 + µ)
Protože γxy = γxz = 0, je i τxy = τxz = 0.
Ostatní složky tenzoru napětí (σy , σz , τyz ) jsou nulové na základě prutových předpokladů. Jediným nenulovým napětím je tedy normálové napětí σx rozložené lineárně prutové předpoklady na str. 36
v příčném průřezu.
U prostého ohybu vzniká v bodech prutu jednoosá napjatost, ale na rozdíl od prostého
tahu není homogenní.
13.4. Závislost mezi VVÚ a napětím
statická ekvivalence na str. 122
Vztah pro napětí σ(z) odvodíme z podmínek statické ekvivalence mezi soustavou elementárních plošných sil σdS~i
~ oy v příčném průřezu ψ prvku Ω0 ,
a jejich výslednicí M
které sestavíme v lokálním souřadnicovém systému podle
obrázku. Použitelné podmínky statické ekvivalence pro soustavu rovnoběžných sil v prostoru jsou tři:
ZZ
σdS = 0,
Moy =
ψ
Dosadíme
ZZ
z σdS,
ψ
Moz = −
ZZ
statické
podmínky
str. 123
y σdS = 0.
na
ψ
σ = E(a + bz):
E
ZZ
(a + bz)dS = 0
ψ
protože
RR
⇒
a
ZZ
dS + b
ψ
ZZ
zdS = 0
ψ
⇒
napětí na str. 79
centrální s.s. na
a = 0, str. 38
zdS = Uy = 0 v centrálním souřadnicovém systému.
ψ
Moy = E
ZZ
(a+bz)zdS = E(a
ψ
ZZ
ψ
zdS +b
ZZ
z 2 dS)
ψ
Dosazením a, b do vztahu pro napětí, dostáváme
79
⇒
b=
Moy
EJy
σ = E(a + bz) = E
Moy
z
EJy
⇒
σ=
Moy
z.
Jy
Vztah však platí pouze tehdy, je-li splněna i třetí použitelná podmínka statické ekvivalence, což je jedině v hlavním centrálním souřadnicovém systému
Moz = −E
hlavní centrální
s.s. na str. 38
Poznámka:
ZZ
ψ
Moy
(a + bz)ydS = −E
EJy
ZZ
yzdS =
ψ
Moy
Jyz = 0
Jy
⇒
Jyz = 0
V případě nenulového momentu Moz platí obdobný vztah pro napětí
σ=−
Moz
y.
Jz
Protože obě tato napětí mají směr osy x, je možné je v případě obecného ohybu
algebraicky sečíst:
Moy
Moz
z−
y.
σ=
Jy
Jz
Všechny tyto vztahy platí jen v hlavním centrálním souřadnicovém systému. Základní
ohyb proto nastává tehdy, je-li nositelka ohybového momentu totožná s některou z hlavních centrálních os průřezu (např. osou symetrie).
13.5. Extrémní napětí
Pro usnadnění popisu rozložení napětí v průřezu nejprve zavedeme označení neutrální
osa pro přímku, která má tyto vlastnosti:
– leží v příčném průřezu a prochází jeho těžištěm,
– ve všech jejích bodech je σ = 0, a tedy i ε = 0,
– rozděluje průřez na dvě části, z nichž v jedné působí napětí kladná a v druhé
záporná.
Ze vztahu pro napětí u základního ohybu (Moy 6= 0) je zřejmé, že neutrální osou je osa y,
která je současně nositelkou ohybového momentu. Vzhledem k lineárnímu rozložení
napětí budou jeho extrémní absolutní hodnoty v bodech od této osy nejvzdálenějších.
σmax =
Moy
zmax
Jy
80
Body s největší souřadnicí z jsou tedy nebezpečnými body. U základního ohybu
je možno zavést tzv. modul průřezu
v ohybu Wo [m3], definovaný jako podíl kvadratického osového momentu příčného průřezu vzhledem k neutrální ose
a vzdálenosti nejodlehlejšího bodu obrysové čáry od neutrální osy (Wo =
Jy /zmax ). Pak můžeme maximální napětí
vyjádřit:
σmax =
Mo
Moy
zmax =
.
Jy
Wo
POZOR! Wo není aditivní veličina!!! Např. pro mezikruhový průřez ho musíme určit odečtením osových kvadratických momentů,
zatímco zmax = D/2 se nemění!
kvadratický moment na str. 38
!4
πD4 − πd4
d
Jy
πD3
64
64
1−
Wo =
=
=
D
D
32
D
2
2
U obecného ohybu je určení extrémních napětí podstatně složitější.
13.6. Energie napjatosti
V lineární pružnosti se celá deformační práce mění na pružnou energii napjatosti A = W . V kapitole 11.6 byl pro jednoosou napjatost odvozen vztah pro energii energie napjanapjatosti trojnásobně elementárního prvku
tosti na str. 55
WΩ3 = A(σdS) = ΛdSdx =
1 σ2
dSdx.
2E
Energii napjatosti jednonásobně elementárního prvku Ω1 dostaneme integrací enerM
gie WΩ3 (do které dosadíme napětí podle vztahu σ(z) = J oy z) přes plochu ψ:
napětí na str. 79
y
WΩ1 =
ZZ
ψ
protože
RR
1 σ2
1
dxdS =
2E
2E
ZZ
ψ
2
2
Moy
Moy
2
z
dSdx
=
dx,
Jy2
2EJy
z dS = Jy . V prutu o délce l se pak akumuluje energie napjatosti daná
2
ψ
integrálem energií elementárních prvků Ω1 po délce prutu
W=
Zl
0
WΩ1 =
Zl
0
2
Moy
dx.
2EJy
Pro obecný ohyb (Moy 6= 0, Moz 6= 0) je energie napjatosti dána superpozicí příspěvků
dvou základních prostých ohybů (od složek M~oy , M~oz ):
základní ohyb
na str. 79
W =W
+W .
Moy
Moz
Vztahy platí jen pro hlavní centrální souřadnicový systém (Jyz = 0)!
81
hlavní s.s.
str. 38
na
13.7. Vyjádření deformačních charakteristik střednice
deformační charakteristiky
Při ohybovém namáhání přímého prizmatického prutu se jeho střednice ohýbá a vyprostý ohyb na tváří ohybovou čáru. Podle prutových předpokladů příčné průřezy zůstávají rovinné
a kolmé k ohybové čáře. Posuvy libovolného bodu příčného průřezu tedy můžeme urstr. 78
čit, budeme-li znát průhyby a úhly natočení v jednotlivých bodech střednice (jako
průhyby označujeme složky posuvů kolmé ke střednici), které jsou proto základními
deformačními charakteristikami prostého ohybu. Určujeme je z rovnice ohybové čáry.
prutové předpoklady na str. 36
neutrální osa na
str. 80
Jednonásobně elementární prvek Ω1 se
deformuje tak, že se dva soumezné příčné
průřezy vzájemně natočí kolem neutrální
osy o úhel dϕ. Neutrální osy v jednotlivých průřezech vytvářejí dohromady neutrální rovinu, v níž jsou napětí a přetvoření nulová. Délka trojnásobně elementárního prvku Ω3 , daná úsečkou GH,
se protažením a zakřivením prvku změní
d
na G’H’.
Pro odvození rovnice ohybové čáry budeme uvažovat základní ohyb takový,
že ohybový moment ve směru osy y je
různý od nuly, ve směru osy z roven nule
(M~oy 6= 0, M~oz = 0).
přetvoření
na
str. 18
napjatost jednoosá na str. 99
napětí na str. 79
Hookův zákon
na str. 23
Prvek Ω3 se střednicí ve vzdálenosti z od neutrální osy měl
před deformací délku rdϕ (tj. stejnou jako úsečka OA, jejíž
protažení je zanedbatelné) a po deformaci (r + z)dϕ.
Délkové přetvoření prvku Ω3 tedy je
εΩ3 =
(r + z)dϕ − rdϕ
z
=
rdϕ
r
U ohybu vzniká jednoosá napjatost, a protože uvažujeme základní ohyb od složky ohybového momentu M~oy , platí
εΩ3 =
σ
Moy
=
z.
E
EJy
M
M
Porovnáním zr = EJoy z ⇒ 1r = EJoy dostáváme křivost deformované střednice 1r ,
y
y
resp. poloměr zakřivení střednice r.
Poznámka:
Moz .
základní ohyb Analogicky pro druhý základní ohyb M~oz dostaneme vztah 1r = EJ
z
na str. 79
Moy (x)
Pokud bude výraz
podél střednice konstantní (dáno předpoklady prostého
EJy (x)
ohyb na str. 78 ohybu), bude mít zdeformovaná střednice tvar části kružnice. V praxi jsou ale daleko častější případy, kdy Mo (x) 6=konst. Důsledkem je, že 1r 6= konst. a ohybová čára
je obecná rovinná křivka. (O vlivu posouvající síly, která nutně vzniká při Mo (x) 6=
vliv T na str. 84 konst., bude pojednáno v kapitole 13.9.2.)
82
V matematice se pro křivost rovinné křivky znázorňující funkci z = z(x) odvozuje vztah
2
± d z2
±w′′
1
dx
=
=
3 ,
3
r(x)
(1 + w′2 ) 2
[1 + ( dz )2] 2
dx
kde posuv bodu střednice ve směru osy z (průhyb)
jsme označili w. Porovnáním s odvozenou křivostí
dostaneme diferenciální rovnici ohybové čáry
±w′′
Moy
.
EJy
(1 + w′2)
Jedná se o obecnou, nelineární diferenciální rovnici 2. řádu, analyticky řešitelnou jen
ve speciálních případech.
3
2
=
Pro většinu strojních součástí jsou charakteristické malé deformace. Pro úhel nato.
čení ϕ < 0, 1 rad platí w′ = tg ϕ = ϕ a w′2 < 0, 01 můžeme vůči 1 zanedbat.
Pro malé deformace dostaneme obyčejnou lineární diferenciální rovnici 2. řádu s pravou stranou, řešitelnou přímou integrací:
M
w′′ = − EJoy .
y
Záporné znaménko v rovnici je důsledkem zavedených znaménkových konvencí a orientace os.
Poznámka ke znaménku v rovnici:
Volba znaménka souvisí se znaménkovou konvencí
momentu Moy (x) a s orientací globálního souřadnicového systému. Veličiny E, Jy (x), w′2 (x) jsou
vždy kladné. Kladný ohybový moment Moy (x)
způsobuje deformaci střednice naznačenou na obrázku. Je zde zakreslen i průběh w′ (x), tj. úhlu
natočení střednice. Je zřejmé, že w′′(x) (směrnice
tečny k w′ (x)) je podél celé střednice prutu záporná. Odtud vyplývá:
pro Moy (x) > 0 je w′′ (x) < 0 a tedy bude-li osa +z orientována směrem dolů (nahoru),
M
bude ve vztahu ±w′′ = EJoy záporné (kladné) znaménko. V námi zavedené orientaci
y
souřadnicových os platí tedy záporné znaménko.
13.8. Deformace příčného průřezu
Vlivem součinitele příčné kontrakce jsou přetvoření εy , εz nenulová, takže dochází ke
změnám rozměrů příčných průřezů v důsledku deformace. Jejich určení je však obtížnější než u prostého tahu, protože stav deformace v bodech prutu je nehomogenní. Pro deformace
str. 78
83
na
praxi je tato deformace obvykle nepodstatná.
13.9. Oblasti použitelnosti prostého ohybu prutů
13.9.1. Vliv proměnnosti průřezu podél střednice prutu
a) Spojitě proměnný příčný průřez
Uvažujme prut se spojitě se měnícím příčným průřezem, ve všech průřezech je kon~ o a hlavní osy v jednotlivých průřezech jsou navzájem
stantní ohybový moment M
rovnoběžné (prut je nešroubovitý).
odvození
str. 59
na
V kapitole 11.10.1 je odvozeno, že v příčných průřezech vznikne pro
N 6= 0 smykové napětí. Podobně i pro namáhání ohybem se dá odvodit, že proměnnost velikosti příčného průřezu podél střednice prutu
způsobuje vznik smykových napětí v příčných průřezech.
Podobně jako u prostého tahu zde platí, že bude-li změna příčného průřezu malá, budou
malá i smyková napětí v poměru k napětí normálovému (τ ≪ σ) a tuto odchylku od
prutové předpo- prutových předpokladů můžeme považovat za nepodstatnou. Pro určování deformace
klady na str. 36 a napjatosti můžeme pak použít vztahy prosté pružnosti.
b) Náhlé změny příčného průřezu (vruby)
Místo největší koncentrace napětí nazýváme kořen vrubu. Hodnota maximálního navruby na str. 59 pětí se určuje pomocí vztahu σmax = ασn , kde α je součinitel koncentrace napětí,
α
grafy
na σn je nominální napětí v místě vrubu, které je vypočteno ze vztahů prosté pružnosti
a pevnosti.
str. 113
napětí na str. 79
Na příkladu průběhu napětí v místě vrubu prutu,
zatíženého v případě a) tahem a v případě b)
Příklad 602
ohybem jsou vidět odlišnosti:
1. u ohybu může existovat koncentrace napětí
současně jak v oblasti tahové, tak tlakové,
2. u ohybu má poloha vrubu vliv na koncentraci napětí (odlišný charakter koncentrace
v závislosti na poloze vrubu v příčném průřezu prutu),
3. koncentrace napětí v kořeni vrubu umístěného
v blízkosti neutrální osy nemusí u ohybu překročit nominální napětí na obvodu, zatímco u tahu,
kde je homogenní napjatost, bude napětí v kořeni
vrubu vždy největší.
13.9.2. Proměnnost ohybového momentu podél střednice
Předpoklady prostého ohybu může splnit jedině prut zatížený osamělými silovými dvojicemi, pro nějž platí
84
– posouvající síla T (x) = 0,
– ohybový moment Mo (x) = M = konst. v jednotlivých intervalech,
Pak smyková napětí v příčných průřezech nevznikají.
V praxi je daleko častější prut zatížený osamělými silami nebo spojitým liniovým zatížením v příčném směru, u nějž je posouvající síla nenulová a ohybový moment není
konstantní. Pro takovýto prut se často používá tradiční název nosník. U něj vzniká
složitější typ napjatosti:
~ o vznikají v příčných průřezech normá– od ohybových momentů M
lová napětí σ.
– od posouvající síly T~ vznikají v příčných průřezech smyková napětí τ .
Příčné zatížení vede vždy ke vzniku smykových napětí v příčných průřezech.
Velikost a rozdělení smykových napětí v příčných průřezech s obecným tvarem obrysové křivky a s obecnou polohou nositelky posouvající síly je možno stanovit metodami
obecné pružnosti nebo MKP. Na úrovni pružnosti prutů se smyková napětí určují pro
2 případy:
1. příčné průřezy alespoň s 1 osou symetrie,
2. tenkostěnné příčné průřezy – profily I, U, T za předpokladu, že
– prut je prizmatický,
– povrch prutu není zatížen smykovými silami.
V literatuře lze nalézt vztah pro výpočet smykového napětí, který se někdy nazývá Žuravského vzorec.
τ (x, z) =
T (x)Uyψ1 (z)
,
b(z)Jy
kde Uyψ1 (z) je statický moment plochy ψ1 (z) k neutrální
ose .
Tento vzorec je odvozen za předpokladu, že nositelka posouvající síly je osou symetrie
příčného průřezu a smyková napětí jsou po jeho šířce rozložena rovnoměrně. Z něj
dostaneme vztahy pro
maximální smykové napětí
a) v obdélníkovém průřezu: τmax =
3T
2S
b) v kruhovém průřezu:
4T
3S
τmax =
Poznámka:
Je tedy zřejmé, že v praxi někdy používaná hodnota tzv. smluvního smykového napětí
τs = T /S vede ke značnému podhodnocení smykových napětí. Navíc u některých profilů
85
statický moment
na str. 38
neutrální osa na
str. 80
nejsou všude splněny ani předpoklady Žuravského vztahu a extrémní smyková napětí
jsou ve skutečnosti ještě vyšší.
Castiglianova
věta na str. 26
Λ na str. 73
Pro výpočet deformačních parametrů využitím Castiglianovy věty je třeba do energie
napjatosti zahrnout i vliv posouvající síly. Pro měrnou energii napjatosti od smykoτ 2 . Jeho integrací přes průřez ψ dostaneme energii
vých napětí byl odvozen vztah Λ = 2G
napjatosti jednonásobně elementárního prvku Ω1, v jehož příčném průřezu působí smykové napětí τ vyvolané posouvající silou T~
ZZ
ZZ
2
T 2Uyψ1
(z)
1
τ2
WΩ1 =
dSdx =
dxdS.
2
2G
2G
b (z)Jy2
ψ
ψ
Vztah upravíme, zlomek rozšíříme o plochu S a výraz (v hranaté závorce), který závisí
pouze na průřezových charakteristikách a pro daný tvar průřezu je konstantní, označíme β:
WΩ1 =
Příklad 627
2
T
S
2GS
ZZ
ψ
2
Uyψ1
(z)
βT 2
dS
dx
=
dx
b2 (z)Jy2
2GS
.
Pro kruhový průřez je β = 32/27 = 1, 185 = 1, 2, pro obdélníkový β = 1, 2.
U prutu o délce l tedy posouvající síla přispěje k celkové energii napjatosti hodnotou
WT =
Zl
WΩ1
0
β
=
2G
Zl
0
T 2(x)
dx.
S(x)
13.9.3. Zakřivení střednice prutu
základní ohyb
na str. 79
neutrální osa na
str. 80
centrální osa na
str. 38
σp na str. 79
U rovinného zakřiveného prutu, namáhaného základním ohybem, jsou normálová napětí v příčném průřezu rozložena podle hyperboly s neutrální osou posunutou vůči
centrální ose, na rozdíl od prutu přímého, kde jsou rozložena podle přímky.
Pro porovnání výpočtu průběhu napětí
(u prutu s poloměrem křivosti R a rozměrem
příčného průřezu v rovině střednice h) při
použití vztahů pro pruty zakřivené σz a pro
pruty přímé σp vyneseme závislost ∆σ(R/h),
σ −σ
kde ∆σ = z σz p · 100 %.
Poměr R/h charakterizuje relativní zakřivení prutu,
∆σ je odchylka napětí σp od σz . Z grafu je patrné, že
průběh napětí u prutů slabě zakřivených, pro něž
platí h ≪ R (velké R ), je možno řešit užitím vztahu
h
pro pruty přímé. Při poměru R/h = 10 se dopustíme chyby ∼ 4%, pro R/h = 5 bude chyba cca. 8%.
Průběh napětí u prutů silně zakřivených s poměrem R/h < 5 je hyperbolický, extrémní hodnota
napětí je vyšší a musíme ji počítat pomocí vztahů
pro pruty zakřivené (ty nejsou součástí bakalářského
studia PP) nebo dnes častěji metodou konečných
prvků.
86
13.10. Řešení úlohy PP u prutů namáhaných ohybem
13.10.1. Volný prut
Odvodili jsme vztahy pro napětí, deformační parametry a energii napjatosti u prutu
namáhaného ohybem při splnění prutových předpokladů . U praktických výpočtů se prutové předpoomezíme v tomto kurzu na základní ohyb, pro nějž platí vztahy ve zjednodušené podobě klady na str. 36
σ(z) =
Mo
Moy
Moy
z; σmax =
; w′′ = −
; W =
Jy
Wo
EJy
Zl
0
2
Moy
2EJy
dx
Při vyšetřování mezních stavů deformace je třeba znát průhyby resp. úhly natočení
aspoň v některých význačných bodech střednice prutu. Pro jejich určení existuje řada
metod, z nichž si uvedeme dvě:
σ(z) na str. 79
σmax na str. 80
w′′ na str. 82
W na str. 81
– integrace diferenciální rovnice průhybové čáry prutu (diferenciální přístup),
– Castiglianova věta (integrální přístup).
13.10.2. Diferenciální přístup
Moy (x)
Diferenciální rovnice w′′ (x) = − EJ
se řeší přímou integrací. Musí být doplněna
y
okrajovými podmínkami. U prutů, u nichž průběh Mo (x) po celé délce vyjádříme jedi- Příklad 604
nou funkční závislostí (hladkou a spojitou), řešíme jednu diferenciální rovnici 2. řádu Příklad 607
a potřebujeme pro určení integračních konstant 2 okrajové podmínky.
Okrajové podmínky mohou být popsány
a) vazbovými podmínkami – známými průhyby a úhly natočení v místě vazeb prutu
se základním tělesem,
b) symetriií deformace,
pro x = 2l → w′ = ϕ = 0 (tečna k ohybové čáře je rovnoběžná s osou x)
Pro prut na obrázku máme tedy dvě možnosti pro vyjádření okrajových podmínek:
1. vazbové podmínky
2. symetrie deformace
x=0 w=0
x=0 w=0
x=l w=0
x = 2l w′ = 0
c) geometrickými prutovými předpoklady (střednice zůstává během deformace spojitá a hladká). Je-li výraz Moy /EJy vyjádřen na úsecích prutu různými funkčními závislostmi, pak na hranicích těchto úseků formulujeme podmínky spojitosti
a hladkosti střednice.
Např. pro x = a, kde je změna zatížení (změna průběhu Mo (x)), musí platit
– průhyb zleva se rovná průhybu zprava (zachování
spojitosti) ⇒ wI = wII
– natočení zleva se rovná natočení zprava (zachování
hladkosti střednice) ⇒ ϕI = ϕII
87
prutové předpoklady na str. 36
U prutů, u nichž je výraz Moy /EJy vyjádřen různými závislostmi v určitých částech
střednice, pak postupujeme následovně:
Příklad 616
materiálové charakteristiky na
str. 23
průřezové
charakteristiky
na str. 38
ohybová čára na
str. 82
Příklad 622
– Střednici rozdělíme na úseky, v nichž je výraz Moy /EJy vyjádřen jedinou závislostí. Hranice intervalů jsou v místech změny zatížení,
materiálových a průřezových charakteristik.
– Pro každý úsek napíšeme diferenciální rovnici.
– Popíšeme vazbové okrajové podmínky, vyplývající z vazeb prutu se základním tělesem.
– Pro všechna rozhraní mezi intervaly napíšeme pro deformovanou střednici
podmínky spojitosti (rovnost průhybů zleva a zprava) (wi (a) = wi+1 (a)),
podmínky hladkosti (rovnost natočení zleva a zprava) (ϕi (a) = ϕi+1 (a))
Protože k řešení diferenciální rovnice ohybové čáry je třeba stanovit 2 integrační konstanty, musíme napsat odpovídající počet (2x počet intervalů) okrajových podmínek.
Mo (x)
Pro jejich správné sestavení je nutné, aby funkce EJ
byla pro všechny úseky vyjáy
dřena v tomtéž souřadnicovém systému.
13.10.3. Integrální přístup
Castiglianova
věta na str. 26
WMo na str. 81
WT na str. 84
Deformační charakteristiky pro konkrétní body střednice můžeme také určit s využitím
Castiglianovy věty.
V prutu délky l se akumuluje energie napjatosti
W = WMoy
1
+ WT =
2E
Zl
0
l
Z
2
Moy
(x)
β
T 2(x)
dx +
dx,
Jy (x)
2G
S(x)
0
která je superpozicí příspěvků od ohybu a smyku.
Castiglianova
věta na str. 26
Příklad 625
Při řešení posuvu působiště J síly F~J dosadíme energii napjatosti do Castiglianovy věty
a v obecném tvaru zderivujeme:
∂W
wJ =
=
∂FJ
Zl
0
Moy ∂Moy
dx + β
EJy ∂FJ
Zl
0
T ∂T
dx.
GS ∂FJ
Přitom musíme mít na paměti, že průhyb wJ je globální veličinou (závisí na deformacích
celého prutu). Proto složky VVÚ musí být vyjádřeny jako funkční závislosti po celé
délce střednice prutu. U dlouhých štíhlých prutů (l > 10h) je příspěvek posouvající
síly zanedbatelný.
13.10.4. Porovnání diferenciálního a integrálního přístupu
1. diferenciální přístup:
Umožňuje:
velké deformace
na str. 82
a) řešit i velké průhyby – pomocí rovnice pro velké deformace
(pouze v určitých jednoduchých případech),
88
M
±w′′
= EJoy
′2 23
y
(1 + w )
624
b) určit v obecném místě velikost průhybu a natočení.
c) určit extrémní průhyb i v případě, že neznáme polohu extrémního průhybu.
Nevýhody: nezahrnuje vliv posouvající síly na průhyb a natočení a obvykle je
matematicky složitější a pracnější.
2. integrální přístup (Castiglianova věta):
a) umožňuje určit deformační charakteristiky v kterémkoli konkrétním bodě
střednice; pokud v něm nepůsobí odpovídající vnější zatížení, přidáme do~ d = 0, s nimiž pracujeme jako se
plňkovou sílu F~d = 0 nebo silovou dvojici M
známým vnějším zatížením,
b) umožňuje zahrnout vliv posouvající síly T~ na průhyb a natočení,
c) ve srovnání s diferenciálním přístupem je výpočet podstatně rychlejší a snazší,
d) umožňuje volit různý (optimální) souřadnicový systém v každém úseku,
e) je použitelný i u zakřivených a lomených prutů.
Nevýhody:
a) lze ho použít pouze v lineární pružnosti (malé deformace, hookovský materiál,
vazby lineární),
b) řeší deformaci v konkrétním bodě, obtížně se používá při hledání extrémů.
Příklad 618
Příklad 621
charakteristiky
na str. 18
Příklad 625
lineární
pružnost na str. 25
13.10.5. Vázaný prut
V blízkém okolí vazeb existuje oblast, kde není prut namáhán prostým ohybem, protože
se nepodaří realizovat vazbu tak, aby omezovala jen posuvy a natočení střednice. Tuto prutové předpooblast nemůžeme řešit pomocí vztahů pro prostý ohyb. Je-li tato oblast rozhodující klady na str. 36
z hlediska mezních stavů, je třeba použít např. MKP.
Postup při řešení vázaných prutů
1. Prut úplně uvolníme a v místě odstraněných vazeb zavedeme stykové výslednice.
2. Sestavíme použitelné podmínky statické rovnováhy.
3. Určíme stupeň statické neurčitosti s = µ − ν. Mohou nastat tyto případy:
a) s = 0 – prut je uložen staticky určitě – pokračujeme bodem 7.
b) s ≥ 1 – prut je uložen staticky neurčitě – pokračujeme bodem 4.
4. Prut částečně uvolníme a sestavíme vazbové deformační podmínky, které jsou
určeny posuvem ev. natočením tolika bodů střednice, kolikrát je uložení staticky
neurčité.
5. Vazbové deformační podmínky vyjádříme pomocí silového působení s využitím
Castiglianovy věty. Pokud vazby omezují podélné deformace prutu, vznikne v něm
nenulová normálová síla a z jednoduchého namáhání se stane kombinované (ohyb
+ tah nebo tlak). Deformační podmínky mohou být
a) homogenní – kinematický vazbový parametr má nulovou hodnotu,
b) nehomogenní – kinematický vazbový parametr má nenulovou hodnotu v důsledku výrobních nepřesností (např. nestejná výška podpor, nesouosost vazeb),
c) podmíněné – podle velikosti posuvu ev. natočení může prut zůstat buď staticky určitý nebo se stát staticky neurčitým (např. montážní vůle způsobí
nefunkčnost vazby).
6. Sestavíme soustavu rovnic, tvořenou podmínkami statické rovnováhy úplně uvolněného prutu a vazbovými deformačními podmínkami částečně uvolněného prutu.
7. Řešíme soustavu rovnic.
8. Řešíme napjatost a deformaci stejně jako u volného prutu.
89
uvolnění
na
str. 126
SR na str. 123
rozbor
na
str. 128
Příklad 602
částečné uvolnění na str. 43
jednoduché namáhání
na
str. 41
Příklad 617
Příklad 608
Příklad 613
14. Zakřivené a lomené otevřené pruty
prutové předpoklady na str. 36
Příklad 203
Příklad 623
Příklad 619
Příklad 620
a) Zakřivený prut je prut, jehož střednice je spojitá
a hladká křivka.
b) Lomený prut je těleso charakteru prutu, jehož střednice je spojitá, ale po částech hladká křivka. Tyto části
mohou být přímé nebo zakřivené. Lomený prut má konečný počet zlomů, v okolí zlomu nejsou splněny prutové
předpoklady, tedy okolí zlomu není možno řešit pomocí
prosté pružnosti a pevnosti.
Chceme-li řešit lomený prut, pak
Saint Venantův
princip na str. 14
1. využíváme Saint Venantův princip a jako prut
řešíme pouze části v dostatečné vzdálenosti od
míst zlomů,
2. můžeme se zabývat jen takovými lomenými
pruty, u nichž součet zlomy ovlivněných délek
střednice je malý vzhledem k celé délce střednice,
součinitel
koncentrace napětí na str. 113
3. předpokládáme, že se jedná o tzv. tuhý zlom, u nějž se zachovává úhel střednice ve
zlomu, takže se zlom natáčí jako celek. Tento předpoklad je oprávněn tehdy, pokud
je místo zlomu dostatečně vyztužené v porovnání s hladkými částmi prutu. Vyztužení je obvykle potřebné z hlediska mezních stavů, protože napjatost ve zlomu
se nedá řešit analytickým výpočtem. V některých případech je možné extrémní
napětí v okolí zlomu určit pomocí součinitele koncentrace napětí, podobně jako
u vrubu.
4. protože se limitní okolí zlomu nedeformuje (zlom se natáčí jako celek), energii
napjatosti počítáme jen pro hladké části prutu, což je oprávněné, jsou-li splněny
předpoklady podle bodů 2 a 3.
algoritmus
str. 87
Příklad 606
Příklad 609
Příklad 605
Příklad 611
Příklad 612
na Algoritmus řešení je shodný pro přímé i zakřivené pruty. Uvedeme jen několik poznámek, které si je potřeba uvědomit.
Příklad 626
Příklad 603
3. Musíme zvážit a rozhodnout, zda je možné prut řešit jako slabě zakřivený. V opačném případě nutno použít analytickou teorii zakřivených prutů, která není součástí
tohoto kurzu nebo MKP.
princip Saint Venantův na str. 15
4. Vyjde-li nebezpečné místo ve zlomu, pak ve smyslu Saint Venantova principu řešíme místo v blízkosti zlomu zleva nebo zprava, protože vlastní zlom řešit neumíme.
1. Střednice je obecně zakřivená, proto u veličin vyjádřených integrálem (deformační
parametry) je za integrálem místo dx výraz ds.
2. Má-li střednice zlomy a místa přechodů z přímých do zakřivených částí, integrujeme při výpočtu deformačních parametrů po částech.
90
vané
ní
na
5. U zakřivených a lomených prutů se vyskytuje jednoduché namáhání jen ve zvláštních případech. Převážně se jedná o namáhání kombinované, u rovinných štíhlých
prutů je často dominantním namáháním ohyb.
ohyb na str. 78
6. U staticky neurčitě uložených prutů se částečné uvolnění obvykle realizuje uvolněním vazeb k základnímu tělesu. Pro využití Castiglianovy věty je pak vždy nutné
ve vztazích pro složky VVÚ vystupující v energii napjatosti vyjádřit stykové výslednice z rovnic statické rovnováhy jako funkce té stykové výslednice, podle které
se derivuje energie napjatosti.
91
Castiglianova
věta na str. 26
Příklad 613
Příklad 614
Příklad 610
Příklad 615
15. Vzpěrná stabilita prutů
tlak na str. 53
Jedním z jednoduchých namáhání prutů, kterým jsme se zabývali, byl prostý tlak.
Z definice prostého tlaku vyplývá, že příčné průřezy se vzájemně pouze přibližují.
mezní stav na Pokud ve skutečnosti namáháme relativně tenkou tyč (postr. 7
měr charakteristického rozměru příčného průřezu k délce
prutu je malý) tlakem, začne se od určitého okamžiku tyč
prohýbat. Podstatnou deformací se stane ohyb. V průběhu zatěžování se mění charakter deformace. V počáteční fázi je podstatné stlačování střednice a nepodstatný její ohyb, při větších zátěžných silách je tomu naopak - ohyb je podstatný a nepodstatné je stlačování.
Rozhraní těchto dvou stavů označujeme jako mezní stav
vzpěrné stability.
Příklad 701
Mezní stav vzpěrné stability je stav, ve kterém se mění charakter podstatné deformace.
15.1. Vzpěrná stabilita ideálního volného prutu
Vyšetřujeme prut namáhaný na tlak za těchto předpokladů:
prutové předpoklady na str. 36
a) střednice prutu je v nezatíženém stavu ideálně přímá,
b) prut je prizmatický a nešroubový,
c) průřez prutu je tlustostěnný (tj. všechny rozměry příčného průřezu jsou řádově
stejně velké),
d) prut je zatížen dvěma rovnovážnými osamělými silami F , které působí v těžištích
čel prutu a jejich nositelky jsou totožné se střednicí prutu v nezatíženém stavu,
e) materiál prutu je homogenní, izotropní a bez omezení lineárně pružný (σK → ∞),
f) v průběhu celého zatěžování platí prutové předpoklady prostého namáhání prutů.
Splnění těchto předpokladů charakterizuje ideální tlakové namáhání ideálního prutu.
Cílem řešení je především určit, kdy podstatnou deformací prutu je jeho stlačování
a kdy ohýbání. Proto se z VVÚ omezíme na podstatné složky:
~
stlačování - normálová síla N
~o
ohýbání
- ohybový moment M
tlak na str. 53
Napjatost a deformace prutu při stlačování bez ohybu střednice byla probrána v kapitole 11. Prostý tah a tlak. Všimneme si tedy především ohybu.
92
Pro řešení je nutné použít diferenciální rovnici ohyohybová čára na
bové čáry prutu, a to ve tvaru platném pro velké
str. 82
deformace. Navíc musíme pro určení Mo uvolnit prprvek na str. 12
vek prutu v deformovaném stavu! (Při uvolnění
v nedeformovaném stavu je Mo = 0.)
V důsledku průhybu deformované střednice působí
~ i pov příčných průřezech kromě normálové síly N
~
~
souvající síla T a ohybový moment Mo . Prut je tedy
namáhán kombinací tlaku, ohybu a smyku, protože
je však dlouhý a štíhlý (jinak by nedocházelo k jeho
prohýbání), bude podstatným namáháním pouze
ohyb.
S ohledem na předpokládanou homogenitu, prizmatičnost a nešroubovitost bude ohybová čára rovinnou křivkou.
Z momentové podmínky statické rovnováhy vyjádříme Mo (x) a dosadíme do rovnice
ohybové čáry pro velké deformace:
ohybová čára na
str. 82
Mo (x) − F w(x) = 0
⇒
Mo (x) = F w(x)
Ze vztahu je vidět, že ohybový moment a tedy i napětí v prutu jsou funkcí průhybu w
a nelze tedy napětí a deformace řešit odděleně (PP II. řádu).
w′′
F w(x)
=−
′2 3/2
EJ
(1 + w )
Obecné řešení uvedené nelineární diferenciální rovnice 2. řádu obsahuje 2 integrační
konstanty, pro něž musíme napsat 2 okrajové podmínky:
x = 0
x = ld
w = 0
w = 0
Řešení rovnice s uvedenými okrajovými podmínkami je neschůdné, protože neznáme
skutečnou vzdálenost konců prutu ld , která
je menší než délka prutu l. Se zanedbáním
tohoto rozdílu (pro l = ld) řešil problém
Lagrange. My si z Lagrangeova řešení uvedeme jen výsledek ve tvaru závislosti maximálního průhybu wmax na síle F . Z obrázku
je vidět, že existuje kritická síla vzpěru Fkr
vymezující intervaly:
F
F
< Fkr
> Fkr
F
= Fkr
- prut se pouze stlačuje, průhyb je nulový,
- prut se buď jen stlačuje, a pak je v labilní rovnováze (větev 1 viz obr.),
nebo se jen ohýbá, a pak je v rovnováze stabilní (větev 2 viz obr.),
- stabilní stlačování se mění na labilní a stabilním se stává ohýbání. Je
to bod rozdvojení (bifurkace) rovnováhy.
Bod rozdvojení rovnováhy je mezním stavem vzpěrné stability ideálně namáháného
ideálního prutu.
93
Lagrangeovo řešení je matematicky velmi náročné a pro praktické použití se nehodí.
Proto vyřešíme uvedenou diferenciální rovnici průhybové křivky za předpokladu malých
.
deformací (w′ ≪ 1 ⇒ 1 + w′2 = 1). Z obrázku je zřejmé, že tento předpoklad může
platit, pokud zátěžná síla nedosáhne kritické velikosti Fkr a průhyby jsou zanedbatelné.
Tímto zjednodušeným řešením tedy nejsme schopni určit velikosti průhybů po vybočení
prutu, ale pouze velikosti kritické síly, při které k vybočení (meznímu stavu vzpěrné
mezní stav na stability) dochází. Řešíme tedy diferenciální rovnici průhybové křivky ve tvaru
str. 7
F w(x)
w′′ +
= 0.
EJ
.
Protože ld = l, okrajové podmínky vyjádříme ve tvaru
x = 0
x = l
w = 0
w = 0
F ji převedeme do normovaného tvaru
Označením p2 = EJ
w′′ + p2 w = 0,
pro nějž je známo obecné řešení, mj. v goniometrickém tvaru
w = C1 sin(px) + C2 cos(px).
Integrační konstanty určíme z okrajových podmínek:
w(0) = 0 :
w(l) = 0 :
0 = C1 sin 0 + C2 cos 0 =⇒ C2 = 0
0 = C1 sin(pl)
=⇒ C1 sin (pl) = 0
Druhá podmínka bude splněna, když
a) C1 = 0 =⇒ w = 0 s libovolným argumentem u funkce sinus =⇒ při libovolné
působící síle F zůstává prut přímý, tj. větev 1 Lagrangeova řešení (labilní rovnováha), což vlivem odchylek od ideálního prutu v praxi nenastane, ale tento nereálný
výsledek můžeme získat numerickým řešením, např. MKP.
b) C1 6= 0 =⇒ sin(pl)r= 0 =⇒ pl = kπ pro k = 0, 1, 2, . . .
2
F = kπ =⇒ F = (kπ) EJ
Dosadíme za p : l EJ
pro k = 0, 1, 2, . . .
2
l
– k=0:
F =0
prut je nezatížený a nemá tedy důvod se deformovat, proto w = 0.
2
– k=1:
F = Fkr = π EJ
6= 0 =⇒ w 6= 0 ,
l2
ale průhyb je neurčitý, protože podmínka je splněna pro jakékoli C1. Srovnáním
tohoto výsledku s obecným řešením vidíme, že souhlasí v okolí bodu Fkr pro
velmi malé průhyby, protože tečna ke křivce průhybu je v tomto bodě kolmá
na osu F . Znamená to ale, že z přibližného řešení jsme získali přesnou hodnotu
kritické síly (ovšem pro ideální a ideálně zatížený prut).
– k > 1 ⇒ F > Fkr a deformační stav (viz obr.) by byl
nestabilní, takže v praxi samovolně nenastane.
Jeho stability lze konstrukčně dosáhnout zamezením průhybů v některých bodech prutu a tím podstatně zvýšit hodnotu kritické síly. U volného prutu je
však jediným stabilním prohnutým stavem stav při Fkr .
94
Z uvedeného rozboru docházíme k tomuto závěru:
Předpokládáme-li při výpočtu průhybu ideálního prutu malé průhyby (w′2 ≪ 1), pak
dostaneme správnou hodnotu síly Fkr , při níž nastává rozdvojení rovnováhy, ale nejsme
schopni určit průhyb prutu po překročení F > Fkr .
Ještě zbývá určit, ve které rovině průhyb ideálního prutu nastane. Bude to rovina, pro kterou bude Fkr minimální, protože
v ostatních rovinách by k průhybu byla zapotřebí síla větší. A protože Fkr je přímo úměrná hlavnímu centrálnímu kvadratickému
momentu J (Fkr = π 2 EJ
), bude minimální pro J = J2 (menší
l2
z obou hlavních centrálních kvadratických momentů). To znamená, že vztažná osa momentu J2 je neutrální osou ohybu. Průhyb nastane ve směru osy J1 , protože v ostatních směrech by
nastal až při vyšší hodnotě síly. Proto pro prut s obdélníkovým
průřezem podle obrázku průhyb nastane ve směru menšího z obou
rozměrů příčného průřezu.
15.2. Kritická síla vzpěru u vázaného prutu
Doposud jsme se zabývali nejjednodušším případem - volným prutem, zatíženým dvěma
rovnovážnými silami na společné nositelce. V literatuře (např. [1]) je odvozen vztah pro
kritickou sílu pro vázaný prut ve tvaru
Fkr = α2
EJ2
l2
nebo Fkr =
π 2EJ2
.
2
lred
Veličina α je dána uložením prutu (v případě prutu volného α = π), redukovaná délka
se stanoví podle obrázku. Je to délka volného prutu, jehož kritická síla odpovídá kritické
síle zadaného vázaného prutu. Protože v koncových bodech volného prutu je nulový
ohybový moment i v prohnutém stavu, odpovídá redukovaná délka vzdálenosti dvou
nejbližších bodů s nulovým ohybovým momentem na deformované střednici prutu.
Odvozené vztahy platí pro ideální a ideálně zatížený prut, pro nějž určíme bezpečnost
vůči meznímu stavu vzpěrné stability ze vztahu
kV =
Fkr
.
F
Jsou-li odchylky od přepokladů nepodstatné, je možné použít tuto kritickou sílu i pro
posouzení bezpečnosti reálného prutu. Je ovšem třeba volit vyšší hodnoty bezpečnosti,
obvykle kV ∈ h3; 5i. Na druhé straně, jsou-li odchylky od předpokladů ideálního vzpěru
95
kvadratický moment na str. 38
neutrální osa na
str. 80
podstatné, dochází při zatěžování prutu od samého začátku ke spojitému růstu průhybu, jedná se tedy o kombinaci tlaku a ohybu - mezní stav vzpěrné stability vůbec
nenastane.
15.3. Tlakové namáhání prutu ze skutečného materiálu
napjatost
str. 98
na Až doposud jsme předpokládali, že chování materiálu při jednoosé napjatosti je popsáno
lineární neohraničenou závislostí σ = Eε a nevznikají tedy ani plastické deformace, ani
porušení spojitosti (lom) prutu. Nejjednoduššími výpočtovými modely skutečného materiálu jsou buď materiál houževnatý s výraznou mezí kluzu σK nebo materiál křehký,
křehký lom na u něhož při |σ| = σRd nastává náhle křehký lom. Napětí v bodě rozdvojení rovnováhy
str. 7
má velikost
|N|
Fkr
EJ2
E
l
l
σkr =
=
= α2 2 = α2 2 , kde λ = r
=
je tzv. štíhlost prutu.
S
S
l S
λ
i
J2
S
r
Veličina i = J2 se nazývá poloměr osového kvadratického momentu a slouží pro
S
porovnání tloušťky prutů při různých tvarech jejich průřezů.
Závislost tlakového napětí σkr v bodě rozdvojení rovnováhy na štíhlosti prutu λ je
hyperbolou vyššího stupně (Eulerova hyperbola). Odvozený vztah pro kritickou sílu
vzpěru platí jen tehdy, je-li σkr menší než mez lineárního chování materiálu. Rovnosti
obou těchto hodnot odpovídá kritická štíhlost prutu, kterou označíme λR nebo λK
podle typu chování materiálu.
a) Křehký materiál:
Vybočení prutu může nastat, pokud σRd > σkr = α2 E2 , tj. pro štíhlost prutu
λ
r
E
λ > α σRd = λR . Pro λ < λR nastává porušení prutu křehkým lomem.
b) Houževnatý materiál:
Pružný vzpěr může nastat, pokud σK > σkr = α2 E2 , tj. pro štíhlost prutu
λ
r
E
λ > α σK = λK . Pro λ < λK nastává mezní stav pružnosti prutu dříve než mezní
stav vzpěrné stability. I pak může nastat ztráta vzpěrné stability, ale jedná se již
o chování pružně plastické, pro něž odvozené vztahy neplatí.
Příklad 702
Při řešení úloh s pruty zatíženými tlakem musíme rozhodnout, který z možných mezních stavů nastane. Uvedeme si příklad pro prut z materiálu v houževnatém stavu.
V běžných konstrukcích nepřipouštíme vznik trvalých deformací ani prohýbání prutů.
Pak musí být splněno:
96
2 a beza) pro λ > λK ⇒ rozhodující je mezní stav vzpěrné stability, Fkr = α2 EJ
l2
pečnost vzhledem k meznímu stavu vzpěrné stability bude kv = FFkr ,
b) pro λ < λK ⇒ rozhodující je mezní stav pružnosti a bezpečnost vzhledem
k meznímu stavu pružnosti bude kK = σσK .
max
97
Příklad 701
16. Matematický popis napjatosti
napjatost
str. 14
na Napjatost v bodě tělesa jsme definovali jako množinu obecných napětí ve všech řezech,
které lze daným bodem tělesa vést. Pro jednoznačný matematický popis napjatosti
stačí znát složky obecných napětí ve třech vzájemně kolmých řezech, které lze vhodným
způsobem sestavit do tenzoru napětí Tσ . Ten lze zapsat ve formě čtvercové matice
σx τxy τxz
Tσ = τyx σy τyz
τzx τzy σz
Vzhledem k symetrii tenzoru napětí, která plyne z předpokladu malých deformací
sdruženost τ na a věty o sdruženosti smykových napětí (τij = τji ) je pouze šest složek tenzoru napětí
str. 14
nezávislých – tři napětí normálová (σx, σy , σz ) a tři smyková (τxy , τxz , τyz ).
16.1. Hlavní souřadnicový systém
hlavní s.s.
str. 38
Významnou vlastností všech tenzorů je existence hlavního souřadnicového sysna tému, v němž jsou mimodiagonální souřadnice tenzoru nulové. Souřadnicové plochy
hlavního souřadnicového systému nazýváme hlavními rovinami. V hlavních rovinách tenzoru napětí nepůsobí tedy smyková napětí (τij = 0), ale jen napětí normálová. Nazýváme je hlavní napětí a zavádíme pro ně značení číslicemi podle konvence
σ1 ≥ σ2 ≥ σ3 .
Tenzor napětí Tσ v hlavním souřadnicovém systému má tvar
σ1 0 0
T σ = 0 σ2 0
0 0 σ3
obecné napětí na
str. 10
Hlavní napětí je normálové napětí v takové rovině, v níž jsou smyková napětí rovna nule
(tj. obecné napětí v řezu je kolmé k tomuto řezu (f~ρ = ~σρ )).
Hlavní napětí σi (i = (1, 2, 3)) lze vypočítat ze známých hodnot tenzoru Tσ v jakémkoliv obecném souřadnicovém systému. Určíme je řešením charakteristické rovnice
tenzoru napětí [1]:
σi3 −I1σi2 +I2σi −I3 = 0,
I 1 = σx + σy + σz ,
kde I1, I2 a I3
jsou invarianty tenzoru napětí dané vztahy
2
2
2
I2 = σx σy + σy σz + σx σz − τxy
− τyz
− τxz
,
98
σx τxy τxz
I3 = τyx σy τyz
τzx τzy σz
16.2. Určení napětí v obecné rovině
Potřebujeme-li ze známých hlavních napětí určit napětí f~ρ , σρ a τρ , je vhodné uvolnit elementární čtyřstěn se třemi stěnami v hlavních rovinách. V hlavních rovinách působí hlavní napětí σ1, σ2 , σ3.
Řez ρ je určen jednotkovým vektorem normály ~eρ ,
který má v hlavním souřadnicovém systému složky
α1, α2 , α3 (αi – směrové kosiny normály roviny ρ).
Při zanedbání objemových sil dostaneme z rovnic
statické rovnováhy elementu vztahy pro složky obecného napětí v řezu ρ
fρ1 = σ1α1 , fρ2 = σ2α2 , fρ3 = σ3 α3
nebo zjednodušeně v maticové podobě
fρ = Tσ · α,
fρ1
σ1 0 0
α1
f
0
σ
0
ρ2 =
· α2
2
α3
fρ3
0 0 σ3
Velikost obecného napětí určíme ze vztahu pro velikost vektoru
fρ =
q
fρ21 + fρ22 + fρ23 =
q
σ12α21 + σ22α22 + σ32α23
Pro posouzení mezních stavů je často důležité znát normálovou (~σρ ) a smykovou (~τρ )
složku obecného napětí f~ρ .
Velikost normálového napětí určíme jako průmět fρ do směru normály k ρ:
σρ = f~ρ · ~eρ = σ1α21 + σ2α22 + σ3 α23
Určit smykové napětí je mnohem složitější, protože neznáme směr jeho působení v rovině ρ. U izotropních materiálů není nutné při vyšetřování mezních stavů znát tento
směr. Proto můžeme určit jen jeho velikost z Pythagorovy věty (viz obr.)
τρ =
q
fρ2 − σρ2,
do níž dosadíme vypočtené hodnoty velikostí fρ a σρ .
16.3. Napětí v oktaedrické rovině
V množině rovinných řezů ρ v bodě tělesa je z hlediska mezního stavu pružnosti významná tzv. oktaedrická rovina, jejíž normála svírá s hlavními osami 1, 2, 3 stejné
úhly α′o , tedy i směrové kosiny αo jsou stejné:
1
α1 = α2 = α3 = αo , α21 + α22 + α23 = 3α2o = 1, ⇒ αo = √
3
Smykové napětí v této rovině je základem podmínky plasticity HMH. Velikost obec- HMH
ného, normálového a smykového napětí v oktaedrické rovině lze určit dosazením směrových kosinů oktaedrické roviny do uvedených vztahů pro napětí v obecném řezu ρ: napětí v řezu ρ
s
na str. 99
1
1 2
fo =
(σ1 + σ22 + σ32 )
σo = (σ1 + σ2 + σ3)
3
3
τo =
q
fo2 − σo2 =
1q
(σ1 − σ2)2 + (σ2 − σ3 )2 + (σ1 − σ3)2
3
99
16.4. Grafické znázornění napjatosti
Další vlastností tenzorů je možnost jejich grafického znázornění v Mohrově rovině, ve
které na vodorovnou osu vynášíme diagonální souřadnice tenzoru (tj. souřadnice na
hlavní diagonále čtvercové matice – v případě tenzoru napětí normálová napětí) a na
svislou osu mimodiagonální souřadnice tenzoru (v případě tenzoru napětí smyková
napětí).
tah na str. 57
krut na str. 72
V kapitole prostý tah jsme takto graficky znázornili jednoosou napjatost a u prostého krutu
napjatost smykovou. Jak ukazuje obrázek, průvodič bodu v Mohrově rovině napjatosti určuje
obecné napětí fρ v daném řezu ρ, dané složkami σρ a τρ . V literatuře [1] je dokázáno:
Při napjatosti v bodě tělesa, určené hlavními napětími σ1, σ2 a σ3 , leží body odpovídající
obecným napětím fρ (ρ je libovolná rovina procházející tímto bodem) ve vyšrafované
oblasti Mohrovy roviny mezi Mohrovými kružnicemi včetně hranice.
napjatost
str. 14
na Vyšrafovaná oblast zahrnující i všechny tři
hraniční kružnice tedy znázorňuje napjatost
v bodě tělesa.
Hlavní napětí σ1 a σ3 jsou extrémní normálová napětí v bodě tělesa, extrémní smyková
napětí jsou
τmax =
σ1 − σ3
= −τmin
2
a působí v řezech, kde je normálové napětí
σ3
σρτmax = σ1 +
2
16.5. Zvláštní typy napjatosti
Zatím jsme se zabývali obecnou napjatostí v bodě tělesa, při níž hlavní napětí jsou
vzájemně různá a nenulová, tj. σ1 6= σ2 6= σ3 6= 0. Často se však setkáváme s případy,
kdy některá hlavní napětí jsou nulová nebo shodná. Mohrovo zobrazení nám dává
rychlou a názornou představu o napjatosti, včetně extrémních hodnot složek napětí.
16.5.1. Trojosá (prostorová) napjatost
1) obecná
σ1 6= σ2 6= σ3 6= 0
2) polorovnoměrná
a) σ1 = σ2 6= 0,
σ3 6= 0
b) σ2 = σ3 6= 0,
σ1 6= 0
100
3) rovnoměrná (hydrostatická)
σ1 = σ2 = σ3 = σ
Při rovnoměrné trojosé napjatosti nepůsobí v žádném řezu smykové napětí. Proto podmínky plasnemůže nastat mezní stav pružnosti, jak plyne z podmínek plasticity, u nichž je vždy ticity na str. 104
rozhodující veličinou nějaké smykové napětí.
16.5.2. Dvojosá (rovinná) napjatost
jedno hlavní napětí je nulové
1) obecná
a) σ3 = 0,
σ1 6= σ2 6= 0
b) σ2 = 0,
σ1 6= σ3 6= 0
c) σ1 = 0, σ2 6= σ3 6= 0
2) rovnoměrná
a) σ3 = 0,
σ1 = σ2 6= 0
b) σ1 = 0,
3) prutová
σ2 = σ3 6= 0
S touto napjatostí se setkáváme u prutů, proto jí
věnujeme podrobnější rozbor. Je dána normálovou
a smykovou složkou napětí v příčném průřezu prutu
předpoklady napjatostní
na
str. 36
σx = σ 6= 0, τxy = τ 6= 0,
přičemž všechna ostatní napětí jsou nulová. Dosadíme do charakteristické rovnice,
abychom určili hlavní napětí, která budeme potřebovat při hodnocení mezních stavů:
σi3 − I1σi2 + I2σi − I3 = 0
2
2
2
I2 = σx σy + σy σz + σxσz − τxy
− τyz
− τxz
= −τ 2
I 1 = σx + σy + σz = σ
σx τxy τxz
I3 = τyx σy τyz
τzx τzy σz
3
2
2
σ τ 0 = τ 0 0 =0
0 0 0 σ −I1 σ +I2 σ −I3 = 0 ⇒ σ(σ −I1σ +I2 ) = 0 ⇒ σI = 0, σII,III
po dosazení za I1 = σ a I2 = −τ 2 dostaneme
σ
σ1 = +
2
s
2
σ
2
+
τ 2,
σ2 = 0,
σ
σ3 = −
2
s
I1
= ±
2
2
σ
2
s
I1
2
2
− I2
+ τ 2.
Protože odmocnina, vyjadřující poloměr největší Mohrovy kružnice, je vždy kladné
číslo, platí σ1 ≥ 0 a σ3 ≤ 0, takže vypočítaná napětí vyhovují relaci σ1 ≥ σ2 ≥ σ3.
101
4) smyková
krut na str. 72
je zvláštním případem prutové napjatosti pro σ = 0. Pak
pro hlavní napětí platí
σ1 = −σ3 = τ,
σ2 = 0.
Tato napjatost se vyskytuje např. u prostého krutu
16.5.3. Jednoosá (přímková) napjatost
dvě hlavní napětí jsou nulová
a) tahová σ1 > 0,
σ2 = σ3 = 0
b) tlaková σ3 < 0,
σ1 = σ2 = 0
16.5.4. Nulová napjatost
σ1 = σ2 = σ3 = 0
102
17. Úvod do nauky o mezních stavech
K čemu je vlastně nauka o mezních stavech? Pro většinu studentů i inženýrů je hlavní,
resp. dokonce téměř jedinou náplní oboru pružnost a pevnost“ určování napětí a defor”
mací, tedy deformačně – napěťová analýza. Vypočítaná napětí se pak už jen porovnají
s nějakou mezní hodnotou, tak proč z toho dělat vědu?
Důvody si ukážeme na příkladu víceosé napjatosti. Jednoduchý postup popsaný výše
totiž dostačuje pouze v případě, že napjatost (pokud je rozhodující veličinou pro vznik
příslušného mezního stavu) je popsána jedinou nenulovou složkou tenzoru napětí. V případě jednoosé tahové napjatosti nebo i napjatosti smykové je posouzení např. mezního tahová napjastavu pružnosti opravdu takto jednoduché; studenti bakalářského studia se navíc s kom- tost na str. 54
plikovanějším typem napjatosti prakticky při výpočtech nesetkali.
smyková napjaPři komplikovanější napjatosti, např. už i napjatosti prutové, charakterizované pouze tost na str. 72
napětími σ a τ v příčném průřezu, není již posouzení mezního stavu vůbec snadné. Pro prutová napjailustraci zkuste zodpovědět zdánlivě banální otázku, který ze zátěžných stavů 1 a 2, tost na str. 99
daných tenzory napětí Tσ1 a Tσ2 v nebezpečném bodě tělesa je nebezpečnější, tj. ve
kterém je větší riziko ztráty provozuschopnosti (funkčnosti) součásti:
Tσ1
50 50 0
= 50 0 0
0 0 0
Tσ2
70 40 0
= 40 0 0
0 0 0
Odpověď dokonce není jednoznačná, ale závisí na tom, zda chování materiálu bude
křehké nebo houževnaté. U křehkého materiálu má větší vliv normálové napětí, které
je vyšší u napjatosti Tσ2 , zatímco u houževnatého materiálu bude významnější vliv
smykového napětí, které je vyšší u napjatosti Tσ1 . Ještě komplikovanější bude situace
při posuzování obecné napjatosti, dané šesti nezávislými číselnými hodnotami, z nichž napjatost
některé při přechodu do jiného zatěžovacího stavu rostou, jiné klesají nebo zůstávají str. 14
beze změny. Posuzujete-li např. zavěšení pravého předního kola automobilu, je nebezpečnější prudké brždění, ostrý průjezd levotočivou zatáčkou nebo přejezd výmolu ve
vozovce? Ve všech případech bude zatížení závěsu kola zcela odlišné. Ani odpověď
na otázku, za jakých podmínek nazveme přechod z jednoho do druhého zatěžovacího
stavu zatěžováním, resp. odlehčováním, není jednoduchá. Zkuste jen rozhodnout, zda
přechod ze zátěžného stavu, charakterizovaného v nebezpečném bodě uvedeným tenzorem napětí Tσ1 , do stavu Tσ2 je zatěžováním nebo odlehčováním. Obecná odpověď se
dá formulovat následovně:
Proces změny napěťově deformačních parametrů tělesa nazveme zatěžováním, jestliže
v konečném stavu existuje vyšší riziko vzniku nějakého mezního stavu než ve stavu
výchozím. Opačný proces nazveme odlehčováním tělesa.
Je tedy zřejmé, že je třeba najít způsob, jak hodnotit riziko vzniku mezních stavů
v případě, že o něm rozhoduje veličina popsaná více než jedním číselným parametrem
(tedy např. tenzorová). A právě tento problém řeší nauka o mezních stavech.
17.1. Součinitel bezpečnosti
Schopnost soustavy plnit požadované funkce za běžných i některých mimořádných podmínek (např. tlaková zkouška) označujeme jako spolehlivost soustavy. Spolehlivost
103
na
musíme nějak kvantifikovat, posoudit, jak podstatně se smí změnit veličiny ovlivňující
mezní stav, aniž by došlo ke ztrátě provozuschopnosti. Protože každá z výpočtových veličin má stochastický charakter, nemůžeme za provozu připustit stavy blízké meznímu
stavu, ale musí vůči jeho dosažení existovat určitá rezerva – bezpečnost. K jejímu posouzení potřebujeme najít fyzikální veličinu α, jednoznačně popisující vznik mezního
stavu (např. napětí normálové, smykové, redukované, deformační parametr, zátěžná
síla, počet zátěžných cyklů, aj.). Pro tuto veličinu je pak součinitel bezpečnosti, zkráceně bezpečnost (přesněji pro odlišení nazývaná prostá bezpečnost) vůči příslušnému
meznímu stavu dána vztahem
M
k=α
αP ,
kde αM je mezní hodnota a αP je provozní hodnota příslušné veličiny.
V praxi musí být k > 1. Pokud k = 1, nastává příslušný mezní stav. Jeho konkretizací
můžeme definovat např.
( meznímu stavu deformace
kD = uumezní
max
K
meznímu stavu pružnosti
kK = σσmax
bezpečnost vůči
σ
Rt
meznímu stavu křehké pevnosti
kR = σmax
jednoosá napja- Uvedené vztahy však platí pouze tehdy, když je vznik mezního stavu jednoznačně
tost na str. 99
popsán příslušnou číselnou hodnotou (tj. např. u jednoosé tahové napjatosti).
17.2. Mezní stav pružnosti
prut na str. 36
tah na str. 53
krut na str. 71
ohyb na str. 78
Doposud jsme se zabývali modelovým tělesem – prutem, který byl namáhán prostým
tahem, krutem nebo ohybem. U prostého tahu a ohybu vznikla v prutu jednoosá napjatost, u prostého krutu napjatost smyková. Řešili jsme napjatost a deformaci pro
tato namáhání a při řešení úloh jsme se setkali s mezními stavy pružnosti a deformace.
Bezpečnost vzhledem k meznímu stavu pružnosti jsme určovali podle vztahů
pro tah a ohyb kK =
kombinované
namáhání
na
str. 41
prutová napjatost na str. 99
σK
,
σmax
pro krut kK =
τK
σK
=
.
τmax
2τmax
Kombinované namáhání prutů vyžaduje popis mezních stavů při prutové napjatosti,
jiné modely (analytické či numerické) dávají ještě složitější typy napjatostí v nebezpečných bodech. Nejjednodušší úroveň popisu mezního stavu pružnosti při obecné napjatosti vyžaduje:
– monotonně rostoucí zatěžování (podmínka plasticity neplatí pro cyklické zatěžování),
– izotropní materiál z hlediska mezního stavu pružnosti (podmínka plasticity nezávisí na směru působení napětí),
– jednoparametrický mezní stav pružnosti (mezní stav pružnosti je popsán jedinou
materiálovou charakteristikou – mezí kluzu σK , stejnou pro tah i tlak).
Chceme-li posuzovat vznik mezního stavu pružnosti, musíme zformulovat podmínku
plasticity, což je matematické vyjádření mezního stavu pružnosti a znát mezní hodnotu, která ho popisuje (mez kluzu – materiálová charakteristika). Jako podmínku
plasticity při jednoosé napjatosti označujeme vztah σ = σK , který lze vyjádřit
obecně ve tvaru
F (σ) = σK ,
kde F je funkce v daném případě jediné proměnné σ.
104
Podmínka plasticity pro trojosou napjatost musí být dána funkcí tenzoru napětí,
tedy šesti proměnných
F (Tσ ) = F (σx, σy , σz , τxy , τyz , τxz ) = σK .
Pro grafické znázornění podmínek plasticity se
zavádí Haighův prostor, jehož souřadnicové
osy jsou osami hlavních napětí. V tomto prostoru je podmínka plasticity znázorněna plochou plasticity, zatěžování je znázorněno křivkou – zatěžovací dráhou. Mezní stav pružnosti
při zatěžování nastane, až zatěžovací cesta protne plochu plasticity.
Z rozsáhlých experimentů vyplynul závěr, že mezní stav pružnosti je určen velikostí
smykového napětí |τρK | v jistém řezu ρK a podmínka plasticity má tvar
F (|τρK |) = MK
(MK je materiálová charakteristika).
Nejjednodušší, prakticky použitelnou funkcí F (vyjadřující podmínku plasticity), je
funkce lineární a odpovídající podmínka plasticity má tvar
F (|τρK |) = |τρK | = τM K ,
kde τM K je materiálová konstanta.
Řez ρK byl volen na základě zkušeností z experimentů a podle volby řezu dostaneme
různé podmínky plasticity.
17.2.1. Podmínka plasticity max τ (Trescova)
Podmínka plasticity maximálních smykových napětí předpokládá, že řezem ρK je řez,
ve kterém působí maximální smykové napětí τmax a může být proto vyjádřena ve tvaru
τmax = τM K
Mezní stav pružnosti při monotónním zatěžování materiálu v základním strukturním
stavu z nezatíženého stavu nastane, když maximální smykové napětí dosáhne mezní
hodnoty τM K , která je materiálovou charakteristikou.
Pro obecnou napjatost:
τmax =
σ1 − σ3
= τM K
2
Pro jednoosou napjatost:
σ1
σK
=
= τM K ,
2
2
protože σ2 = σ3 = 0 a v mezním stavu pružnosti je σ1 = σK .
τmax =
Cílem je posoudit možnost vzniku mezního stavu při víceosé napjatosti pomocí experimentů prováděných pouze při napjatosti jednoosé (tahová zkouška), proto porovnáme
obě napjatosti a dostaneme:
τM K =
σ1 − σ3
σK
=
2
2
⇒
105
σ1 − σ3 = σK
Zavedeme-li redukované napětí
σred = σ1 − σ3 ,
dostaneme tvar analogický napjatosti jednoosé σred = σK
určíme ze vztahu
K .
kK = σσred
prostá
bezpečnost
a součinitel bezpečnosti
Redukované napětí σred
je fiktivní hodnota jednoosého tahového napětí, přiřazená dané víceosé napjatosti, která
má stejnou prostou bezpečnost vůči vyšetřovanému meznímu stavu jako tato víceosá
napjatost.
Posouzení mezního stavu pružnosti pomocí redukovaného napětí je pak již stejné jako
u jednoosé napjatosti.
σred < σK
σred = σK
σred > σK
– materiál v elastickém stavu,
– dosažení mezního stavu pružnosti,
– materiál je ve vyšetřovaném bodě ve stavu plastickém.
Uvedený obecný tvar podmínky plasticity max τ platí pro jakoukoli napjatost, musíme
hlavní napětí na však pro ni umět určit všechna 3 hlavní napětí. Pro konkrétní typy napjatosti (jednoosá
str. 98
napjatost při tahu, tlaku a ohybu prutů, dvouosá smyková napjatost při krutu a prutová
napjatost při kombinovaném namáhání prutů) je možné podmínku plasticity max τ ,
tah na str. 54
ohyb na str. 79 resp. vztah pro redukované napětí zjednodušit do následujících tvarů:
krut na str. 72
1) Jednoosá (přímková) napjatost
jednoosá napja- a) tahová
tost na str. 99
σ1 = σ > 0, σ2 = σ3 = 0 ⇒ σ = σK
b) tlaková
σ3 = σ < 0,
σ1 = σ2 = 0 ⇒ | σ| = σK
smyková napja- 2) Smyková napjatost
tost na str. 99
σ1 = −σ3 = τ
σred = | σ|
σ2 = 0
σ1 − σ3 = τ − (−τ ) = σK ⇒ 2τ = σK
σred = 2τ
v mezním stavu pružnosti τ = τK ⇒ τK = σ2K (τK . . . mez kluzu ve smyku)
prutová napja- 3) Prutová napjatost
tost na str. 99
s
s
2
2
σ
σ
σ
σ
σ1 = +
+ τ 2 σ2 = 0 σ3 = −
+ τ2
2
2
2
2
Po dosazení do podmínky plasticity dostaneme
σ1 − σ3 = σ2 +
r 2
σ
2
+
τ2
− σ2 +
r 2
σ
2
+ τ2 =
106
√
σ 2 + 4τ 2 = σK σred =
√
σ 2 + 4τ 2
17.2.2. Podmínka plasticity HMH (Misesova)
Podmínka plasticity HMH (podle jmen autorů této podmínky – Hencky, Mises, Huber)
předpokládá, že řezem ρK je oktaedrická rovina a může být proto vyjádřena ve tvaru oktaedrická ro|τo | = τoK
vina na str. 98
Mezní stav pružnosti při monotónním zatěžování materiálu v základním strukturním
stavu z nezatíženého stavu nastane, když smykové napětí v oktaedrické rovině dosáhne
mezní hodnoty τoK , která je materiálovou charakteristikou.
Pro smykové napětí v oktaedrické rovině platí pro obecnou napjatost:
1q
(σ1 − σ2 )2 + (σ2 − σ3)2 + (σ1 − σ3)2 .
3
τo =
τo na str. 98
Pro tahovou napjatost (σ1 = σK , σ2 = σ3 = 0) je:
√ q
√
2
2
2
σK .
τo =
σK
= τoK ⇒ τoK =
3
3
Cílem podmínek plasticity je porovnání obecné napjatosti, pro niž nelze provádět materiálové zkoušky, s napjatostí jednoosou, realizovanou na zkušebním stroji pro zkoušky
tahem, při níž zjišťujeme mj. mez kluzu. U podmínky HMH je kriteriem pro porovnání
různých typů napjatostí smykové napětí v oktaedrické rovině τo . Porovnáním hodnot
smykových napětí v oktaedrické rovině u obecné a jednoosé napjatosti dostaneme
√
1q
2
(σ1 − σ2 )2 + (σ2 − σ3)2 + (σ1 − σ3 )2 =
σK
3
3
Podmínka plasticity HMH pro obecnou napjatost určenou hlavními napětími σ1, σ2, σ3 :
s
i
1h
(σ1 − σ2 )2 + (σ2 − σ3)2 + (σ1 − σ3 )2 = σK
2
Zavedeme-li
σred =
r
i
zde
h
redukované
napětí
i
1 (σ − σ )2 + (σ − σ )2 + (σ − σ )2 ,
1
2
2
3
1
3
2
pak se podmínka zjednoduší do tvaru σred = σK a součinitel bezpečnosti určíme ze
K .
vztahu
kK = σσred
Významnou výhodou podmínky plasticity HMH je, že vztah pro redukované napětí lze
odvodit přímo pro složky napětí v obecném souřadnicovém systému, a to ve tvaru
σred =
s
i
1h
2 + τ2 + τ2
(σx − σy )2 + (σy − σz )2 + (σx − σz )2 + 6 τxy
yz
xz
2
1) Jednoosá (přímková) napjatost
a) tahová
σ1 = σ > 0,
s
jednoosá napjatost na str. 99
σ2 = σ3 = 0 ⇒
1 2
(σ + σ 2) = σK ⇒
2
σ = σK
107
b) tlaková
σ3 = σ < 0,
smyková napja- 2) Smyková napjatost
tost na str. 99
σ1 = −σ3 = τ
σred =
s
σ1 = σ2 = 0 ⇒ | σ| = σK
σred = | σ|
σ2 = 0
1 2
[τ + τ 2 + (2τ )2 ] = σK
2
⇒
√
3τ = σK
σK
v mezním stavu pružnosti τ = τK ⇒ τK = √
3
σred =
√
3τ
(τK . . . mez kluzu ve smyku podle HMH)
prutová napja- 3) Prutová napjatost
tost na str. 99
σx = σ 6= 0; τxy = τ 6= 0; σy = σz = 0; τxz = τyz = 0.
Do vztahu pro redukované napětí v obecném souřadnicovém systému lze tyto hodnoty přímo dosadit,
tím dostaneme
s
i
1h
2 + τ2 + τ2
(σx − σy )2 + (σy − σz )2 + (σx − σz )2 + 6 τxy
yz
xz
2
√
Podmínka plasticity HMH pro prutovou napjatost:
σK = σ 2 + 3τ 2
√
a redukované napětí
σred = σ 2 + 3τ 2
σred =
Z hlediska praktického použití jsou obě uvedené podmínky plasticity rovnocenné. Při
ručních výpočtech se často používá podmínka max τ , protože její tvar je jednodušší.
hlavní napětí na Její nevýhodou však je, že u ní musíme určit velikosti hlavních napětí a jejich pořadí
str. 98
podle velikosti, protože se v ní nevyskytuje jedno hlavní napětí (σ2 ). Podmínka HMH je
sice pro výpočet složitější, ale při řešení na počítači to nevadí, a tak se v počítačových
programech z uvedeného důvodu používá častěji. Navíc byla odvozena i pro obecný
souřadnicový systém, takže nevyžaduje znalost hlavních napětí.
17.3. Obecná a prostá bezpečnost
Pro usnadněné vyjádření bezpečnosti vůči meznímu stavu pružnosti jsme zavedli koeficient bezpečnosti jako
σK
kk =
.
σred
Změna jednotlivých složek tenzoru napětí se však do změny bezpečnosti promítne různým způsobem, takže pomocí redukovaného napětí lze bezpečnost správně určit jedině tehdy, pokud nárůst všech složek napětí při zatěžování a přetěžování je vzájemně
přímo úměrný. Takový způsob zatěžování a přetěžování je graficky (např. v Haighově
Haighův prostor prostoru) znázorněn přímkou a nazýváme jej prostým zatěžováním a přetěžováním.
na str. 104
Koeficient bezpečnosti pro prosté zatěžování se nazývá prostá bezpečnost a je možno
jej určit pomocí redukovaného napětí. Není-li zatěžování a přetěžování prosté (např. nárůst kroutícího momentu v hřídeli není úměrný nárůstu ohybového momentu, proto
108
složky napětí σ a τ nejsou vzájemně úměrné), pak nelze použít redukované napětí.
V tom případě se určuje tzv. obecná bezpečnost, která respektuje způsob zatěžování i přetěžování.
109
18. Metoda konečných prvků
Mezi moderními metodami napěťově-deformační analýzy dnes jednoznačně dominuje
metoda konečných prvků (dále jen MKP), používaná i v jiných oblastech inženýrských
výpočtů (vedení tepla, proudění kapalin, elektřina a magnetismus). V oblasti mechaniky těles MKP umožňuje řešit tyto základní typy úloh:
– napěťově deformační analýza při statickém, cyklickém i dynamickém zatěžování,
včetně nejrůznějších nelineárních úloh;
– vlastní i vynucené kmitání soustav s tlumením i bez tlumení;
– kontaktní úloha pružnosti (rozložení stykového tlaku);
– stabilitní problémy (ztráta tvarové stability konstrukcí);
– analýza stacionárního i nestacionárního vedení tepla a určení teplotní napjatosti
(včetně zbytkové).
MKP je založena na zcela jiném principu než analytické metody pružnosti. Zatímco
analytické metody jsou založeny na diferenciálním a integrálním počtu, MKP je založena na obecně méně známém počtu variačním, hledá minimum nějakého funkcionálu.
Poznámka:
Funkce - zobrazení mezi množinami čísel. Je to tedy matematický termín pro pravidlo,
kterým jednoznačně přiřadíme nějaké číselné hodnotě (z definičního oboru funkce) jinou
číselnou hodnotu (z oboru funkčních hodnot).
Funkcionál - zobrazení z množiny funkcí do množiny čísel. Je to tedy pravidlo, podle
něhož přiřadíme funkci na jejím definičním oboru (nebo jeho části) nějakou číselnou
hodnotu. Příkladem je určitý integrál funkce.
Základním funkcionálem v deformačně – napěťové analýze pružných těles je jejich
energie napjatosti. Je to práce spotřebovaná na deformaci tělesa, která je v případě pružné deformace vratná, tj. dá se z tělesa při návratu do původního nedeformovaného tvaru zpětně získat (pružiny). V souladu s definicí funkcionálu je to číselná
hodnota, přiřazená funkcím popisujícím deformační posuvy jednotlivých bodů tělesa
(jsou-li posuvy základními neznámými funkcemi, jedná se o nejběžnější, tzv. deformační variantu MKP). Pro libovolný deformovaný tvar tělesa je možné tuto energii
napjatosti určit z přetvoření a napětí ve všech bodech tělesa. Při daném zatížení a vazbách k okolí nemůže v praxi těleso zaujmout libovolný tvar, nýbrž jeho deformovaný
tvar je jednoznačně definován (s výjimkou některých stabilitních problémů). Z různých
možných deformovaných tvarů tělesa je to ten energeticky nejméně náročný, což matematicky vyjadřuje tzv. věta o minimu kvadratického funkcionálu. Formuluje
obecný přírodní princip, že z možných dějů proběhne ve skutečnosti vždy ten, k jehož uskutečnění je zapotřebí minimální energie (např. ostří nože nebo sekery projde
materiálem vždy cestou nejmenšího odporu). Z možných deformovaných tvarů tělesa,
odpovídajících definovaným okrajovým podmínkám (zatížení, vazby), se proto realizuje ten, jenž je energeticky nejméně náročný. Příslušným energetickým funkcionálem,
jehož minimum určí skutečný deformovaný tvar tělesa, je celková potenciální energie tělesa Π, definovaná jako rozdíl energie napjatosti tělesa W a potenciální energie
vnějšího zatížení P .
Π=W −P
Celková potenciální energie tělesa je samozřejmě funkcí posuvů jeho jednotlivých bodů.
Variační metody matematiky pak umožňují najít minimum funkcionálu, tedy nalézt
110
takový tvar, v němž bude při daných okrajových podmínkách (zatížení, vazby) funkcionál Π nejmenší, a který se proto ve skutečnosti jako jediný realizuje.
Z deformačních posuvů jednotlivých bodů v tomto stavu tělesa pak je možno určit
složky tenzoru přetvoření a z nich pomocí konstitutivních vztahů (při známých materi- tenzor přetvoálových charakteristikách) následně složky tenzoru napětí. Prakticky výpočet probíhá ření na str. 18
tak, že za pomoci počítačového programu pro přípravu vstupních dat (preprocesingu)
se vytvoří geometrický model tělesa nebo soustavy, který se spojitě, tj. beze zbytku,
rozdělí na prvky konečných rozměrů. Základním prvkem v rovině je čtyřúhelník, v prostoru pak šestistěn (anglicky brick = kostka, cihla), někdy je nutné použít zjednodušené
tvary prvku (trojúhelník, čtyřstěn).
Rohy těchto prvků, případně některé další význačné body, jsou uzlovými body, v nichž
se určují neznámé hodnoty posuvů, strany (hrany) prvků vytvářejí síť, jejíž hustota je
rozhodující pro přesnost výsledků. Hrany prvků jsou obvykle přímé, ale pomocí kvadratických prvků lze realizovat i zakřivené. Kvadratické prvky mají kromě rohových
uzlů ještě další uzly uprostřed stran (resp. hran), čímž dostáváme v rovině prvek osmiuzlový a v prostoru prvek (brick) dvacetiuzlový. Tyto prvky mnohem lépe vystihují
lokální koncentraci napětí při použití hrubé sítě (viz následující příklad).
Vpravo je barevně znázorněno rozložení největšího hlavního napětí v symetrické polovině osazeného prutu, červená barva odpovídá nejvyšší hodnotě napětí (kořen vrubu).
Napětí ve směru podélné osy hřídele má ve vrubu nominální hodnotu 1 MPa, maximální
1,676 MPa. Z následující tabulky je zřejmé, že v případě jemné sítě dávají oba typy
prvků správné výsledky, pro hrubou síť je při použití lineárních prvků chyba mnohem
větší, než při použití prvků kvadratických.
111
Typ prvku
Hustota sítě vypočtené max. napětí [MPa]
lineární - čtyřuzlový
hrubá
1,28
lineární - čtyřuzlový
jemná
1,67
kvadratický - osmiuzlový
hrubá
1,59
kvadratický - osmiuzlový
jemná
1,67
Tabulka uvádí hodnoty maximálního napětí v kořeni vrubu (osazení hřídele) při tahovém namáhání, vypočtené s různými typy prvků pro hrubou a jemnou síť podle
obrázku.
Bodů, ve kterých určujeme posuvy, nemůže být v praxi samozřejmě nekonečně mnoho.
Hustotu sítě těchto bodů volí výpočtář na základě své zkušenosti. V případě příliš
husté sítě trvá řešení příliš dlouho, naopak příliš řídká síť může vést k podhodnocení
napětí, jestliže u něj existuje výrazný lokální extrém (např. vrub, viz předchozí příklad).
Současné programy zvládají více nebo méně kvalitně automatickou tvorbu sítě, ale
téměř vždy tato síť klade výrazně vyšší nároky na výpočtový čas a paměť počítače,
než když ji vytváří zkušený výpočtář. U trojrozměrné úlohy představuje každý uzlový
bod sítě tři neznámé parametry, a to hodnoty jeho posuvů ve třech směrech. Současné
počítače řeší běžně v rozumných výpočtových časech úlohy o desetitisících až statisících
neznámých parametrech.
Kontrolní
otázka
Všem prvkům je třeba zadat konstitutivní parametry materiálu (pro izotropní lineárně
elastický materiál jsou to modul pružnosti a Poissonovo číslo). Dále se definují okrajové
podmínky (vazby, zatížení), které pro statickou úlohu musí zajistit jednoznačnou polohu tělesa v prostoru (případné omezení deformace – statická neurčitost – úlohu nijak
nekomplikuje, předepíše se jen více okrajových podmínek). Následuje spuštění řešiče
(solveru), což je program, který na základě vstupních hodnot sestaví a vyřeší soustavu
rovnic s neznámými posuvy a z nich spočítá přetvoření a napětí. Bez zadání všech
vstupních údajů nelze řešič spustit, takže metodou konečných prvků není možné řešit nepřímé úlohy, tj. úlohy, které mají neznámé parametry geometrie, zatížení apod.
Poslední částí programového systému je postprocesing, neboli program pro zpracování
výsledků. Umožňuje v nejrůznějších podobách znázornit rozložení kterýchkoli výstupních parametrů (např. složek napětí, posuvů aj.) v tělese nebo zvolené podoblasti, stejně
jako počítat redukovaná napětí nebo jiné hodnoty potřebné pro posuzování mezních
stavů.
112
19. Nomogramy součinitelů koncentrace napětí
Vztahy prosté pružnosti prutů lze použít pouze pro tělesa s nepodstatnými odchylkami
od prutových předpokladů. Protože většina konstrukcí obsahuje součásti s náhlou změnou příčného průřezu, která je buď vytvořena účelově (drážky, zápichy, otvory, osazení),
nebo představuje vadu (trhliny), je třeba oblast takové změny průřezu posoudit z hlediska možnosti dosažení některého z mezních stavů. Právě v těchto místech totiž vzniká
většina provozních lomů.
Přítomnost vrubů má za důsledek přerozdělení průběhu napětí v průřezu, vruby způsobují
místní koncentraci přetvoření a tím i koncentraci napětí (v blízkém okolí vrubu neodpovídá
rozložení napětí teorii prostého namáhání prutu
a vzniká zde obecná trojosá napjatost). Velikost koncentrace napětí se zjednodušeně určuje
pomocí součinitele koncentrace napětí α,
který je definován vztahy
α=
σex
σn
(pro namáhání tahem a ohybem) a α =
τex
τn
prutové předpoklady na str. 36
mezní stav na
str. 5
vruby na str. 59
trojosá napjatost na str. 99
(pro namáhání krutem).
Nominální napětí σn a τn jsou napětí určená podle vztahů pro prosté namáhání tahem, tah na str. 54
ohybem a krutem.
ohyb na str. 79
Hodnoty součinitelů koncentrace napětí α stanovené numerickými (MKP) nebo expe- krut na str. 73
rimentálními (fotoelasticimetrie) metodami pro různé tvary vrubů a různé způsoby
namáhání, jsou zpracovány do grafů [7]. V úvodních schématech, v nichž jsou znázorněny odpovídající tvary vrubů, je uveden rovněž vztah pro nominální napětí σn ,
k němuž se vztahuje součinitel α.
Kruhová tyč se zápichem namáhaná
tahem
ohybem
krutem
σn = 4F2
πd
σn = 32M3 o
πd
τn = 16M3k
πd
graf na str. 114
graf na str. 115
graf na str. 115
tahem
Kruhová tyč s osazením namáhaná
ohybem
krutem
σn = 4F2
πd
σn = 32M3 o
πd
τn = 16M3k
πd
graf na str. 116
graf na str. 116
graf na str. 117
113
Plochý prut se zápichem namáhaný
tahem
ohybem
σn = F
bs
o
σn = 6M
b2 s
graf na str. 117
graf na str. 118
Plochý prut s osazením namáhaný
tahem
ohybem
Lomený prut namáhaný
ohybem
F
σn = bs
o
σn = 6M
b2 s
σn = 6M2o
bh
graf na str. 118
graf na str. 119
graf na str. 119
Přehled tvarů na str. 113
114
Přehled tvarů na str. 113
Přehled tvarů na str. 113
115
Přehled tvarů na str. 113
Přehled tvarů na str. 113
116
Přehled tvarů na str. 113
Přehled tvarů na str. 114
117
Přehled tvarů na str. 114
Přehled tvarů na str. 114
118
Přehled tvarů na str. 114
Přehled tvarů na str. 114
119
s01. Základy statiky nutné pro PP
Poznámka:
Tato stať není přehledem statiky, ale pouze připomenutím některých základních poznatků, bez nichž se v PP nelze obejít.
s01.1. Mechanický pohyb
Pohyb chápeme obecně jako změnu polohy jakéhokoli reálného (např. člověk) nebo
abstraktního (např. informace, myšlenka) objektu v čase. Mechanický pohyb pak
je pouze pohyb hmotných objektů. Mechanika těles se zabývá jen pohybem těles,
čili hmotných objektů tvořených látkou v tuhém skupenství. Tento pohyb lze rozčlenit
následovně:
1. pohyb tělesa jako celku – změna polohy bodů tělesa vzhledem k souřadnicovému systému spojenému se základním tělesem (obvykle se Zemí), ale beze změny
vzdálenosti libovolných 2 bodů či úhlu libovolných 3 bodů tělesa.
deformace tělesa
na str. 18
2. deformace – změna vzdálenosti
2 bodů resp. úhlu 3 bodů tělesa, bez
změny spojitosti.
3. porušení spojitosti – vznik nebo šíření trhliny v tělese.
Je definováno tak, že existují 2 body A, B tělesa T takové,
že v čase t1 jsou všechny body spojnice AB prvky tělesa T
a v čase t2 existuje bod spojnice A’B’, který není prvkem
tělesa T.
lom na str. 7
4. oddělení části tělesa – rozpad tělesa na 2 nebo více částí, které se mohou pohybovat nezávisle na sobě (např. výbuch šrapnelu).
s01.2. Silové působení a síla působící na těleso
zatížení silové na Podle charakteru oblasti, která je z hlediska silového působení významná, rozlišustr. 21
jeme:
120
a) objemové silové působení
významnou oblastí je prostorová oblast. Tento charakter
mají silová pole gravitační, elektromagnetická, setrvačná. . ..
Je určeno oblastí Ω, ve které působí rozložené měrné objemové síly ~o(x, y, z) [N/m3]
b) plošné silové působení
významnou oblastí je plošná oblast. Tento charakter má silové
působení mezi tělesy prostřednictvím stykových vazeb nebo tlak
tekutého média na těleso. Je určeno stykovou oblastí Γ a měrnou plošnou silou p~(x, y, z) [N/m2]
Za určitých okolností lze tato silová působení popsat pomocí následujících modelů:
– liniová síla
významná oblast má dominantní 1 rozměr, ostatní jsou z hlediska řešeného problému nepodstatné. Je určeno prostorovou
křivkou γ a měrnou liniovou silou ~q(x, y, z) [N/m]
– osamělá síla
rozměry stykového útvaru jsou z hlediska řešeného problému
nepodstatné.
s01.3. Axiomy o silovém působení
a) Silové působení v δ okolí bodu A, které je z hlediska řešeného problému nepodstatné, je vektorová veličina – síla F~ vázaná k bodu A.
b) Působení síly F~ v bodě A tělesa
lze z hlediska pohybové ekvivalence
(tj. z hlediska ovlivnění pohybu tělesa jako celku) vyjádřit v libovolném
bodě B silou~F~ a momentem
~ × F~ .
MB = BA
n
o
c) Působení soustavy Π1 = Ai, F~i na těleso T je pohybově ekvivalentní s působením
n
o
soustavy Π2 = Aj , F~j , jestliže platí
n
X
i=1
F~i =
m
X
j=1
F~j
^
121
n
X
i=1
~ Bi =
M
m
X
j=1
~ Bj
M
s01.4. Moment síly k bodu
Moment síly F~ s působištěm v bodě A k počátku 0
souřadnicové soustavy:
~ 0 = 0A
~ × F~ = ~rA × F~
M
~i ~j ~k
~ 0 = xA yA z A
M
Fx Fy Fz
[Nm]
= (yA Fz − zA Fy )~i + (zA Fx − xA Fz )~j + (xA Fy − yA Fx)~k
= Mx~i + My~j + Mz ~k
Je to vektor vázaný k bodu 0 a kolmý k rovině (~rA , F~ ). Jeho velikost
M0 = F rA sin ϕ = F d, d = rA sin ϕ
~ 0 v uvedeném pořadí tvořily pravotočivou soua smysl je takový, aby vektory ~rA , F~ , M
stavu (pravidlo pravé ruky, pravotočivý šroub).
s01.5. Moment síly k ose p
~ p síly F~ působící v bodě A k ose p je průmět vektoru
Moment M
momentu síly k libovolnému body osy p do směru osy p.
~p = M
~ B · ~ep · ~ep =
M
h
i
~ × F~ · ~ep · ~ep ,
BA
kde ~ep = cos αp~i + cos βp~j + cos γp~k je jednotkový vektor osy p
a B je libovolný bod na ose p.
~p =
M
h
r~A × F~ · ~ep
i
cos αp
cos βp
cos γp
· ~ep = xA − xB yA − yB zA − zB
Fx
Fy
Fz
s01.6. Podmínky statické ekvivalence
·~
e
p
Silové soustavy Π1 a Π2 působící na těleso T jsou staticky ekvivalentní, jestliže platí
^
(1)
(2)
~ (1) = M
~ (2) ,
F~ = F~
M
V
V
VB
VB
kde B je libovolný, konkrétní, pro obě soustavy shodný bod.
Podmínku statické ekvivalence můžeme vyjádřit
P
(1)
P
P
(2)
Fix = Fjx
P (1)
P (2)
Fiy = Fjy
P (1)
P (2)
Fiz = Fjz
algebraicky
(ve složkovém tvaru)
3 silové podmínky SE
vektorově
P
P (2)
(1)
F~i = F~j
V
122
(1)
P
(2)
MixB = MjxB
P (1)
P (2)
MiyB = MjyB
P (1)
P (2)
MizB = MjzB
3 momentové podmínky SE
P
~ (1) = P M
~ (2)
M
iB
jB
s01.7. Podmínky statické rovnováhy
Těleso je ve statické rovnováze tehdy, je-li jeho zrychlení nulové. Ze silového hlediska to znamená, že jak součet sil, působících na těleso, tak součet jejich momentů
k libovolnému (ale stejnému) bodu je roven nule:
vektorově
algebraicky
P
P
P (2)
(1)
F~i + F~j = ~0
(1)
P
(2)
Fix + Fjx = 0
P (1) P (2)
Fiy + Fjy = 0
P (1) P (2)
Fiz + Fjz = 0
V
P
~ (1) + P M
~ (2) = ~0
M
iB
jB
P
(1)
P
(2)
MixB + MjxB = 0
P (1)
P (2)
MiyB + MjyB = 0
P (1)
P (2)
MizB + MjzB = 0
Algebraicky jsou dvě vektorové statické podmínky (rovnováhy nebo ekvivalence)
vyjádřeny šesti rovnicemi. Jsou to 3 podmínky silové a 3 momentové. Jsou-li vztaženy
k počátku globálního souřadnicového systému, mluvíme o podmínce v základním globální s.s.
tvaru.
Triviální statické podmínky jsou identicky splněny v důsledku prostorového rozložení silové soustavy Π (~0 = ~0).
Lineárně závislou nazýváme takovou statickou podmínku, která je lineární kombinací
ostatních podmínek.
Pužitelné statické podmínky jsou právě všechny nezávislé a netriviální statické
podmínky. Platí pro ně ν ≤ 6.
počet použitelných statických podmínek označujeme ν = νF + νM
počet použitelných statických podmínek silových νF
momentových νM
s01.8. Použitelné statické podmínky pro různé silové soustavy
a) Obecná prostorová silová soustava
ν = 6,
νF = 3,
b) Centrální prostorová soustava sil
ν = 3, νF = 3, νM = 0
c) Soustava sil na společné nositelce
ν = 1, νF = 1, νM = 0
123
νM = 3
d) Centrální rovinná silová soustava
ν = 2, νF = 2, νM = 0
e) Obecná rovinná silová soustava
ν = 3, νF = 2, νM = 1
f) Soustava rovnoběžných sil v prostoru
ν = 3, νF = 1, νM = 2
g) Soustava sil v rovnoběžných rovinách
ν = 5, νF = 2, νM = 3
h) Prostorová soustava sil, které protínají jednu
přímku
ν = 5, νF = 3, νM = 2
124
i) Soustava silových dvojic
v rovnoběžných rovinách
ν = 1, νF = 0, νM = 1
s01.9. Těžiště
– Tíhová síla je staticky ekvivalentní náhrada soustavy elementárních tíhových sil.
– Těžiště je bod, kterým prochází nositelka tíhové síly (osa soustavy elementárních
tíhových sil) při každém natočení tělesa.
– Tíhová síla má vzhledem k souřadnicovému systému spojenému se Zemí stejnou
velikost, směr a smysl při každém natočení tělesa.
– Poloha těžiště v souřadnicovém systému (0, x, y, z) je jednoznačně určena vztahy
xT =
R
Ω
xdFG
FG
=
R
xdm
Ω
m
,
yT =
R
Ω
ydFG
FG
=
R
ydm
Ω
zT =
,
m
R
Ω
zdFG
FG
Tyto vztahy můžeme pro konkrétní případy zjednodušit.
1. Homogenní těleso (dm = ρdV, ρ =konst): xT =
R
ΩR
ΩR
γ
z dS
ydV
ΩR
dV
,
zT =
ΓR
dS
yT =
,
R
,
zT =
,
zT =
ydS
ΓR
dS
Γ
.
dS
xT =
R
γR
γ
z dl
dl
xdS
Γ
3. Tělesa typu prut (dV = Sdl, S =konst):
γR
yT =
,
.
m
Ω
R
Γ
R
dV
R
zdm
Ω
.
dV
2. Tělesa tvaru desek (dV = tdS, t =konst): xT =
ΓR
xdV
Ω
z dV
Ω
R
R
=
R
xdl
dl
,
yT =
R
γR
γ
ydl
dl
.
4. Složené těleso:
Oblast Ω, kterou těleso zaujímá, rozdělíme na konečný počet (n) podoblastí.
125
R
xdm
Ω
xT = R
dm
=
R
xdm +
Ω1
R
xdm + . . . +
Ω2
R
xdm
Ωn
m
Ω
xT i =
R
xdm
Ωi
mi
=⇒
xT i mi =
Z
xdm
=⇒
Ωi
xT =
n
P
xT i mi
i=1
n
P
i=1
mi
Zjednodušení platí i pro objemy, plochy nebo délky, při splnění podmínek bodů 1, 2,
3.
s01.10. Vázané těleso, vazby a uvolnění
Vazba (mechanická) je spojení mezi tělesy prostřednictvím styku nebo silového pole,
umožňující vzájemné silové působení (interakci).
Protože pohyb je základní vlastností hmoty a tedy i těles, nemůže existovat těleso,
jehož pohybový stav (kterým může být i klid) by nebyl ovlivněn vazbami. Každé těleso
je proto vázané.
Vazby tělesa k okolí lze rozdělit na
a) vazby nerozlišitelné (např. vzájemné gravitační síly mezi tělesy obvyklých strojírenských rozměrů),
b) vazby rozlišitelné, ale z hlediska řešeného problému nepodstatné (např. gravitační síla z hlediska deformace rotujícího rychloběžného kotouče)
c) vazby podstatné.
Uvolňování tělesa je abstraktní proces, při kterém podstatné vazby tělesa nahrazujeme silovým působením při zachování pohybového stavu tělesa.
Poznámka:
Pro uvolněné těleso je v tomto textu používán termín volné těleso (resp. volný prut),
protože je z historických důvodů všeobecně rozšířen.
V dalším textu se budeme zabývat pouze uvolňováním vazeb stykových.
Základní vlastností tělesa je jeho neprostupnost a deformovatelnost, proto stykosilové působení vým útvarem funkční vazby je vždy plošná oblast s rozloženým silovým působením,
~ V D,
na str. 120
které z hlediska statické ekvivalence nahradíme stykovými výslednicemi F~V a M
ekvivalence na kde D je vztažný bod.
str. 122
Jestliže je těleso vázáno více vazbami, pak soustavu rozloženého silového působení při
úplném uvolnění tělesa vyjadřuje soustava silových a momentových stykových výslednic.
Nejjednodušší úlohy statiky lze řešit v rovině se zanedbáním třetího rozměru. Mezi
základní rovinné vazby bez uvažování pasivních odporů patří
–
–
–
–
–
obecná vazba (podpora),
vazba lanem,
rotační vazba,
posuvná vazba,
vetknutí.
126
s01.10.1. Obecná vazba (podpora)
Vazba je charakteristická stykovým útvarem zanedbatelných rozměrů, který nahrazujeme bodem. Omezuje pouze posuv těles ve směru společné normály v místě styku.
schéma vazby
uvolnění
neznámé nezávislé parametry
µ na str. 128
µ = µF = 1
Vazba je podmíněně funkční, výsledná styková síla musí směřovat do tělesa (tlaková).
s01.10.2. Vazba lanem
Kinematické i silové charakteristiky vazby jsou stejné jako u podpory (omezen posuvný
pohyb ve směru osy lana), vazba je rovněž podmíněně funkční, ale výsledná styková
síla musí směřovat ven z tělesa (tahová).
schéma vazby
uvolnění
neznámé nezávislé parametry
µ na str. 128
µ = µF = 1
s01.10.3. Vazba rotační
Stykovým útvarem je kružnice. Rozložené silové působení ve vazbě má směr normály
této kružnice, směřuje tedy do jednoho bodu (centrální rovinná silová soustava). Ome- centrální
souzuje pouze posuvný pohyb ve dvou směrech.
stava na str. 123
schéma vazby
uvolnění
neznámé nezávislé parametry
µ na str. 128
µ = µF = 2
s01.10.4. Posuvná vazba
Stykovým útvarem je úsečka. Omezuje posuv ve směru normály stykové úsečky a otáčení kolem osy kolmé k rovině nákresny. Rozložené silové působení ve stykové oblasti
lze staticky ekvivalentně nahradit silovou a momentovou výslednicí v libovolném bodě
nebo pouze silovou výslednicí (kolmou ke stykové úsečce) v těch bodech, v nichž je
momentová styková výslednice nulová.
schéma vazby
uvolnění
neznámé nezávislé parametry
µ na str. 128
a) µ = 2, µF = 1, µM = 1,
b) µ = 2, µF = 1, µr = 1
Vazba je podmíněně funkční, výsledná styková síla musí směřovat do tělesa
a xA ∈ h0; li.
127
s01.10.5. Vetknutí
Vetknutí omezuje posuvy ve dvou směrech a natočení okolo osy kolmé k nákresně.
schéma vazby
uvolnění
neznámé nezávislé parametry
µ na str. 128
µ = 3, µF = 2, µM = 1
s01.11. Uložení vázaného tělesa
Ve strojírenské praxi jsou tělesa většinou vázána více stykovými vazbami. Soustavu
všech stykových vazeb nazýváme uložením tělesa. Prvkem uložení je vazba neboli
kinematická dvojice.
Uložení lze posat charakteristikami
kinematickými
silovými
- soustavou stupňů volnosti odebraných všemi vazbami,
- soustavou silových a momentových stykových výslednic.
Stupněm volnosti nazýváme nezávislou složku možného pohybu tělesa, který se
obecně skládá z pohybu translačního (přímočarého) a rotačního. Proto volné těleso
má v prostoru 6 stupňů volnosti a v rovině 3.
a) těleso T je vázáno jednou podporou A
vazba omezuje posuv tělesa ve směru
osy x
ξA = 1 (vazba odebírá 1 stupeň volnosti)
b) těleso T je vázáno dvěma podporami B, C
vazby omezují posuv tělesa ve směru osy y a rotaci kolem osy z
ξB = 1, ξC = 1
c) těleso T je vázáno podporami A, B, C
vazby omezují posuvy tělesa ve směru obou os x,
y a rotaci kolem osy z ⇒ těleso je vázáno nepohyblivě
ξA = ξB = ξC = 1
d) těleso T je vázáno podporami A, B, C, D
128
Představíme si, jak by se těleso deformovalo,
kdyby tam vazba D nebyla - - - - . Z obrázku
je patrno, že vazba D funkční je, omezuje 1 deformační parametr - posuv bodu D ve směru
osy y. Tzn. že v tomto případě je těleso uloženo
nepohyblivě, ale má omezený 1 deformační parametr ⇒ to je úloha, která se řeší v předmětu
Pružnost a pevnost“.
” C
e) těleso T je vázáno podporami A, B,
vazby A, C omezují posuvy tělesa ve směru os x,
y, vazba B (je-li funkční, tzn. je-li průměr kruhové části větší než vzdálenost podpor B a C)
omezuje 1 deformační parametr - posuv bodu B
ve směru osy y, i když je těleso uloženo pohyblivě
- může se otáčet kolem osy z. Je to tzv. výjimkový stav uložení.
Normální stav uložení - stykové vazby nejdříve omezují pohyb tělesa jako celku až
do nepohyblivého uložení a teprve pak dochází k omezení deformace (případy a - d).
Pohyblivost vázaného tělesa určíme z kinematického rozboru:
i = iv −
kde
i
P
iv
ξi
η
-
počet
počet
počet
počet
X
ξi + η,
stupňů volnosti vázaného tělesa,
stupňů volnosti volného tělesa,
stupňů volnosti odebraných vazbami,
omezených deformačních parametrů; neznáme-li, dosadíme η = 0.
Výjimkový stav uložení - dříve než je omezen pohyb tělesa jako celku dochází
k omezení deformace (případ e).
Pro nejjednodušší model vazby, který budeme uvažovat, platí, že počet stupňů volnosti odebraných vazbou je roven počtu neznámých nezávislých souřadnic stykových
výslednic
ξ = µ.
Neznámé nezávislé parametry rozlišujeme podle charakteru neznámých souřadnic:
µF - silové,
µM - momentové,
µr - polohové.
Příklad:
Statickým rozborem, který představuje posouzení relací mezi počtem použitelných
podmínek statické rovnováhy ν a počtem neznámých nezávislých parametrů µ můžeme použitelné poddojít k těmto závěrům:
mínky
na
str. 123
129
1. µ > ν
⇒
uložení je staticky neurčité, těleso má omezenou deformaci,
počet neznámých je větší než počet rovnic,
úloha není ve statice jednoznačně řešitelná, řeší se v PP přidáním
vazbových deformačních podmínek,
stupeň statické neurčitosti s = µ − ν.
2. µ < ν
⇒
uložení je staticky přeurčené,
počet neznámých je menší než počet rovnic,
těleso je uloženo pohyblivě, vazby nezajišťují jeho statickou rovnováhu; statické řešení existuje jen pro specifické typy silových soustav
působících na těleso, jinak musíme sestavit pohybové rovnice (úloha
dynamická).
3. µ = ν
⇒
uložení je staticky určité, úloha má jednoznačné statické řešení,
počet neznámých je roven počtu rovnic, což je pouze nutná podmínka statické určitosti, kterou musíme doplnit další podmínkou
µr + µM ≤ νM ;
jednoznačnou, nutnou a postačující podmínkou statické určitosti je při
maticovém zápisu Â~x = ~b podmínka nenulovosti determinantu matice
soustavy  → det  6= 0.
deformační podmínky na str. 43
s01.12. Prutová soustava
Prutové soustavy, kterými se ve statice zabýváme, jsou nejjednodušší modelovou soustavou příhradových konstrukcí.
Příhradová konstrukce je soustava dlouhých
přímých prutů vzájemně nepohyblivě spojených
(svařených, snýtovaných apod.) v tzv. styčnících.
Nejjednodušší příhradová konstrukce v rovině je
tvořena třemi pruty ve tvaru trojúhelníka, v prostoru pak šesti pruty tvořícími hrany čtyřstěnu.
Spojováním těchto nejjednodušších příhrad lze vytvořit příhradovou konstrukci.
Předpoklady prutové soustavy jako modelu příhradové konstrukce jsou:
– Pruty jsou přímé a jejich příčné rozměry jsou zanedbatelné vůči podélným.
– Vnější síly (včetně sil ve vazbách k základnímu tělesu) působí na konstrukci jen
ve styčnících.
– Osy prutů spojených ve styčníku se protínají v jediném bodě.
.
Za těchto předpokladů je ohyb prutů zanedbatelný (Mo = 0), nepohyblivé vazby ve
styčnících je možné nahradit kloubovými (nepřenášejí momenty), tedy rotační vazbou
vazby na str. 126 v rovině a kulovým kloubem v prostoru.
s01.12.1. Statický rozbor prutových soustav
U prutových soustav vyšetřujeme vnější a vnitřní statickou určitost.
130
Nutná podmínka vnější statické určitosti: µex = νcelek
(počet neznámých parametrů stykových sil ve vazbách se základním tělesem je shodný
s počtem použitelných podmínek statické rovnováhy pro prutovou soustavu jako celek).
Nutná podmínka vnitřní statické určitosti:
2k − 3 = p v rovině
3k − 6 = p v prostoru
Příklad 302
(k - počet styčníků, p - počet prutů) - počet použitelných vnitřních podmínek statické Příklad 308
Příklad 303
rovnováhy musí být shodný s počtem neznámých prutových sil, tj. počtem prutů.
– Je-li 2k − 3 > p (resp. 3k − 6 > p), pak prutová soustava
není nepohyblivá a nelze ji uvedeným způsobem řešit.
– Je-li 2k − 3 < p (resp. 3k − 6 < p), pak je prutová soustava staticky neurčitá a dá se řešit jedině metodami PP
(přidáním vazbových deformačních podmínek).
s01.12.2. Řešení statické rovnováhy prutových soustav
Při splnění všech výše uvedených předpokladů přenáší
každý prut jen sílu v ose prutu, je tedy namáhán pouze
tahem nebo tlakem. Jeho uvolnění je triviální a obvykle
je nekreslíme.
Pouze si všimněme, že síla je zavedena ven
z prutu, aby v něm vyvolávala kladnou normálovou sílu podle konvencí prostého tahu.
Styčníky (tj. rotační vazby mezi pruty) považujeme za samostatná tělesa. Při jejich uvolnění je nutné podle zákona akce a reakce zavádět síly v prutech směrem ven ze styčníku.
V každém styčníku vznikne uvolněním centrální silová soustava. Pro ni sestavíme rovnice
statické rovnováhy a řešíme některou z následujících metod.
a) Obecná styčníková metoda
Spočívá v uvolnění všech styčníků a sestavení použitelných podmínek statické
rovnováhy. Dostaneme soustavu lineárních algebraických rovnic, kterou řešíme na
počítači.
b) Postupná styčníková metoda
Spočívá v postupném uvolňování jednotlivých styčníků. Pro každý styčník se ihned
sestavují a řeší rovnice statické rovnováhy. Proto pořadí styčníků není libovolné,
ale je dáno podmínkou, že na uvolněný styčník působí kromě úplně určených sil
neúplně určené síly pouze se 3 neznámými parametry u prostorové resp. se 2 neznámými parametry u rovinné prutové soustavy.
131
deformační podmínka na str. 43
Literatura
[1] Janíček P., Ondráček E., Vrbka J.: Mechanika těles. Pružnost a pevnost I. VUT
v Brně, 1992.
[2] Ondráček E., Vrbka J., Janíček P.: Mechanika těles. Pružnost a pevnost II. VUT
v Brně, 1991.
[3] Florian Z., Ondráček E., Přikryl K.: Mechanika těles. Statika. VUT v Brně, 1992.
[4] Janíček P., Florian Z.: Mechanika těles. Úlohy z pružnosti a pevnosti I. VUT
v Brně, 1990.
[5] Vlk M.: Mezní stavy a spolehlivost. VUT v Brně, 1991.
[6] Pokluda J., Kroupa F., Obdržálek L.: Mechanické vlastnosti a struktura pevných
látek. VUT v Brně, 1994.
[7] Peterson R.E.: Stress Concentration Factors. John Wiley & Sons, New York 1973.
132
Rejstřík
statická, 122
energie
napjatosti, 30, 31, 55, 56, 73,
74, 81, 86, 88, 110
měrná, 55, 74
ULOŽENÍ
uložení, 49
A
analýza deformačně-napěťová, 1, 2
B
bezpečnost, 65, 95, 104
obecná, 109
prostá, 106, 108
bod
bifurkace, 93
inflexní, 47
nebezpečný, 45, 55, 65, 75, 81,
103
rozdvojení rovnováhy, 93, 96
F
funkcionál, 110
H
houževnatost lomová, 8
hustota energie napjatosti, 55
hyperbola Eulerova, 96
Ch
charakteristiky
deformační, 19, 82
geometrické, 38
materiálové, 4, 104, 105, 107
průřezové, 86
C
creep, 8
Č
čára ohybová, 82, 83, 88, 93
číslo Poissonovo, 33, 56
I
interakce, 126
invariant tenzoru napětí, 98
D
deformace, 18, 21, 56, 74, 75, 83,
89, 120
malá, 83
nevratná, 6
plastická, 6, 32
pružná, 6, 23, 33
pružně plastická, 34
smyková, 72
trojosá, 53, 79
trvalá, 6, 32
v bodě, 19, 20
vratná, 6
délka kritická, 9
deska rotačně symetrická, 12
dilatace teplotní, 66
dráha
zatěžovací, 105
dvojice silová, 84
K
koncentrace
napětí, 60, 61, 77, 84, 113
přetvoření, 60, 77, 113
konstanta Lamého, 25
konstrukce
příhradová, 130
kontrakce, 34
konvence znaménková, 15, 43, 59
koroze, 8
kořen vrubu, 84
krut, 37, 42, 71, 72, 75, 76
kružnice Mohrova, 41, 58
křivka
Mansonova – Coffinova, 8
obrysová, 36, 85
Wöhlerova, 8
L
lom, 113
creepový, 8
korozí pod napětím, 8
E
ekvivalence
pohybová, 121
133
osový, 38, 39
polární, 38, 39, 73
lineární, 38
ohybový, 42, 78, 84, 92
síly k bodu, 122
síly k ose, 122
statický, 38
montážní
vůle, 89
křehký, 8, 35, 61, 96
nestabilní, 8
tvárný, 7, 34, 35
únavový, 8
M
materiál
hookovský, 23, 54, 72, 79
houževnatý, 34, 61, 96
izotropní, 24, 54, 104
křehký, 35, 61, 96
lineárně pružný, 23
pružně plastický, 32
s lineárním zpevněním, 32
matice
elastických modulů, 24
metoda
analytická, 110
experimentální, 113
konečných prvků, 110
variační, 110
mez
kluzu, 34, 35, 104
dolní, 33
horní, 33
ve smyku, 76, 106, 108
křehké pevnosti, 61
v tahu, 35
v tlaku, 35
pevnosti, 34
pevnosti materiálu, 8
pevnosti při tečení, 8
únavy materiálu, 8
MKP, 65, 110
modelování výpočtové, 3
modul
průřezu
v krutu, 73
v ohybu, 81
pružnosti
v tahu, 24, 33
ve smyku, 24
Youngův, 24
moment
kroutící, 42, 71
kvadratický, 38–40
deviační, 38, 39
hlavní, 40
hlavní centrální, 40, 95
N
namáhání, 22
jednoduché, 43, 91
kombinované, 43, 63, 91, 104
krutem, 22, 42
ohybem, 22, 42, 86, 104
prosté, 48, 65
smykem, 22, 42
tahem, 22, 42, 56, 60, 66, 104
tlakem, 42
ideální, 92
napětí, 54, 72, 73, 75, 79, 80
hlavní, 57, 98, 99
lomové kritické, 8
nominální, 61, 77, 84, 113
normálové, 14, 57, 72, 79, 85,
98
obecné, 10, 11, 42, 57, 58, 98
redukované, 106, 108
smykové, 14, 15, 57, 59, 60, 72,
73, 79, 85, 105
smluvní, 85
napjatost, 14, 21, 57, 58, 98, 100
dvojosá, 101
homogenní, 15, 57, 84
hydrostatická, 101
jednoosá, 54, 55, 81, 82, 96,
102, 104–107
homogenní, 63
nehomogenní, 79
obecná, 100, 103, 105
prutová, 37, 101, 103, 104, 106,
108
reziduální, 32
rovinná, 101
obecná, 101
rovnoměrná, 101
smyková, 72, 74, 102–104, 106,
108
134
Trescova, 105
spojitosti, 88
statické, 123
ekvivalence, 79, 122
použitelné, 123
rovnováhy, 42, 49, 52, 123
triviální, 123
určitosti, 130
vazbové, 47, 48, 50, 66, 76, 87
podpora, 127
pohyb, 120
pohyblivost, 129
Poissonovo číslo, 24
porušení, 120
posuv, 19, 41, 64
deformační, 18, 20, 53
práce deformační, 27, 28, 30, 55,
73, 81
princip Saint Venantův, 13, 16,
90
prostor Haighův, 105
průhyb, 19, 82, 89, 95
průřez
kritický, 7
nebezpečný, 43, 52, 65, 75
nesouvislý, 36
souvislý, 36
prut, 12, 36, 44, 48, 104
ideální, 95
lomený, 89, 90
neprizmatický, 52
otevřený, 49, 51
prizmatický, 53, 82
přímý, 51
uzavřený, 51
vázaný, 65, 76, 89
volný, 64, 75, 87, 95
zakřivený, 51, 63, 86, 89, 90
silně, 86
slabě, 86
pružnost
I. řádu, 13
II. řádu, 13, 43
lineární, 23, 26, 89
nelineární, 23
obecná, 13, 85
prostá, 13
prutů, 85
prvek, 10
tahová, 102
tělesa, 15, 16
tlaková, 102
trojosá, 34, 61, 100, 105
obecná, 60, 100, 113
polorovnoměrná, 100
rovnoměrná, 101
v bodě, 15
vlastní, 21
zbytková, 21, 32
natočení, 89
nauka o mezních stavech, 1, 2
nelinearita, 23
nosník, 85
O
odlehčování, 103
ohyb, 37, 42, 92
obecný, 78, 80
prostý, 82
základní, 78, 81, 82, 86
osa
centrální, 38, 40
hlavní, 40
centrální, 40, 41, 61
neutrální, 80, 82, 85, 86, 95
osazení, 113
P
parametr
deformační, 49, 129
vazbový, 48
plocha plasticity, 105
počet variační, 110
poddajnost, 48
podmínky
deformační, 11, 48, 50, 51, 66,
68, 69
homogenní, 50, 66
nehomogenní, 50, 66
podmíněné, 50
vazbové, 49
hladkosti, 88
lineárně
nezávislé, 123
závislé, 123
okrajové, 23, 87
plasticity, 104, 105
max τ , 76, 105
HMH, 107, 108
135
objemová, 62
osamělá, 21
posouvající, 42
prutová, 67
styková, 52
vnitřní, 10, 11, 42
skořepina
bezmomentová, rotačně symetrická, 12
momentová, válcová, 12
smyk, 37, 42
součinitel
koncentrace napětí, 61, 77, 84,
113
Poissonův, 24, 56
příčinkový, 27
příčné kontrakce, 24
teplotní roztažnosti, 65
součinitel bezpečnosti, 103, 104,
106, 107
soustava
prutová, 66, 68, 69, 130
prutů, 66–68
staticky
neurčitá, 67–69
neurčitá vně, 69
neurčitá vnitřně, 69
určitá, 67, 68
určitá vně, 68
určitá vnitřně, 68
spolehlivost, 103
stabilita vzpěrná, 92
statická
neurčitost, 49
určitost, 48
statika, 2, 18
stav
lineárně pružný, 30
mezní, 5, 16, 17, 19, 22, 55, 57,
103, 104
deformace, 5, 6, 65
deformační stability, 7
křehké pevnosti, 104
porušení, 3, 5, 7, 8, 34
pružnosti, 6, 21, 32, 65, 96,
97, 103–105
vzpěrné stability, 7, 92, 95–97
montážní, 21
nezatížený, 21
elementární
dvojnásobně, 10, 12, 13
jednonásobně, 10, 12, 13, 37
trojnásobně, 10, 12
konečný, 10, 37
předpoklady
bezmomentovosti, 12
prutové, 12, 36, 82
deformační, 37
geometrické, 36, 87
napjatostní, 37
vazbové, 36
zatěžovací, 36
přetvoření, 20, 64
délkové, 20, 33, 53, 56, 71, 78,
82
příčné, 56
úhlové, 20, 53, 72, 73, 78
přístup
diferenciální, 45, 52, 87, 88
experimentální, 3
integrální, 44, 52, 87–89
intuitivní, 2
výpočtový, 3
R
rovina
hlavní, 57, 98, 99
Mohrova, 58, 72
neutrální, 82
oktaedrická, 99, 107
rovnice
charakteristická, 98
ohybové čáry, 83
rovnováha
statická, 123
rovnováha statická, 10, 42
rozbor
kinematický, 129
statický, 123, 129
Ř
řešení Lagrangeovo, 93
S
síla, 121
doplňková, 89
hnací, trhliny, 8
kritická vzpěru, 7, 93
normálová, 42, 62, 92
136
těžiště, 38, 41–43, 54, 55, 125
tlak, 42, 53
transformace
natočením, 40
posunutím, 40
trhlina, 7, 18
křehká, 35, 61
tuhost, 48
příčného průřezu
v krutu, 74
v tahu, 56
provozní, 21
pružně plastický, 32
pružný, 27
přechodový, 5, 21, 22
uložení
normální, 129
výjimkový, 129
výchozí, 21
výrobní, 21
zatěžovací, 21
stěna rotačně symetrická, 12
střednice, 36, 38, 43, 45, 52, 90
stupeň
statické neurčitosti, 49, 66, 130
volnosti, 129
stupeň volnosti, 128
styčník, 67, 130, 131
styčníková metoda
obecná, 68, 131
postupná, 68, 131
superpozice
deformace, 26
napjatosti, 26
systém kartézský, 14
systém souřadnicový
centrální, 79
globální, 44, 45
hlavní, 40, 57, 98
centrální, 81
hlavní centrální, 40, 41, 80
kartézský, 36
lokální, 42, 43
Ú
účinky
silové vazbové, 49
výsledné vnitřní, 41–43
úhel
natočení, 19, 30, 31, 74, 75
zkroucení, 74
poměrný, 72, 73
úhel natočení, 82
úloha
lineární, 23
nelineární pružnosti, 23
pružnosti, 41
uložení, 128
staticky
neurčité, 49, 50, 130
přeurčené, 130
určité, 49, 130
vně neurčité, 51
vně určité, 131
vnitřně neurčité, 51
výjimkové, 129
únava materiálu, 8
úroveň rozlišovací, 4
uvolnění, 52, 126
částečné, 49, 50, 66, 68, 69
tělesa, 126
úplné, 50, 66
Š
šroubovitost, 61
štíhlost prutu, 96
T
tah, 37, 42, 53, 60, 62
tečení, 8
těleso
izotropní, 30
lineárně pružné, 27, 28, 31
modelové, 11
prutové, 69
tlustostěnné, 12
tenzor
deformace, 20
napětí, 14, 15, 54, 57, 72, 98
přetvoření, 20, 53, 72, 79, 111
V
vazba, 47, 67, 126
lanem, 127
lineárně pružná, 48
obecná, 127
podmíněně funkční, 127
posuvná, 127
rotační, 127
tuhá, 48
137
vetknutím, 128
věta
Bettiho, 26–28
Castiglianova, 29–31, 68, 86,
88, 89
o minimu kvadratického funkcionálu, 110
o sdruženosti smykových napětí, 15, 59, 60, 72
o vzájemnosti prací, 26
Schwedlerova, 45–47, 52
Steinerova, 40
vrub, 60, 61, 77, 84, 113
vůle montážní, 66
VVÚ, 22, 41, 46, 51
vzorec Žuravského, 85
vzpěr, 13
vztahy
geometrické, 53, 71, 78
konstitutivní, 72
vztahy konstitutivní, 33, 74
Z
zákon Hookův, 23, 25, 54
obecný, 24
zobecněný, 25
zápich, 113
zatěžování, 103
prosté, 108
zatížení, 21
deformační, 21
liniové, 21, 85, 121
monotonně rostoucí, 104
objemové, 21, 121
plošné, 21, 121
příčné, 85
silové, 21
spojité, 52
tahové, 63
teplotní, 21
vnější, 89
vnitřní, 42
zkos, 20, 24
zkouška
tahová, 33, 35
tlaková, 34, 35
zlom, 90
138
Podobné dokumenty
ohyb
 a musíme ji počítat pomocí vztahů pro pruty zakřivené (ty nejsou součástí bakalářského studia PP) nebo
dnes častěji metodou konečných prvků.
a musíme ji počítat pomocí vztahů pro pruty zakřivené (ty nejsou součástí bakalářského studia PP) nebo
dnes častěji metodou konečných prvků.
bulletin 3·2014 - Česká společnost pro mechaniku
 v němž je průhyb pod působící silou vyjádřen jako funkce působící síly,
geometrických rozměrů nosníku a materiálových vlastností, charakterizovaných
Youngovým modulem pružnosti. Pro tzv. tenký nosn...
v němž je průhyb pod působící silou vyjádřen jako funkce působící síly,
geometrických rozměrů nosníku a materiálových vlastností, charakterizovaných
Youngovým modulem pružnosti. Pro tzv. tenký nosn...
Modelování proudění vody na měrném přelivu
 Experimentální povodí Modrava 2 se nachází na severním svahu Malé
Mokrůvky v pramenné oblasti Ptačího potoka (hydrologické pořadí povodí 108-01-002), 5 km jižně od Filipovy Huti, na hranici s Bavor...
Experimentální povodí Modrava 2 se nachází na severním svahu Malé
Mokrůvky v pramenné oblasti Ptačího potoka (hydrologické pořadí povodí 108-01-002), 5 km jižně od Filipovy Huti, na hranici s Bavor...
Obráběcí stroje a příslušenství
 nástroj pohybuje někdy i v několika cyklech nad povrchem polotovaru. Díky měřicí sondě lze s použitím velmi jednoduché
logiky větvení programu dosáhnout produktivního obrábění bez ohledu na velikos...
nástroj pohybuje někdy i v několika cyklech nad povrchem polotovaru. Díky měřicí sondě lze s použitím velmi jednoduché
logiky větvení programu dosáhnout produktivního obrábění bez ohledu na velikos...
Metody výstavby budov ze dřeva
 Prostorová tuhost budovy s lehkým skeletem je zajišťována ztužením konstrukce stropu a stěn.
Stropní konstrukce se ztuží tak, že se stropnice vzájemně rozepřou (ztuží) na vzdálenost asi 2 m.
Rozměr...
Prostorová tuhost budovy s lehkým skeletem je zajišťována ztužením konstrukce stropu a stěn.
Stropní konstrukce se ztuží tak, že se stropnice vzájemně rozepřou (ztuží) na vzdálenost asi 2 m.
Rozměr...
Experimentální studium vodíkových vazeb
 25,26-dipropoxy-5,11,17,23-tetra-tert-butylkalix[4]aren je odvozen od kalix[4]arenu
substitucí ty tert-butyl na horním a dvou propyl umíst ných proximáln na spodním
okraji. Ze ty základních konform...
25,26-dipropoxy-5,11,17,23-tetra-tert-butylkalix[4]aren je odvozen od kalix[4]arenu
substitucí ty tert-butyl na horním a dvou propyl umíst ných proximáln na spodním
okraji. Ze ty základních konform...
Kombinované namáhání 1
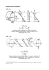 Ohybové nap tí se m ní po pr!"ezu lineárn – maxima v bodech A a B.
Smykové nap tí se m ní lineárn – max. na obvodu, min. ve st"edu.
Nebezpe#ná místa - A a B.
Ohybové nap tí se m ní po pr!"ezu lineárn – maxima v bodech A a B.
Smykové nap tí se m ní lineárn – max. na obvodu, min. ve st"edu.
Nebezpe#ná místa - A a B.
STATISTIKA - Polodriver
 Distanční vysokoškolské studium je specifická forma, která v případě předmětu Statistika vyžaduje enormní úsilí studenta zaměřené na pravidelnost a vytrvalost v samostudiu, schopnost koncentrace na...
Distanční vysokoškolské studium je specifická forma, která v případě předmětu Statistika vyžaduje enormní úsilí studenta zaměřené na pravidelnost a vytrvalost v samostudiu, schopnost koncentrace na...