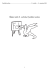hc01 Teorie a řízení portfolia

INSTITUT EKONOMICKÝCH STUDIÍ
Fakulta sociálních věd University Karlovy
Teorie a řízení portfolia
Studijní text č. 1 k předmětu Řízení finančních rizik
Přednášející: doc. Ing. Oldřich Dědek, CSc.
2
A. ZÁKLADY TEORIE PORTFOLIA
1. Funkce očekávaného užitku
a) rizikové a bezrizikové aktivum
bezrizikové aktivum (riskless asset) je aktivum, jehož budoucí hodnota je známá čili
je nezávislá na konkrétní realizaci budoucího stavu světa
I … aktuální hodnota bezrizikového aktiva
W …budoucí hodnota bezrizikového aktiva
µF =
W −I
… bezriziková výnosová míra
I
rizikové aktivum (risky asset) je náhodná veličina, jejíž budoucí hodnota závisí na
konkrétní realizaci budoucího stavu světa
I … aktuální hodnota rizikového aktiva
~
W .. budoucí hodnota rizikového aktiva jako náhodná veličina, která
s pravděpodobností p s realizace s-tého stavu světa nabývá hodnotu Ws
~
~ W −I
… výnosová míra (náhodná veličina)
R=
I
~
E (W ) = ∑ p sWs … očekávaná hodnota rizikového aktiva
s
~
E (W ) − I
µ=
… očekávaná výnosová míra rizikového aktiva
I
b) averze vůči riziku
Obrázek: Užitková funkce investora s averzí vůči riziku
U
U (WF ) = E[U (WF )]
~
E[U (W )] = p1U (W1 ) + p 2U (W2 )
~
E (W ) = p1W1 + p 2W2 = WF = E (WF )
πA
W1
WF = E(W)
W2
3
investor s averzí vůči riziku je takový investor, který mezi rizikovým a bezrizikovým
aktivem, z nichž obě generují stejnou očekávanou hodnotu, preferuje bezrizikové
aktivum před rizikovým
averze vůči riziku je výsledkem klesající funkce mezního užitku ( U ' (W ) < 0 )
~
očekávaný užitek rizikového aktiva = E[U (W )] = p1U (W1 ) + p 2U (W2 ) <
< U ( p1W1 + p 2W2 ) = U (W f ) = (očekávaný) užitek bezrizikového aktiva
~
rozlišuj: - hodnota očekávaného užitku E[U (W )]
~
- užitek očekávané hodnoty U ( E (W ))
absolutní averze k riziku ( π A ): o jakou částku je investor ochoten snížit očekávanou hodnotu
rizikového aktiva (jak velké je ochoten zaplatit pojistné) výměnou za to, že nebude vystaven
riziku
~
~
E[U (W )] = U ( E (W ) − π A )
πA = −
σ Z2 U ' ' ( µW )
~
~ ~
, µW = E (W ), Z = W − µW
2 U ' ( µW )
výraz ( − U ' ' / U ' ) se nazývá koeficient absolutní averze k riziku a jeho reciproká hodnota se
nazývá koeficient tolerance rizika
návod k odvození:
~
~
~
~
E[U (W )] = E[U ( µW + Z )] =& E[U ( µW ) + U ' ( µW ) Z + 12 U ' ' ( µW ) Z 2 ]
U ( µW − π A ) =& U ( µW ) − U ' ( µW )π A
relativní averze k riziku ( π R ): o jakou procentuální část je investor ochoten snížit očekávanou
hodnotu rizikového aktiva výměnou za to, že nebude vystaven riziku
~
~
E[U (W )] = U [ E (W )(1 − π R )]
σ Z2 µW U ' ' ( µW )
πR = −
2 U ' ( µW )
výraz ( − µW U ' ' / U ' ) se nazývá koeficient relativní averze k riziku
investor milující riziko je takový investor, který mezi rizikovým a bezrizikovým aktivem,
z nichž obě generují stejnou očekávanou hodnotu, preferuje rizikové aktivum (důsledek
rostoucí funkce mezního užitku)
4
investor neutrální vůči riziku je takový investor, který je indiferentní mezi rizikovým a
bezrizikovým aktivem, pokud obě aktiva generují stejnou očekávanou hodnotu
(důsledek konstantní funkce mezního užitku)
c) rozhodování v prostoru očekávaného výnosu a rizika
- vyjádření užitku jako funkce očekávaného výnosu aktiva
~
~
~
E[U (W )] = E[U ( I (1 + R ))] = E[u ( R )]
~
- Taylorův rozvoj druhého řádu v bodě očekávaného výnosu µ = E (R )
u ( R ) = u ( µ ) + u ' ( µ )( R − µ ) + 12 u ' ' ( µ )( R − µ ) 2
- dosazení Taylorova rozvoje do funkce očekávaného užitku
~
~
~
E[u ( R )] = u ( µ ) + u ' ( µ ) E ( R − µ ) + 12 u ' ' ( µ ) E ( R − µ ) 2
= u ( µ ) + 12 u ' ' ( µ )σ 2 = Φ ( µ , σ )
~
σ 2 = E ( R − µ ) 2 … velikost rizika měřená rozptylem očekávaných
výnosů
σ = σ 2 … velikost rizika měřená směrodatnou odchylkou
očekávaných výnosů
- vlastnosti indiferenční křivky Φ ( µ , σ ) = konst . (za předpokladu nulové třetí derivace)
i) indiferenční křivka je rostoucí
dµ
∂Φ / ∂σ
u' ' (µ )
σ , proto
=−
=−
dσ
∂Φ / ∂µ
u' (µ )
u ' > 0, u´´< 0 ⇒
dµ
>0
dσ
Obrázek: Indiferenční mapa v prostoru výnosu a rizika
µ
Φ2
Φ1
Φ0
σ
5
ii) indiferenční křivka je konvexní
indiferenční křivku lze chápat jako jistý funkční vztah µ = µ (σ ) , přičemž
dµ / dσ = µ ' > 0, dle předpokladu u ' ' ' = 0
d
dσ
2
⎛ dµ ⎞ d ⎛ u ' ' ( µ ) ⎞ (u ' ' ' µ 'σ + u ' ' )u '−(u ' ' ) σµ '
⎜⎜ −
>0
σ ⎟⎟ =
⎜
⎟=
(u ' ) 2
⎝ dσ ⎠ dσ ⎝ u ' ( µ ) ⎠
2. Množina investičních příležitostí
parametry rizikového aktiva:
~
Ri … výnos rizikového aktiva (náhodná veličina, jejíž hodnota závisí na
realizaci budoucího stavu světa)
~
µ i = E ( Ri ) … očekávaný výnos rizikového aktiva
~
σ i2 = E ( Ri − µ i ) 2 …riziko aktiva měřené rozptylem náhodného výnosu okolo
očekávané hodnoty
parametry portfolia rizikových aktiv:
N
~
~
R P = ∑ θ i Ri … výnos portfolia (náhodná veličina závislá na velikosti výnosů
i =1
složkových aktiv)
N
~
µ P = E ( R P ) = ∑ θ i µ i … očekávaný výnos portfolia
i =1
N … počet aktiv v portfoliu
θi … váha i-tého aktiva v portfoliu (podíl hodnoty aktiva na
celkové hodnotě portfolia)
σ P2 … riziko portfolia (měřené rozptylem výnosů)
[
]
2
⎡N
⎤
~
~
σ = E ( R P − µ P ) 2 = E ⎢ ∑ θ i ( Ri − µ i ) ⎥
⎣ i =1
⎦
N
N
⎡
⎤ N
~
~
= E ⎢∑∑ θ iθ j ( Ri − µ i )( R j − µ j )⎥ = ∑ θ i2σ i2 + 2∑ θ iθ j σ ij
i< j
⎣ i =1 j =1
⎦ i =1
2
P
N
= ∑ θ i2σ i2 + 2∑ θ iθ j σ iσ j ρ ij
i =1
i< j
6
[~
]
~
⎡ ~
N
⎣
i =1
~
⎤
σ P2 = E ( RP − µ P )( R P − µ P ) = E ⎢( RP − µ P )∑ θ i ( Ri − µ i )⎥
[
N
]
⎦
N
~
~
= ∑ θ i E ( R P − µ P )( Ri − µ i ) = ∑ θ iσ iP
i =1
i =1
σ ij …. kovariance výnosů i–tého a j–tého rizikového aktiva
~
~
σ ij = E[( Ri − µ i )( R j − µ j )] = σ iσ j ρ ij
σ iP …. kovariance výnosů i–tého aktiva a rizikového portfolia
⎡ ~
N
⎣
j =1
~
⎤
N
⎦
j =1
[~
~
σ iP = E ⎢( Ri − µ i )∑ θ j ( R j − µ j )⎥ = ∑ θ j E ( Ri − µ i )( R j − µ j )
]
N
= ∑ θ j σ jP
j =1
ρ ij … korelační koeficient výnosů i–tého a j–tého rizikového aktiva (nabývá
hodnoty z intervalu 〈− 1,1〉
ρ ij =
σ ij
σ iσ j
♦
Portfolio je složeno ze dvou rizikových aktiv, která vykazují následující parametry:
µ1 = 20 %, σ 1 = 75 %, θ 1 = 40 %,
µ 2 = 16 %, σ 2 = 50 %, θ 2 = 60 %,
ρ12 = −60 %.
Dostáváme
µ P = 0,4 × 0,2 + 0,6 × 0,16 = 17,6 %
σ P2 = 0,4 2 × 0,75 2 + 0,6 2 × 0,5 2 − 2 × 0,4 × 0,6 × 0,75 × 0,5 × 0,6 = 0,072
σ P = 0,072 = 27 %
Portfolio dosahuje podstatně nižšího rizika při srovnání s rizikem obou individuálních aktiv
(projev efektu diverzifikace).
♦
maticový tvar výpočtu rizika
matice volatilit V:
0⎤
⎡σ 1 0
⎢
V = ⎢ 0 σ 2 0 ⎥⎥
⎢⎣ 0 0 σ 3 ⎥⎦
7
matice korelačních koeficientů C:
⎡ 1
C = ⎢⎢ ρ12
⎢⎣ ρ13
ρ12
1
ρ 23
ρ13 ⎤
ρ 23 ⎥⎥
1 ⎥⎦
varianční-kovarianční matice VCV:
⎡σ 12 σ 12 σ 13 ⎤
⎢
⎥
VCV = ⎢σ 12 σ 22 σ 23 ⎥ = V × C × V
⎢σ 13 σ 23 σ 32 ⎥
⎣
⎦
váhová matice W:
W = [θ1 θ 2 θ 3 ]
riziko portfolia σ P2 :
σ P2 = W × (VCV ) × W '
množina investičních příležitostí (opportunity set) je množina všech kombinací očekávaného
výnosu a rizika dosažitelná různým váhovým zastoupením složkových aktiv daného
portfolia
a) dokonalá kladná korelace výnosů aktiv ( ρ12 = 1 )
µ P = θ 1 µ1 + θ 2 µ 2
σ P = θ12σ 12 + θ 22σ 22 + 2θ 1θ 2σ 1σ 2 × 1
= (θ1σ 1 + θ 2σ 2 ) 2 = θ1σ 1 + θ 2σ 2
Obrázek: Množina investičních příležitostí dokonale kladně korelovaných aktiv
µP
µ2
µ1
A2
S
σ2
σP
A1
σ1
8
množina investičních příležitostí má tvar přímky
θ1 = 0 ⇒ portfolio je tvořeno pouze aktivem A2
θ 2 = 0 ⇒ portfolio je tvořeno pouze aktivem A1
pokračování přímky za body A1 , A2 je dosažitelné krátkým prodejem příslušného
aktiva (portfolio S je např. tvořeno vahami θ1 = −30 %, θ 2 = 130 % )
♦
Pokud aktiva z předchozího přikladu vykazují dokonalou kladnou korelaci očekávaných
výnosů, bude mít portfolio s uvedeným váhovým zastoupením složkových aktiv následující
parametry:
µ P = 0,4 × 0,2 + 0,6 × 0,16 = 17,6 %
σ P = 0,4 × 0,75 + 0,6 × 0,5 = 60 %
Efekt diverzifikace se neprojevuje, vyšší očekávaný výnos je doprovázen vyšším rizikem.
♦
objasnění záporných vah krátkého prodeje:
- při sestavení portfolia bez krátkého prodeje je počáteční investice I 0 alokována mezi
složková aktiva v objemech I 10 a I 20 , neboli I 0 = I 10 + I 20
- na konci období obě aktiva dosahují jisté hodnoty I i1 , načež pro výnos portfolia lze
psát
RP =
(
) (
)
I 11 + I 21 − I 10 + I 20
I 10 I 11 − I 10 I 20 I 21 − I 20
I1 − I 0
=
=
×
+ 0×
= θ 1 R1 + θ 2 R2
I0
I0
I0
I 10
I
I 20
0 ≤ θ1 ≤ 1 a 0 ≤ θ 2 ≤ 1
- při krátkém prodeji prvního aktiva je počáteční disponibilní částka I 0 posílena o
příjem z prodeje vypůjčeného prvního aktiva a takto posílená částka je celá
alokována do druhého aktiva, neboli I 0 + I 10 = I 20 .
- na konci období musí být část druhého aktiva prodána z důvodu zakoupení a vrácení
vypůjčeného prvního aktiva, neboli I 1 = I 21 − I 11
(
) (
)
I 21 − I 11 − I 20 − I 10
I 10 I 11 − I 10 I 20 I 21 − I 20
I1 − I 0
RP =
=
=− 0×
+ 0×
= θ1 R1 + θ 2 R2
I0
I0
I
I 10
I
I 20
θ1 ≤ 0 a θ 2 ≥ 1
9
b) dokonalá záporná korelace výnosů aktiv ( ρ12 = −1 )
µ P = θ 1 µ1 + θ 2 µ 2
σ P = θ12σ 12 + θ12σ 12 − 2θ 1θ 2σ 1σ 2
= (θ1σ 1 − θ 2σ 2 ) 2 = θ1σ 1 − θ 2σ 2
Obrázek: Množina investičních příležitostí dokonale záporně korelovaných aktiv
µP
A2
µ2
H
A1
µ1
σ1
σ2
σP
množina investičních příležitostí má tvar zalomené přímky
existuje kombinace rizikových aktiv H s výsledným nulovým rizikem, které
odpovídá váhové zastoupení složkových aktiv v poměru
θ1 =
σ2
σ1
, θ2 =
σ1 + σ 2
σ1 + σ 2
⇒σH = 0
efektivní množina investičních příležitostí (effective opportunity set) je množina všech
nedominovaných portfolií, tj. takových portfolií, k nimž neexistuje portfolio s vyšším
výnosem při stejném riziku resp. portfolio s nižším rizikem při stejném výnosu
♦
Pokud aktiva z předchozího příkladu vykazují dokonale zápornou korelaci očekávaných
výnosů, bude mít portfolio s uvedeným váhovým zastoupením obou dvou složkových aktiv
následující parametry:
µ P = 0,4 × 0,2 + 0,6 × 0,16 = 17,6 %
σ P = 0,4 × 0,75 − 0,6 × 0,5 = 0 %
♦
10
c) nekorelované výnosy aktiv ( ρ12 = 0 )
µ P = θ 1 µ1 + θ 2 µ 2
σ P = θ 12σ 12 + θ 12σ 12
Obrázek: Množina investičních příležitostí nekorelovaných aktiv
µP
A2
µ2
H
A1
µ1
σ1
σ2
σP
množina investičních příležitostí má tvar paraboly
existuje kombinace rizikových aktiv H s minimálním rizikem, které odpovídá
váhové zastoupení složkových aktiv v poměru (lze získat řešením rovnice
∂σ P ∂θ1 = 0 )
θ1 =
σ 12
σ 22
=
,
θ
2
σ 12 + σ 22
σ 12 + σ 22
existuje efektivní část množiny investičních příležitostí (horní větev paraboly) a
neefektivní část této množiny (dolní větev paraboly)
♦
Pokud aktiva z předchozího příkladu vykazují neexistující korelaci očekávaných výnosů,
bude mít portfolio s uvedeným váhovým zastoupením obou dvou složkových aktiv následující
parametry:
µ P = 17,6 %
σ P = 0,4 2 × 0,75 2 + 0,6 2 × 0,5 2 = 42 %
Pro vytvoření portfolia s minimálním rizikem je nutné kombinovat aktiva v poměru
0,5 2
θ1 =
= 31 %, θ 2 = 1 − 0,31 = 69 %
0,75 2 + 0,5 2
♦
11
d) velký počet rizikových aktiv
množinu investičních příležitostí tvoří portfolia (jako dvojice výnosu a rizika
( µ P , σ P ) ), sestavitelná všemi možnými váhovými zastoupeními existujících
složkových aktiv
N
µ P = ∑θ i µ i
i =1
σP =
N
N
∑∑θ θ σ σ
i =1 j =1
i
j
i
j
ρ ij
Obrázek: Hranice investičních příležitostí při velkém počtu rizikových aktiv
A
µP
•
H
•
•
•
•
•
•
σP
hranici efektivních příležitostí tvoří konkávní spojnice bodu H (portfolio
s minimálním rizikem) a bodu A (aktivum s nejvyšším očekávaným výnosem)
- existuje efektivní část hranice, všechny ostatní vnitřní a hraniční body
reprezentují neefektivní čili dominovaná portfolia
- důležitý předpoklad homogenních očekávání (názorová shoda všech
investorů na velikost očekávaného výnosu a rizika všech aktiv)
e) efektivní množina při existenci bezrizikového aktiva
i) jedno bezrizikové a jedno rizikové aktivum
µP = θF µF + θM µM
σ P = θ M2 σ M2 = θ M σ M
12
Obrázek: Množina investičních příležitostí s rizikovým a bezrizikovým aktivem
µP
M
µM
µF
F
σM
σP
v bodě F je portfolio tvořeno výlučně bezrizikovým aktivem, v bodě M výlučně
rizikovým aktivem
body ležící na úsečce FM představují investici do bezrizikového aktiva čili
zapůjčení peněz za bezrizikovou sazbu
body ležící za bodem M představují krátký prodej bezrizikového aktiva čili
vypůjčení peněz za bezrizikovou sazbu za účelem zakoupení rizikového aktiva
ii) jedno bezrizikové a mnoho rizikových aktiv
Obrázek: Přímka kapitálového trhu
CML
µP
µM
µF
M
•
A
F
σM
σP
efektivní množina má tvar přímky, která prochází bodem bezrizikového aktiva F a
bodem dotyku M této přímky s množinou investičních příležitostí (jakékoli jiné
rizikové portfolio A je dominováno nějakým bodem této přímky)
přímka kapitálového trhu (capital market line, CML) je název této lineární efektivní
13
množiny
tržní portfolio je název bodu dotyku přímky kapitálového trhu a množiny rizikových
investičních příležitostí
rovnice přímky CML:
µP = µF +
µM − µF
×σ P , σ P = θMσ M
σM
výnos efektivního portfolia = bezrizikový výnos + tržní cena rizika × množství
rizika
µP − µF =
µM − µF
×σ P
σM
riziková prémie (požadované převýšení bezrizikového výnosu) =
= jednotková riziková prémie × množství rizika
současná cena portfolia =
1
1
=
1 + µ P 1 + požadovaná diskontní sazba
♦
Tržní portfolio vykazuje průměrný výnos 18 % a riziko 30 %. Bezrizikový výnos činí 9 %.
Jaký výnos lze požadovat od efektivního portfolia, které je z 20 % alokováno do
bezrizikového aktiva a z 80 % do rizikového aktiva? Pro riziko portfolia platí vztah
σ P = 0,8 × σ M (poučka o kombinaci rizikového a bezrizikového aktiva). Dosazení do CML
dává
µ P = 0,09 +
0,18 − 0,09
× 0,8 × 0,3 = 16,2 %
0,3
Ke stejnému výsledku dospějeme přímo vyjádřením váženého výnosu
µ P = 0,2 × 0,09 + 0,8 × 0,18 = 16,2 %
♦
f) tržní portfolio jako stav všeobecné rovnováhy
- věta o separaci dvou fondů (two funds separation theorem): každý investor s averzí
vůči riziku (tj. se soustavou konvexních indiferenčních křivek) bude chtít
investovat do nějaké kombinace bezrizikového aktiva a tržního portfolia
(důsledek maximalizace užitku na množině investičních příležitostí)
14
Obrázek: Tržní rovnováha na trhu aktiv
Φ1 Φ 0
Φ2
µP
M
µF
σP
- jestliže se všechna individuální portfolia nalézají na přímce CML, musí se na této
přímce nalézat i agregátní portfolio všech investorů, navíc toto agregátní portfolio
musí odpovídat bodu tržního portfolia M, neboť každý jiný bod přímky CML
představuje nerovnost celkové nabídky a poptávky u bezrizikového aktiva
- v bodě M tržního portfolia dochází k rovnosti nabídky a poptávky i u všech
ostatních rizikových aktiv (existence převisů poptávky či nabídky není slučitelná
s představou celkové rovnováhy)
- v tržním portfoliu M je i-té rizikové aktivum zastoupeno vahou
θi =
tržní hodnota i - tého aktiva
tržní hodnota všech aktiv
analytický výpočet tržního portfolia
hledá se taková kombinace vah θ1 , θ 2 ,...,θ N rizikových aktiv zastoupených v
tržním portfoliu, která maximalizuje sklon spojnice bezrizikového aktiva a
rizikového tržního portfolia
N
µ − µF
Θ= P
=
σP
∑θ (µ
i =1
i
N
∑θ
i =1
i
− µF )
N
∑θ θ σ
i , j =1
za podmínky
i
i
j
→ max
ij
=1
hledanou strukturu vah lze nalézt řešením soustavy N lineárních rovnic, která
popisuje soustavu N nutných podmínek optima ∂Θ ∂θ i = 0 (důkaz Elton-
15
Gruber)
µ1 − µ F = Z 1σ 12 + Z 2σ 12 + ...... + Z N σ 1N
µ 2 − µ F = Z 1σ 12 + Z 2σ 22 + ...... + Z N σ 2 N
...............................................................
µ N − µ F = Z 1σ 1N + Z 2σ 2 N + ...... + Z N σ N2
přičemž
θi =
Zi
N
∑Z
j =1
j
3. Model oceňování kapitálových aktiv (CAPM)
model CAPM (Capital Asset Pricing Model) popisuje ekonomiku v bodě rovnováhy a
jeho základním výstupem je stanovení rovnovážného ocenění všech kapitálových
aktiv (nikoli jen efektivních portfolií ležících na přímce CML)
a) odvození přímky SML
formulace problému: Dáno je fiktivní portfolio P, které je sestaveno z a % i-tým
rizikovým aktivem a z (1 – a) % tržním portfoliem M. Jaká omezení plynou
z předpokladu, že toto portfolio je drženo v bodě tržní rovnováhy?
a) Výnos a riziko fiktivního portfolia P:
µ P = aµ i + (1 − a ) µ M
σ P = a 2σ i2 + (1 − a ) 2 σ M2 + 2a (1 − a )σ iM
b) V bodě tržní rovnováhy všichni investoři drží pouze taková portfolia, jejichž
implikovaná cena rizika je utvářena sklonem přímky CML. Stejné ocenění rizika
proto musí implikovat i fiktivní portfolio P, má-li být jeho ocenění konzistentní
s bodem tržní rovnováhy.
µi − µ M
2aσ − 2(1 − a)σ M2 + 2σ iM (1 − 2a)
dµ P dµ P da
=
=
dσ P dσ P da
2
i
− 2 2a 2σ i2 − 2(1 − a) 2 σ M2 + 2σ iM (1 − 2a)
= sklon CML =
µM − µF
σM
c) V bodě tržní rovnováhy panuje u všech aktiv (včetně i-tého aktiva) rovnost mezi
nabídkou a poptávkou. Zastoupení i-tého aktiva v tržním portfoliu M vahou θ i je
16
důsledkem této rovnováhy. Ve fiktivním portfoliu P je i-té aktivum zastoupeno
vahou θ i + a (1 − θ i ) . Pokud by váha a byla nenulová, trh i-tého aktiva by byl ve
stavu přebytečné nabídky nebo poptávky. Konzistence s tržní rovnováhou tak
vede na podmínku a = 0 . Proto
µi − µ P
µ − µF
= M
2
σM
− 2σ M + 2σ iM
− 2 σ M2
Po úpravách
µ i = µ F + (µ M − µ F )
σ iM
σ M2
= µ F + (µ M − µ F ) × β i , β i =
σ iM
σ M2
požadovaný výnos = bezrizikový výnos + cena rizika × množství rizika
= bezrizikový výnos + riziková prémie
přímka trhu cenných papírů (security market line, SML) je název odvozené lineární
závislosti mezi požadovaným výnosem rizikového aktiva a velikostí rizika měřeném
koeficientem beta (relevantním faktorem rovnovážného ocenění rizikového aktiva je
kovariance jeho výnosů s výnosem tržního portfolia)
Obrázek: Přímka trhu cenných papírů
µi
SML
µM
µF
M
F
βF = 0
βM = 1
βi
♦
Jak velký výnos je možné očekávat od zakoupení akcie, jejíž koeficient beta vykazuje
hodnotu 0,75? Bezriziková sazba je 9 % a očekávaný výnos trhu 15 %,
µ = 0,09 + (0,15 − 0,09) × 0,75 = 13,5 %
♦
17
beta vybraných aktiv:
bezrizikové aktivum: β F =
tržní portfolio: β M =
σ FM
=0
σ M2
σ MM σ M2
= 2 =1
σ M2
σM
σ EM θ M σ M2
= θM
efektivní portfolio: β E = 2 =
σM
σ M2
pro efektivní portfolia se zápis přímky SML mění na zápis přímky CML ( θ M
značí váhové zastoupení tržního portfolia v efektivním portfoliu E)
µ E = µ F + ( µ M − µ F )θ M = µ F + ( µ M − µ F )
σE
σM
obecné portfolio: beta portfolia se rovná váženému průměru bet složkových aktiv
σ PM
1
1
ri − µ i )(~
rM − µ M )] = 2 Σθ i E[(~
ri − µ i )(~
rM − µ M )]
= 2 E[ Σ θ i ( ~
2
σM σM
σM
θσ
= ∑ i 2iM = ∑ θ i β i
σM
i
i
βP =
♦
Objasnění paradoxu „neadekvátně“ oceněného rizika
Akciové portfolio
Akcie
Roční Směrodatná Beta
výnos odchylka
11 %
4%
1,1
6%
8%
0,6
Akcie má dvojnásobně vyšší riziko oproti akciovému portfoliu, přesto její roční výnos je
téměř poloviční ve srovnání s výnosem akciového portfolia. Vysvětlení paradoxu spočívá
v použití adekvátní míry rizika. Je-li uvažován koeficient beta, paradox je vysvětlen.
♦
alternativní odvození přímky SML:
- úprava nutných podmínek optima pro nalezení tržního portfolia
N
N
j =1
j =1
µ i − µ F = ∑ Z jσ ji = (ΣZ j )∑ θ jσ ji = λσ iM
využit byl fakt, že θ j zastupují váhy tržního portfolia
18
- výpočet koeficientu λ
N
N
i =1
i =1
∑θ i (µ i − µ F ) = µ M − µ F = λ ∑θ iσ iM = λσ MM = λσ M2
⇒ λ=
µM − µF
σ M2
- dosazení do výchozí rovnice
µi = µ F +
µM − µF
σ iM = µ F + ( µ M − µ F ) β i
σ M2
b) efekt diverzifikace portfolia
poznatek o významu kovariance výnosů portfolia s výnosem tržního portfolia se opírá o
efekt diverzifikace portfolia, neboli o možnost snižovat riziko portfolia pouhým
zvyšováním počtu aktiv v portfoliu
v tržní rovnováze je oceňováno pouze nediverzifikovatlené (tj. diverzifikací
neodstranitelné) riziko a nebere se ohled na diverzifikovatelné riziko, které lze
odstranit prakticky bez vynaložení nákladů
objasnění efektu diverzifikace (s následujícími předpoklady):
- stejné váhové zastoupení aktiv v portfoliu: θ i = 1 / N
- rizika všech aktiv jsou omezena nějakou společnou hodnotou: σ i2 < L
- existuje průměrná kovariance: σ =
N
σ P2 = ∑ θ i2σ i2 + 2∑ θ iθ j σ ij =
i =1
<
i< j
2∑ σ ij
i< j
N ( N − 1)
1 N 2
2
σ + 2
2∑ i
N i =1
N
∑σ
1
2 N ( N − 1)
× ( N × L) + 2 ×
×σ → σ
2
2
N
N
i< j
ij
<
pro velké N
σP
nesystematické riziko
systematické riziko
Počet akcií v portfoliu
diverzifikací neodstranitelné riziko je spojené s pohybem trhu jako celku čili s
neovlivnitelným průběhem hospodářského cyklu
19
celkové riziko = nediverzifikovatelné (systematické, tržní) riziko +
diverzifikovatelné (nesystematické, specifické, idiosynkratické, reziduální) riziko
c) zeslabování výchozích předpokladů
i) neexistence bezrizikového aktiva
Obrázek: CAPM s nulovým beta
µP
M
µZ
Z
σP
- tržní portfolio M odpovídá bodu, v němž je maximalizována směrnice přímky,
která vychází na svislé ose z bodu µ Z a která má společný bod s množinou
investičních příležitostí (není nutné, aby bod µ Z reprezentoval výnos
fyzicky existujícího bezrizikového aktiva)
- řešením soustavy nutných podmínek optima lze dospět k rovnici požadovaného
výnosu i-tého aktiva (viz alternativní odvození SML)
µ i = µ Z + (µ M − µ Z )β i , β i =
σ iM
σ M2
- odvozena tak byla rovnice modifikované přímky SML v tom smyslu, že µ Z je
prozatím pouhé číslo a nikoliv výnos reálně existujícího bezrizikového
aktiva
- všechny body množiny investičních příležitostí, které leží na přímce µ Z Z ,
odpovídají reálně existujícím rizikovým aktivům s výnosem µ Z , mezi
všemi těmito body má nejnižší riziko hraniční aktivum Z
- modifikovaná přímka SML se vztahuje na všechna aktiva či portfolia aktiv, tedy
i na aktivum Z, neboli
µ Z = µ Z + (µ M − µ Z )β Z
⇒ βZ = 0
20
aktivum Z (stejně jako všechny ostatní body přímky µ Z Z ) má nulové beta
(není korelováno s tržním portfoliem)
- při absenci bezrizikového aktiva platí vtah SML v modifikované podobě, kdy
výnos bezrizikového aktiva je nahrazen výnosem hraničního aktiva
s nulovým beta
- Rollova kritika
při odvození přímky SML nehrálo tržná portfolio žádnou specifickou roli,
stejnou proceduru lze použít pro každý efektivní bod E hranice investičních
příležitostí a výsledkem bude odvození modifikované přímky SML
µ iE = µ ZE + ( µ E − µ ZE ) β iE , β i =
σ iE
σ E2
důsledek: empirické aplikace nepracují s tržním portfoliem, které je
nepozorovatelné, nýbrž používají nějakou jeho aproximaci
⇒ testování platnosti modelu CAPM je tedy pouze testováním toho, zda
jako náhražka tržního portfolia bylo použito efektivní portfolio
⇒ je obtížné vyslovovat soudy o podhodnocených či nadhodnocených
aktivech, jestliže nepracujeme s pravou SML nýbrž pouze s jednou
z jejích empirických náhražek
obrana: Rollova kritika nepopírá platnost samotného modelu, pouze je skeptická
vůči schopnosti ekonometrických technik tuto platnost verifikovat
ii) rozdílná výpůjční a zápůjční bezriziková sazba
lineární průběh CML se opírá o předpoklad existence bezrizikové sazby, za níž
lze v neomezené míře zapůjčovat a vypůjčovat peněžní prostředky
pro praxi je ale typická odlišná hladina výpůjční a zápůjční sazby (vypůjčované
fondy bývají dražší než zapůjčované) a obvykle si nelze vypůjčovat
v neomezeném množství (předpoklad neomezeného zapůjčování již není tak
restriktivní)
tři úseky efektivní hranice:
1. investoři, kteří kupující bezrizikové aktivum (zapůjčují peníze za sazbu
µ FL ), volí body na přímce µ FL L (nalevo od bodu L), přičemž
21
µ P = µ FL + ( µ L − µ FL )
σ PL
σ L2
2. investoři, kteří provádějí krátký prodej bezrizikového aktiva (vypůjčující
si peníze za sazbu µ FB , volí body na přímce µ FB B (napravo od bodu B),
přičemž
µ P = µ FB + ( µ B − µ FB )
σ PB
σ B2
3. investoři, kteří investují pouze do rizikových aktiv, volí hraniční portfolia
v úseku LB, přičemž
µ P = µ Z + (µ M − µ Z )
σ PM
σ M2
Obrázek: Efektivní hranice při rozdílné výpůjční a zápůjční sazbě
µP
µ FB
µ FL
L
M
B
Z
σP
důsledky: - existuje mnoho kandidátů na tržní portfolio (v principu to může být
jakýkoli bod hraničního úseku LB )
- tržní portfolio si podržuje vlastnost efektivního portfolia, jelikož je
tvořeno složkami (L,M,B), jež reprezentují rovněž efektivní
portfolia
iii) heterogenní očekávání
standardní CAPM pracuje s předpokladem homogenních očekávání, podle něhož
všichni investoři mají stejný názor na rizikovost a výnosnost aktiv
(konfrontováni jsou stejnou množinou investičních příležitostní)
předpoklad heterogenních očekávání (tj. různě vnímaných množin investičních
příležitostí) výrazně komplikuje modelové výsledky
iv) další směry zobecňování CAPM
22
- existence neobchodovaných aktiv
- zahrnutí daní
- CAPM orientovaný na spotřebu (vliv korelace očekávaných výnosů aktiv
s růstem spotřeby na hlavu)
- rozšíření na větší počet období
- existence investorů schopných ovlivňovat ceny aktiv
4. Jednoindexní model
CAPM je z rodiny modelů všeobecné rovnováhy, které popisují ekonomiku ve stavu
rovnosti nabídky a poptávky na všech trzích jako výsledek úsilí jednotlivců o
maximalizaci svého užitku. Základní vlastností rovnovážného stavu dle CAPM je
oceňování rizikových aktiv podle velikosti korelace výnosů aktiv s pohybem tržního
indexu.
Jednoindexní model (single-index model) je z rodiny ekonometrických přístupů
k oceňování rizikových aktiv, jenž vychází z předpokladu, že existuje jediný
společný faktor vysvětlující fundamentální cenový pohyb aktiv, přičemž všechny
ostatní cenové vlivy lze podřadit pod působení nahodilých výkyvů
a) odvození základních vztahů
výnos rizikového aktiva je fundamentálně svázán s výnosem tržního indexu a
současně podléhá působení náhodných vlivů (charakteristická přímka i-tého aktiva)
~
~
Ri = ci + β i RM + ε~i
~
Ri … očekávaný výnos i-tého rizikového aktiva
~
RM … očekávaný výnos tržního indexu jako společný fundamentální
faktor oceňování aktiv
β i … citlivost ceny i-tého aktiva na pohyb tržního indexu
ci … fixní složka reziduálního výnosu i-tého aktiva
ε~i …náhodná složka reziduálního výnosu
vlastnosti náhodného členu
~
E (ε~i ) = 0, E (ε i ) 2 = η i2 , cov(ε~i , RM ) = 0, cov(ε~i , ε~ j ) = 0
výnos a riziko individuálního aktiva:
23
~
~
µ i = E (ci + β i RM + ε~i ) = E (ci ) + E ( β i RM ) + E (ε~ )
= ci + β i µ M
~
~
σ i2 = E[(ci + β i RM + ε~i ) − (ci + β i µ M )]2 = E[ β i ( RM − µ M ) + ε~i ]2
~
~
= β i2 E ( RM − µ M ) 2 + 2β i E[( RM − µ M )ε~i ] + E (ε i ) 2
= β i2σ M2 + η i2
~
~
~
~
σ ij = E[( Ri − µ i )( R j − µ j )] = E[( β i ( RM − µ M ) + ε~i )( β j ( RM − µ M ) + ε~ j )]
= β i β j σ M2
výnos a riziko portfolia aktiva:
N
N
N
~
~
~ N
~
R P = ∑ θ i Ri = ∑ θ i ci + RM ∑ θ i β i + ∑ θ i ε~i = c P + β P RM + ε~P
i =1
i =1
i =1
N
M
i =1
i =1
i =1
µ P = ∑ θ i ci + µ M ∑ θ i β i = c P + β P µ M
N
σ P2 = ∑ θ i2σ i2 + 2∑ θ iθ j σ ij
i =1
i< j
N
N
= σ M2 ∑ θ i2 β i2 + 2σ M2 ∑ θ iθ j β i β j + ∑ θ i2η ε2i =
i =1
=β σ
2
P
2
M
i< j
+η
i =1
2
P
(rozklad celkového rizika na systematickou a nesystematickou část)
srovnání nároků na počet odhadovaných parametrů:
variančně-kovarianční přístup: N variancí σ i2 +
1
2
N ( N − 1) kovariancí σ ij
50 akcií ⇒ 1275 odhadů, 200 akcií ⇒ 20100 odhadů
jednoindexní model: N koeficientů β + N reziduálních rizik η i + riziko trhu σ M
50 akcií ⇒ 101 odhadů, 200 akcií ⇒ 401 odhadů
b) odhady koeficientů beta
i) odhady historického beta lineární regresí
standardní regresní analýza metodou nejmenších čtverců
Ri ,t = ci + β i RM ,t + ε t ,
∑ (R
i ,t
− µ i ) 2 → min
výpočetní tvar parametrů regresní přímky má shodné rysy s CAPM
βi =
σ iM
, ci = µ i − β i µ M
σ M2
♦
24
Proveďte rozklad celkového rizika i-tého aktiva na diverzifikovatelnou a
nediverzifikovatelnou složku, činí-li celkové riziko aktiva 35 %, riziko tržního portfolia je 25
% a kovariance aktiva s trhem je 0,053.
2
σ iM
0,053 2
systematická složka rizika = β σ = 4 × σ M2 =
= 0,045
σM
0,25 2
2
i
2
i
nesystematická složka rizika = 0,35 2 − 0,045 = 0,077
Z celkového rizika tvoří 37 % nediverzifikovatelnou část ( = 0,045 / 0,35 2 ), zbylých 67 %
připadá na diverzifikovatlnou část. (Rozklad lze provádět pro druhé mocniny rizika).
♦
ii) odhady fundamentálního beta
regresní analýzy objasňující velikost koeficientů beta vybranými fundamentálními
charakteristikami firmy (dividendový výnos, objem a dynamika růstu aktiv,
zadluženost, …) a využívání prognóz firemních charakteristik k prognózování
beta
problémový předpoklad o neměnné citlivosti beta vůči fundamentálním
charakteristikám
5. Teorie arbitrážového oceňování
model APT (Arbitrage Pricing Theory) rozpracovává přístup k tvorbě cen aktiv na bázi
arbitrážového principu: portfolio, které ke svému sestavení nevyžaduje vynaložení
nákladů a nevykazuje žádné riziko, musí mít nulový očekávaný výnos
model postuluje závislost očekávaného výnosu rizikového aktiva na větším počtu
společných fundamentálních faktorů jako zdroje systematického rizika
~
~
~
Ri = µ i + bi1 F1 + K + biK FK + ε i
~
Fk ... k-tý faktor působící na výnosy rizikových aktiv (k = 1, …, K)
~
dle konstrukce modelu E ( Fk ) = 0
bik … citlivost i-tého aktiva na velikost k-tého faktoru (i = 1,…,N; k =
1,…,K)
µ i … konstantní složka reziduálního výnosu
ε~i … náhodná složka reziduálního výnosu, náhodný šum i-tého aktiva
~
dle předpokladu E (ε~i ) = 0, cov(ε~i , Fk ) = 0, cov(ε~i , ε~ j )
25
i) odvození základní formule
- provedeno je přeskupení portfolia, které nevyžaduje dodatečné nároky na zdroje
( δ i značí změnu váhy zastoupení i-tého aktiva v portfoliu)
N
∑δ
i =1
i
=0
N
N
N
N
N
~
~
~
~
∆R P = ∑ δ i Ri = ∑ δ i µ i + ∑ δ i bi1 F1 + K + ∑ δ i biK FK + ∑ δ i ε i
i =1
i =1
i =1
i =1
i =1
- od uvedeného přeskupení je navíc vyžadována podmínka, aby do portfolia
nebylo vnášeno žádné dodatečné riziko
nesystematické riziko lze odstranit diverzifikací čili velkým počtem aktiv
v portfoliu (pro jednoduchost volíme přibližně stejnou proporcionální
změnou v zastoupení aktiv
δi ≈ ±
1
N
⇒
N
∑ δ i ε~i ≈
i =1
1
N
N
∑ ± ε~
i =1
i
→ 0 pro velké N
systematické riziko lze odstranit splněním K omezujících podmínek (při
mnohonásobně vyšším počtu aktiv než faktorů systém disponuje
dostatečnou flexibilitou)
∑δ b
i i1
i
= 0, K , ∑ δ i biK = 0
i
- s přihlédnutím k uvedeným omezujícím podmínkám pro změnu portfolia
vychází
N
~
∆R P = ∑ δ i µ i
i =1
- provedeno bylo přeskupení portfolia, která naplňuje oba předpoklady
arbitrážového principu (nulové náklady, nevnášení rizika), proto i
očekávaný výnos této změny musí být nulový
N
∆µ P = ∑ δ i µ i = 0
i =1
- věta lineární algebry: Je-li vektor δ = (δ 1 , Kδ N ) kolmý na jednotkový vektor
(Σδ i .1 = 0) a na vektory bk (Σδ i bik = 0) , pak vektor očekávaných
výnosů ( µ1 , K , µ N ) , který je rovně kolmý na vektor δ (Σδ i µ i = 0) , musí
ležet v prostoru generovaném jednotkovým vektorem a vektory bk .
Neboli existují konstanty λ0 , λ1 , K λ K takové, že platí vektorová rovnice
26
( µ1 , K , µ N ) = λ0 (1, K ,1) + λ1 (b11 , K , bN 1 ) + K + λ K (bN 1 , K , bNK )
Rozepsání této rovnice po jednotlivých složkách dává
µ i = λ0 + λ1bi1 + K + λ K biK , i = 1,..., N
- závěrečné úpravy
existuje-li bezrizikové aktivum (s nulovými citlivostmi vůči všem
společným faktorům), bude
λ0 = µ F
parametr λ k lze modifikovat do podoby „rizikové přirážky“ za závislost na
systematickém riziku generovaném k-tým faktorem (parametr γ k značí
očekávaný výnos portfolia s jednotkovou citlivostí vůči k-tému faktoru a
nulovou citlivostí vůči všem ostatním faktorům)
λk = γ k − µ F
- finální výstup modelu APT
µ i = µ F + (γ i1 − µ F )bi1 + K + (γ iK − µ F )biK
ii) empirické odhady APT
~
1. krok: identifikace společných faktorů Fk a odhad citlivostí bik
postup: vytipování faktorů (inflace, dividendový výnos, velikost firmy, …)
a odhad citlivostí standardními technikami regresní analýzy
faktorová analýza spočívající ve vyhledání optimálního počtu
faktorů s požadovanou vysvětlovací silou
2. krok: aplikace technik regresní analýzy pro odhad koeficientů λ k
postup: jako vysvětlující proměnné mohou být použity buď již provedené
odhady citlivostí výnosů vůči společným faktorům a nebo přímo
naměřené hodnoty společných faktorů
iii) víceindexní model (multi-index model)
ekonometrický přístup pro determinaci očekávaných výnosů aktiv, který se
neopírá o prvky rovnovážného uvažování
odhadována je regresní závislost
~
~
~
Ri = µ i + β i1 I 1 + K + β iK I K + ε i
dle konstrukce modelu:
~ ~
E (ε i ) = 0, cov( Fi , F j ) = 0 (provedení tzv. ortogonalizace indexů)
27
dle předpokladu modelu:
cov(ε i , ε j ) = 0
příklady indexů: hospodářský růst, pozice v hospodářském cyklu, dlouhodobé a
krátkodobé úrokové sazby, inflace, kurz
28
B. ŘÍZENÍ PORTFOLIA
1. Základní pojmy
obsah řízení portfolia (pracovní náplň portfolio manažera):
- sestavení portfolia (investování peněžních prostředků v souladu s preferencemi
investujících klientů)
- analýza portfolia (měření a vyhodnocování výkonnosti portfolia, identifikace
investičních rizik, provádění srovnávacích analýz)
- upravování portfolia (provádění obchodů se složkovými aktivy portfolia s ohledem
na měnící se okolnosti)
základní typologie klientů:
- brutto investor (gross investor)
investor umisťující vlastní prostředky do portfolia, které odpovídá jeho
rizikovému profilu (preferencím mezi výnosem a rizikem)
- netto investor (net investor)
investor požadující sestavení takového portfolia, které by ze svých výnosů
průběžně pokrývalo nabíhající závazky (penzijní fond, podnikový finanční
manažer, aj.)
základní typologie technik řízení:
- pasivní řízení portfolia
vyznačuje se méně významnými a méně častými úpravami portfolia
opora v představě efektivně fungujících trhů, které vesměs korektně oceňují
obchodovaná aktiva a proto poskytují malý prostor vydělávat na cenových
distorzích a systematicky překonat výkon trhu
- aktivní řízení portfolia
vyznačuje se častými a podstatnými úpravami portfolia
představa poměrně častých a významných cenových distorzí, jejichž
identifikací na základě lepších znalostí a informací lze vydělávat
abnormální výnosy (analýza očekávaného pohybu úrokových sazeb,
měnových kurzů, ratingového hodnocení, výnosových spreadů, aj.)
hypotéza efektivních trhů (efficient market hypothesis, EMH)
- slabá forma EMH:
29
aktuální ceny cenných papírů okamžitě a plně odrážejí veškerou minulou
informaci a neposkytují žádné vodítko k budoucímu chování cen
obchody založené na analýze historických cen neumožňují vydělávat abnormální
zisky
- polosilná forma EMH:
aktuální ceny cenných papírů okamžitě a plně odrážejí veškeré dostupné
informace
neexistují významnější zpoždění mezi zveřejněním informací a jejich
zakomponováním do cen
- silná forma EMH:
aktuální ceny cenných papírů plně a okamžitě odrážejí veškerou známou
informaci včetně neveřejných důvěrných informací)
složky tržní efektivnosti jsou alokační efektivnost, operační efektivnost a informační
efektivnost
2. Techniky pasivního řízení portfolia
a) užitková funkce brutto investora
maximalizace hodnoty portfolia při respektování rizikového profilu klienta
i) strategie „kup a drž“ (buy-and-hold strategy)
aktiva bez stanovené doby splatnosti (akcie) jsou trvale držena v portfoliu a aktiva se
stanovenou splatností (obligace, instrumenty peněžního trhu) jsou při splatnosti
nahrazována stejnými aktivy
výnos portfolia je založen na důchodovém toku cenných papírů (kupónové platby,
dividendy, trendové zhodnocování), ke krátkodobým kapitálovým ziskům a
ztrátám se nepřihlíží
ii) sledování indexu (index matching, index tracking)
sestavené portfolio je zmenšenou kopií určitého referenčního indexu (benchmark)
výkonnost portfolia je srovnávána s výkonností referenčního portfolia a
vyhodnocována je sledovací chyba (tracking error)
- kompletní indexování
konstrukce řízeného portfolia věrně kopíruje složení sledovaného portfolia
nevýhodou je nákladné upravování (rebalancování) portfolia
30
zdroje sledovací chyby:
- transakční náklady související se sledováním struktury indexu (vyřazování a
zařazování akcií, končící splatnost obligací, existence obchodního rozpětí se
silným vlivem likvidity příslušného trhu, aj.)
- obtížné sledování hotovostního toku indexu (hotovostní tok řízeného portfolia
podléhá zdanění, reinvestování výnosů je spojeno s transakčními náklady,
existuje prodleva mezi deklarací a výplatou dividend či kupónů, aj.)
- vzorkování (sampling)
rozdělení všech aktiv indexu do sektorů a buněk podle vytipovaných
charakteristik a výběr představitelů každé buňky v souladu s váhou daného
sektoru na sledovaném indexu
♦
Příklad vzorkování obligačního portfolia
1. Splatnost obligace
a) méně než 5 let
b) mezi 5 a 10 lety
c) větší než 10 let
2. Tržní sektor
a) vládní obligace
b) korporace
c) agentury
3. Rating
a) AAA
b) AA
c) A
d) BBB
Celkem bylo vytvořeno 3 × 3 × 4 = 36 buněk. Jestliže např. ve sledovaném indexu je
zastoupeno 23 % agenturních obligací se splatností větší než 10 let a s ratingem AA, stejné
váhové zastoupení daného segmentu by mělo vykazovat i sestavené portfolio.
♦
aplikace optimalizačních technik a dodatkových omezení při vytváření vzorku (prvky
aktivního řízení):
31
- maximalizace výnosu do splatnosti
- minimalizace sledovací chyby
- vědomé podvažování či nadvažování vybraných sektorů
- limity na zastoupení vybraných sektorů
iii) posílené indexování
prvek aktivního řízení v rámci celkově pasivního přístupu k řízení portfolia
vědomé podstupování mírného dodatečného rizika s cílem dosáhnout lepší
výkonnosti oproti referenčnímu indexu (zařazování výnosnějších titulů,
techniky syntetického vytváření aktiv, aj.)
b) užitková funkce netto investora
formování a řízení portfolia s cílem uspokojovat danou strukturu závazků
i) imunizace obligačního portfolia
zajišťování hodnoty obligačního portfolia proti změnám úrokových sazeb
pravidlo imunizace: 1. závazek splatný v budoucím okamžiku T jistit investicí do
obligačního portfolia s durací T
2. velikost jistícího obligačního portfolia stanovit ve výši současné
hodnoty budoucího závazku
3. periodické upravování obligačního portfolia obnovující
imunizační pravidlo
♦
Manažer penzijního fondu emitoval obligace v nominální hodnotě 8 820 262 $, které po dobu
5,5 let garantují šestiměsíční výnos 6,25 % (tj. 12,5 % ročně). Garantovaný závazek vůči
držitelům obligací splatný po uplynutí 5,5 let tak činí
8 820 262 × (1 + 0,0625)11 = 17 183 032 $
1) Zakoupení pari obligace v nominální hodnotě 8 820 262 $, s ročním kupónem 12,5 %
(vypláceným pololetně) a se splatností 5,5 let.
Úroková
sazba
Reinvestovan
ý
kupón
Cena
obligace
Akumulovaná
hodnota
Efektivní
výnos
Diference
32
1
2
3
4
5
14,0
8700967
8820262
17521230
12,88
338198
12,5
8362770
8820262
17183032
12,50
0
11,0
8039392
8820262
16859654
12,13
-323378
⎛ {1} ⎞
{2} = ∑ 8 820 262 × 0,0625 × ⎜1 +
⎟
2 ⎠
⎝
t =1
11
6
11− t
{4} = {2} + {3}
{5} = 2 ×
( {4} 8 820 262 − 1)
11
{6} = {4} − 17 183 032
2) Zakoupení pari obligace 8 820 262 $, s ročním kupónem 12,5 % (vypláceným pololetně) a
se splatností 15 let. V okamžiku plnění závazku obligaci zbývá do splatnosti 9,5 roku.
1
Reinvestovan
ý
kupón
2
14,0
8700967
8136542
16837510
12,11
-345522
12,5
8362770
8820262
17183032
12,50
0
11,0
8039392
9322113
17627523
12,99
-444491
Úroková
sazba
Cena
obligace
Akumulovaná
hodnota
Efektivní
výnos
Diference
3
4
5
6
11
⎛ {1} ⎞
{2} = ∑ 8 820 262 × 0,0625 × ⎜1 +
⎟
2 ⎠
⎝
t =1
8 820 262 × 0,0625
19
{3} = ∑
⎛ {1} ⎞
⎜1 + ⎟
2 ⎠
⎝
t =1
t
+
11− t
8 820 262
⎛ {1} ⎞
⎜1 + ⎟
2 ⎠
⎝
19
{4} = {2} + {3}
{5} = 2 ×
( {4} 8 820 262 − 1)
11
{6} = {4} − 17 183 032
3) Zakoupení pari obligace 8 820 262 $, s ročním kupónem 12,5 % (vypláceným pololetně),
které zbývá půl roku do splatnosti, a reinvestování šestiměsíčního výnosu do 5lého
termínového depozita.
Úroková
sazba
Příjem za
6 měsíců
Akumulovaná
hodnota
Efektivní
výnos
Diference
33
1
2
3
4
5
14,0
9371528
18435215
13,86
1252183
12,5
9371528
17183032
12,50
0
11,0
9371528
16007924
11,14
-1175108
⎛ 0,125 ⎞
{2} = 8 820 262 × ⎜1 +
⎟
2 ⎠
⎝
⎛ {1} ⎞
{3} = 9 371 528 × ⎜1 +
⎟
2 ⎠
⎝
10
(
)
{4} = 2 × 11 {3} 8 820 262 − 1
{5} = {3} − 17 183 032
4) Zakoupení 8-leté obligace s ročním kupónem 10,125 % za cenu 88,202 (na 100 nominále).
Obligace vykazuje výnos do splatnosti 12,5 % a duraci v délce horizontu závazku,
D=
100 ⎛ 16
0,10125 / 2
1
⎜⎜ ∑ t ×
+ 16 ×
t
88,202 ⎝ t =1 (1 + 0,125 / 2)
(1 + 0,125 / 2)16
⎞
⎟⎟ = 11 měsíců = 5,5 let
⎠
1
Reinvestovan
ý
kupón
2
14,0
7990447
9205587
17196034
12,51
13002
12,5
7679867
9503166
17183032
12,50
0
11,0
7382896
9813175
17196071
12,51
13039
Úroková
sazba
Cena
obligace
Akumulovaná
hodnota
Efektivní
výnos
Diference
3
4
5
6
Postup výpočtu údajů tabulky je shodný s případem č. 2.
praktické problémy imunizace:
- větší pohyby úrokových sazeb snižují kvalitu imunizace (durace je mírou
cenového rizika pouze prvního řádu)
- přirozené stárnutí obligací snižuje duraci obligačního portfolia pomaleji ve
srovnání se zkracováním splatnosti závazku
- nutnost ošetřování dalších rizik (kreditní riziko, riziko přivolání, aj.) zvyšuje
transakční náklady na udržování imunizovaného portfolia, zaměření
pouze na vládní obligace generuje minimální výnos
- častá frekvence upravování portfolia zvyšuje transakční náklady, nízká
34
frekvence snižuje kvalitu imunizace
- při neparalelním posunu výnosové křivky vzniká imunizační riziko (porušen
je základní předpoklad pro vypovídací schopnost durace jako míry
tržního rizika)
zajišťování imunizačního rizika:
soustředné portfolio (focused, bullet p.) je tvořeno obligacemi, jejichž durace se
nacházejí poblíž durace závazku, přičemž vážená durace portfolia se rovná
duraci závazku
odstředné portfolio (barbell p.) je tvořeno obligacemi, jejichž durace se nachází
dále od durace závazku, přičemž vážená durace portfolia se rovná duraci
závazku
♦
K dispozici jsou obligace s duracemi 4, 9, 11 a 14 let. Soustředné portfolio o duraci 10 let lze
sestavit s 50 %-ním zastoupením obligací o duranci 9 a 11 let,
0,5 × 9 + 0,5 × 11 = 10 let
Odstředné portfolio o duraci 10 let lze sestavit při 40 %-ním resp. 60 -%ním zastoupením
obligací o duraci 4 resp. 14 let,
0,4 × 4 + 0,6 × 14 = 10 let
♦
při paralelním posunu výnosové křivky jsou soustředná i odstředná portfolia stejně
výhodná
při neparalelním posunu je imunizačním rizikem více zatíženo odstředné portfolio
(např. při poklesu krátkého konce a nárůstu dlouhého konce výnosové křivky má
odstředné portfolio větší ztrátu z reinvestovaného i kapitálového výnosu)
vícečasová imunizace (multi-period immunisation)
technika jištění časové struktury závazků (nikoli jen jednoho závazku v jediném
budoucím okamžiku) proti změnám úrokových sazeb
nutná taková dekompozice hotovostního toku obligačního portfolia, která by
imunizovala každý jednotlivý závazek
ii) párování hotovostních toků (cash flow matching)
35
metoda párování spočívá v sestavení portfolia obligací (tzv. dedikovaného portfolia),
jejichž hotovostní tok (platby kupónu a jistiny) vykrývá zadanou časovou
strukturu závazků
vykrývání závazků postupuje od konce horizontu k jeho počátku
párovací schéma:
krok 0 : - zadána je výchozí T-letá struktura závazků L10 , L02 , K, L0T
- k dispozici je T-letá obligace A s hotovostním tokem A1 , A2 , K, AT
- zakoupeno je n A kusů obligace A za účelem vykrytí posledního závazku,
n A AT = L0T
krok 1: - zůstává nekrytá struktura závazků L11 = L10 − n A A1 , K , L1T −1 = L0T −1 − n A AT −1
- použita je (T-1)-letá obligace s hotovostním tokem B1 , B2 ,K, BT −1
- zakoupeno je n B kusů obligace B pro vykrytí předposledního závazku
n B BT −1 = L1T −1
krok 2: - zůstává nekrytá struktura závazků L12 = L11 − n B B1 , K , L2T − 2 = L1T − 2 − n B BT − 2
- použita je (T-2)-letá obligace s hotovostním tokem C1 , C 2 ,K, CT −2
- zakoupeno je nC kusů obligace C pro vykrytí předpředposledního závazku
nC CT − 2 = L2T − 2
algoritmus pokračuje uvedeným způsobem až do úplného vypárování všech závazků
hotovostním tokem portfolia obligací
♦
Penzijní fond bude během následujících tří let každý rok vyplácet svým klientům 1000 mil.
USD. K dispozici jsou následující obligace
Splatnost
Kupón
Nominále
A
3
11,1
100
B
2
12,5
100
C
1
14,3
100
Způsob vypárování zadané struktury závazků
36
Rok
Závazek
9 obligací A 8 obligací B
1
1000
100
100
2
1000
100
900
3
1000
1000
7 obligací C
800
L3 = 1000 = 9 × (11,1 + 100)
L2 = 1000 = 9 × 11,1 + 8 × (12,5 + 100)
L1 = 1000 = 9 × 11,1 + 8 × 12,5 + 7 × (14,3 + 100)
♦
výhody: - obligační portfolio není vystaveno tržnímu riziku, neboť všechny obligace jsou
drženy do splatnosti
- není nutné provádět úpravy portfolia (s výjimkou ošetřování kreditního rizika)
nevýhody: často nákladná strategie z důvodu nemožnosti dokonale vykrýt závazky
existujícími obligacemi, což ústí do určitého předimenzování dedikovaného
portfolia
iii) podmíněná imunizace
vytvoření prostoru pro aktivní řízení obligačního portfolia za podmínky, že hodnota
portfolia neklesne pod mez stanovenou tzv. bezpečnostním polštářem
je-li bezpečnostní polštář vyčerpán, řízení portfolia přechází do režimu imunizace
♦
Aktuální 4-letý tržní výnos do splatnosti činí 12 %. Klient investující 50 mil USD na čtyři
roky je ochoten akceptovat bezpečnostní polštář 200 b.p. pod aktuálním tržním výnosem.
Jinými slovy souhlasí s aktivním řízením portfolia za podmínky, že dosažen bude minimální
výnos 10 %, čemuž odpovídá cílová hodnota portfolia
50 000 000 × (1 + 0,05) 8 = 73 872 772 USD
V nominálním vyjádření byl tak manažerovi vytvořen bezpečnostní polštář ve výši
50 000 000 −
73 872 772
= 50 000 000 − 46 348 691 = 3 651309 USD
(1 + 0,06) 8
Manažer očekává pokles úrokových sazeb, a proto investuje svěřených 50 mil USD do
nákupu 20leté pari obligaci s kupónem 12 %, namísto zakoupení obligace s durací 4 roky,
která by zajistila výnos 12 % proti pohybu úrokových sazeb
37
a) po uplynutí 6 měsíců úrokové sazby klesly z 12 % na 9 %
39
nová cena obligace =
6
∑ (1 + 0,045)
t =1
t
+
100
= 127,34
(1 + 0,045) 39
vyplacený kupón = 50 000 000 × 0,06 = 3 000 000
nová hodnota portfolia = 3 000 000 + 50 000 000 ×
investice potřebná k dosažení cílové částky =
127,34
= 66 670 000
100
73 872 772
= 54 283 815
(1 + 0,045) 7
bezpečnostní limit = 66 670 000 − 54 283 815 = 12 386 112
Bezpečnostní limit v peněžním vyjádření byl úspěšným řízením portfolia zvýšen, což
umožňuje dále pokračovat v aktivním řízení.
b) po uplynutí 6 měsíců úrokové sazby vzrostly ze 12 % na 14 %
39
nová cena obligace =
6
∑ (1 + 0,07)
t =1
t
+
100
= 86,74
(1 + 0,07) 39
vyplacený kupón = 50 000 000 × 0,06 = 3 000 000
nová hodnota portfolia = 3 000 000 + 50 000 000 ×
investice potřebná k dosažení cílové částky =
86,74
= 43 370 000
100
73 872 772
= 46 004 250
(1 + 0,07) 7
bezpečnostní limit = 43 370 000 − 46 004 250 = −2 634 250
Bezpečnostní polštář byl přečerpán, takže manažer je povinen imunizovat portfolio čili
zakoupit obligaci s durací 3,5 let a s minimálním výnosem 14 %, která umožní zajistit
zaručenou cílovou částku proti změnám úrokových sazeb.
♦
3. Techniky aktivního řízení portfolia
snaha těžit z očekávaných pohybů cen cenných papírů (odstraňování dočasných
cenových anomálií, očekávaný příchod nových informací, formování vlastního
názoru na výnosnost a rizikovost aktiv, aj. )
rozhodovací úrovně: - základní kategorie
volba mezi základními třídami aktiv, která předurčuje rizikový
profil portfolia a jeho výkonnost (základní členění na akcie,
obligace a nástroje peněžního trhu)
38
- sektory
jsou širší třídy aktiv v rámci základních kategorií
(akcie: banky, elektronika, pivovary, textilky, aj.)
- cenné papíry
výběr zcela konkrétních titulů v souladu s použitými technikami
aktivního řízení
a) aktivní řízení akciového portfolia
i) vyhledávání pozitivního alfa (quest for alpha)
koeficient alfa měří přebytečný výnos akcie definovaný jako rozdíl mezi fakticky
pozorovaným výnosem akcie a fundamentálním (modelově-teoretickým) výnosem akcie
(např. dle modelu CAPM)
α > 0 ⇒ akcie je podhodnocená (akcie má pozitivní alfa)
akcie vykazuje vyšší výnos (nižší cenu) než jaký by odůvodňovala
fundamentální analýza
signál k nákupu akcie, neboť lze očekávat růst ceny akcie a tím i
snižování jejího výnosu směrem k teoretické hodnotě
α < 0 ⇒ akcie je nadhodnocená (akcie má negativní alfa)
akcie vykazuje nižší výnos (vyšší cenu) než jaký by odůvodňovala
fundamentální analýza
signál k prodeji akcie (popř. k „šortování“ akcie), neboť lze
očekávat pokles ceny akcie a tím i zvyšování jejího výnosu
směrem k teoretické hodnotě
Obrázek: Akcie s pozitivním a negativním alfa
µi
• A1
SML
α1
µF
α2
A2 •
βi
A1 je podhodnocená akcie (pozitivní α)
A2 je nadhodnocená akcie (negativní α)
39
alfa portfolia se získá jako vážený součet koeficientů alfa individuálních akcií v
portfoliu
N
α P = ∑ θ iα i
i =1
θ iP … váha i-té akcie v portfoliu P
cílem strategie vyhledávání alfa je snaha o nadproporcionální zastoupení
podhodnocených akcií (akcií s kladným alfa) a podporoporcionální zastoupení
nadhodnocených akcií (akcií se záporným alfa) oproti tržnímu portfoliu
N
α P = ∑ (θ iM + δ i )α i
i =1
θ iM … váha i-té akcie v tržím portfoliu
δ i … „sázka“ na i-tou akcii (může být kladné i záporné
číslo)
ii) selekce akcií dle přebytečného výnosu k beta (Elton-Gruber)
přebytečný výnos k beta =
µi − µ F
βi
(převýšení bezrizikového výnosu vztažené na jednotku systematického
rizika)
algoritmus: 1. sestupné seřazení akcií dle přebytečného výnosu k beta (od nejvyššího
k nejnižšímu)
2. výpočet dělícího bodu pro portfolio sestavené z n nejlepších akcií (dle
přebytečného výnosu k beta)
3. pokud je přebytečný výnos (n+1)-ní akcie vyšší než hodnota dělícího
bodu, o tuto akcii bude portfolio rozšířeno
4. výpočet dělícího bodu pro portfolio sestavené z (n+1) nejlepších akcií a
dále v logice bodu 3
cj =
j
⎡
i =1
⎣
σ M2 ∑ ⎢(µ i − µ F )
βi
2
i =1 η i
βi ⎤
⎥
η i2 ⎦
j
1 + σ M2 ∑
, θi =
Zi
, Zi =
N
∑Z
j =1
j
βi
η i2
⎛ µi − µ F
⎞
⎜⎜
− cˆ ⎟⎟
⎝ βi
⎠
c j … dělící bod vypočítaný z vlastností prvních j akcií
)
c … výsledný dělící bod
40
N … počet akcií ve výsledném portfoliu
♦
Přebytečn
ý
výnos
10,0
Dělící
bod
1,0
Specifick
é
riziko
50
17
1,5
40
8,0
3,69
3
12
1,0
20
7,0
4,42
4
17
2,0
10
6,0
5,43
5
11
1,0
40
6,0
5,45
6
11
1,5
30
4,0
5,30
7
11
2,0
40
3,0
5,02
8
7
1,8
16
2,5
4,91
9
7
1,0
20
2,0
4,75
Akcie
Očekávaný
výnos
Beta
akcie
1
15
2
1,67
♦
iii) časování trhu (market timing)
techniky aktivního řízení vyvolané odlišným pohledem na očekávanou výkonnost
tržního portfolia (společné působení hospodářského cyklu na všechny akcie)
býčí očekávání … manažer se domnívá, že trh podhodnocuje očekávanou výkonnost
tržního portfolia ⇒ aplikace technik zvyšujících beta řízeného portfolia
medvědí očekávání … manažer se domnívá, že trh nadhodnocuje očekávanou
výkonnost tržního portfolia ⇒ aplikace technik snižujících beta řízeného
portfolia
techniky uzpůsobování beta:
- nákup resp. prodej akcií v souladu s jejich beta
agresivní akcie má koeficient beta vyšší než 1
držením těchto akcií je podstupováno více nediverzifikovatelného
rizika, očekávaný výnos by měl být proto relativně vyšší
při býčím trhu tato akcie roste více než trh a při medvědím trhu klesá
více než trh
defenzivní akcie má koeficient beta nižší než jedna
držením této akcie je podstupováno méně nediverzifikovatelného
41
rizika, očekávaný výnos by měl být proto relativně nižší
při býčím trhu tato akcie roste méně než trh a při medvědím trhu klesá
méně než trh
- prodlužování či zkracování beta portfolia s využitím futuritních a opčních
kontraktů
iv) pojišťování portfolia (portfolio insurance)
investiční strategie imitující ochrannou prodejní opci (zakoupení prodejní opce
k dané akcii ponechává ziskový potenciál při růstu ceny akcie a limituje ztrátu při
poklesu ceny akcie)
dynamická alokace mezi akciemi a obligacemi (programové obchodování)
při býčím trhu dochází k přeskupování portfolia ve prospěch rizikových akcií, při
medvědím trhu je portfolio naopak přeskupováno ve prospěch bezpečných
obligací
♦
Akciové portfolio má aktuální hodnotu 100 000 £, přičemž cena akcie koná náhodnou
procházku s tím, že v průběhu roku buď může stoupnout o 10 % nebo klesnout o 12 %. Cílem
investiční strategie je na jedné straně neomezovat růstový potenciál a na druhé straně zamezit
poklesu hodnoty portfolia pod výchozí úroveň 100 000 £. K sipozici je obligace
s bezrizikovým výnosem 5 %.
(A)
100000
-12%
+10%
S = 70250
B = 31827
102077
(B)
88000
-12%
77440
(100000)
S=0
B = 95238
95238
+10%
96800
(100000)
(C)
110000
-12%
96800
(100000)
+10%
S = 95455
B = 15238
110693
121000
(121000)
žádoucí skladba portfolia v uzlu (B):
cílem je dosáhnout hodnoty 100 000 £ bez ohledu na pozdější býčí či medvědí vývoj
akciového trhu, portfolio musí být složeno výlučně z obligací v hodnotě
42
100000
= 95238
1 + 0,05
S =0
B=
žádoucí skladba portfolia v uzlu (C):
proporce mezi akciemi a obligacemi je dána řešením soustavy
1,1S + 1,05 B = 121000
0,88S + 1,05 B = 100000
⇒
S = 95455
B = 15238
žádoucí skladba portfolia v uzlu (A):
proporce mezi akciemi a obligacemi je dána řešením soustavy
1,1S + 1,05 B = 110693
0,88S + 1,05 B = 95238
S = 70250
⇒
B = 31827
počáteční hodnota pojištěného portfolia je vyšší než hodnota nezajištěného portfolia
(analogie placení pojistného)
♦
poznámky: - velikost transakčních nákladů při přeskupování portfolia snižuje výnosnost
cenných papírů resp. zvyšuje velkost počáteční investice
- potenciálně nestabilizující vliv v období větších cenových výkyvů (nákup
akcií a prodej obligací při růstu akciového trhu resp. prodej akcií a
nákup obligací při poklesu akciového trhu)
- strategie pojišťování je levnější pomocí futuritních kontraktů
růst cen akcií vede k doporučení nakupovat indexové futurity, které
vydělávají na růstu akciového trhu (vedle vlastního zhodnocování
držených akcií)
pokles cen akcií vede k doporučení prodávat indexové futurity, které
vydělávají na poklesu akciového trhu, čímž kompenzují pokles
hodnoty držených akcií
b) aktivní řízení obligačního portfolia
i) „znesoulaďování“ aktiv a pasív (mismatching)
zaujímání spekulační pozice záměrným vytvářením rozdílné doby splatnosti
pohledávek a závazků
očekávaný růst úrokových sazeb ⇒ zkracování aktiv a prodlužování pasiv ve
snaze oddalovat růst nákladů a urychlovat růst výnosů
očekávaný pokles úrokových sazeb ⇒ prodlužování aktiv a zkracování pasiv ve
43
snaze oddalovat pokles výnosů a urychlovat pokles nákladů
♦
Finanční manažer má možnost financovat nákup 3M CD s výnosem 10,25 % pomocí 3M
půjčky se sazbou 10,125 %. Současně se domnívá, že ode dneška za 1 měsíc úrokové sazby
poklesnou o 1 p.b.. Na výběr má tři investiční alternativy:
a) využit arbitrážovou příležitost
91
) = 1 025 555
příjem z CD = 1 000 000 × (1 + 0,1025 × 365
91
) = 1 025 543
splátka půjčky = 1 000 000 × (1 + 0,10125 × 365
zisk = 312
b) zakoupit 3M CD pomocí 1M půjčky a následně refinancovat dlužnickou pozici 2M
půjčkou
příjem z CD = 1 025 555
30
61
splátka půjčky = 1 000 000 × (1 + 0,10125 × 365
) × (1 + 09125 × 365
) = 1 023 699
zisk = 1856
c) zakoupit 3M CD pomocí 1M půjčky, CD po uplynutí měsíce prodat a výtěžek
investovat do 2M depozita
příjem z prodeje CD =
1 025 555
= 1 009 942
61
1 + 0,0925 × 365
30
) = 1 008 322
splátka půjčky = 1 000 000 × (1 + 0,10125 × 365
61
) = 1620 × 1,01525 = 1645
zisk = (1 009 942 − 1 008 322) × (1 + 0,09125 × 365
srovnání alternativ b) a c):
b): vyšší zisk 1856 po uplynutí 3 měsíců
c): nižší zisk po uplynutí 1 měsíce
♦
ii) switchování (swapování) obligací
techniky zaměňování (prodejů a nákupů) jedněch obligací jinými obligacemi s cílem
posílit výnos obligačního portfolia
- sebrání výnosu (pure yield pickup switch)
přechod k obligacím nabízejícím aktuálně vyšší kupón, vyšší výnos do splatnosti
popř. obojí
44
neprovádí se analýza očekávání úrokových sazeb, kreditních či výnosových spreadů
- úrokový anticipační switch (interest rate anticipation switch)
přeskupování obligačního portfolia s cílem vydělat na očekávaném pohybu
úrokových sazeb prostřednictví odlišné cenové citlivosti obligací s rozdílnou
délkou durace
∆P = − P ×
∆r
×D
1+ r
očekávaný pokles sazeb ⇒ prodlužování durace portfolia (vyšší růst ceny
zaznamenají obligace s delší durací)
očekávaný růst sazeb ⇒ zkracování durace portfolia (nižší cenový pokles
zaznamenají obligace s kratší durací)
- substituční switch (substitution switch)
motivace obchodu vychází z identifikace domnělých tržních anomálií v očekávání,
že během tzv. nápravného období (workout period) bude tržní anomálie
odstraněna
strategickým záměrem je nákup podhodnocených a prodej nadhodnocených aktiv
♦
Portfolio manažer identifikoval cenovou distorzi mezi následujícími dvěma obligacemi téže
rizikové třídy:
obligace A: kupón 10 % (vyplácen pololetně), splatnost 18 let, YTM 10 %
obligace B: kupón 10,25 % (vyplácen pololetně), splatnost 18,5 let, YTM 10,2 %
Manažer očekává, že během šesti měsíců do doby výplaty příštího kupónu se výnosy obou
obligací srovnají (dojde k odstranění cenové anomálie). Jak velký zisk lze očekávat od
techniky substitučního switche?
Zahájení switche
Výnos (%)
Ukončení switche
Cena
Výnos (%)
Cena
Obligace A
10
100
10
100
Obligace B
10,2
100,41
10
102,07
ceny obligací odpovídají současné hodnotě budoucího hotovostního toku obligace
zahájení switche: - krátký prodej jednoho kusu obligace A ⇒ příjem 100
45
- nákup 100:100,41 = 0,996 kusů obligace B ⇒ výdaj 100
ukončení switche: - nákup jednoho kusu obligace A ⇒ výdaj 100 + 5
- prodej obligací B ⇒ příjem
100
× (102,07 + 5,125) = 106,77
100,41
Substituční switch vydělává 1,77 peněžních jednotek na 100 peněžních jednotek
nominále.
♦
používá-li substituční switch obligace s výrazně odlišnou dobou do splatnosti (tedy
s odlišnou citlivostí ceny obligace na pohyb úrokové sazby), je nutné jej zajistit
(imunizovat) proti posunům výnosové křivky
imunizační pravidlo:
investice do A × durace A = investice do B × durace B
♦
Jaký by byl výsledek neimunizovaného substitučního switche z předchozího příkladu za
předpokladu, že obligaci B zbývá do splatnost 5,5 let a během nápravného období úrokové
sazby poklesnou o 1 p.b.?
Zahájení switche
Výnos (%)
Ukončení switche
Cena
Výnos (%)
Cena
Obligace A
10
100
9
108,73
Obligace B
10,2
100,21
9
104,95
Neimunizovaný substituční switch je ztrátový, neboť růst ceny obligace B v důsledku
odstranění cenové anomálie je více než převážen růstem ceny obligace A v důsledku její vyšší
citlivost na pokles úrokových sazeb.
♦
- kreditní spreadový switch
identifikace cenových anomálií (tj. fundamentálně podhodnocených a
nadhodnocených obligací) na bázi analýzy kreditního rizika
podhodnocené kreditní riziko ⇒ signál k prodeji obligace, jelikož lze očekávat
pokles ceny obligace v důsledku zvýšení kreditního spreadu
nadhodnocené kreditní riziko ⇒ signál k nákupu obligace, jelikož lze
46
očekávat růst ceny obligace v důsledku snížení kreditního spreadu
4. Měření výkonnosti portfolia
sledované aspekty: - ukazatele vhodné pro měření zhodnocení investovaných aktiv
- očištění výnosů o podstoupené riziko
- celkové vyhodnocení dosažených výnosů
a) měření výnosů portfolia
t1
V0
t2
tT
t3
CFT-1
CF2 CF2
CF1
CFT
hodnotou vážená (hodnotová) výnosová míra (money-weighted rate of return):
VT = V0 (1 + R ) t1 +...+ tT + CF1 (1 + R ) t 2 +...+ tT + ... + CFT −1 (1 + R ) tT
♦
Portfolio A
Počáteční
hodnota
Hotovostní
tok
Investovaná
částka
Zhodnocení
Koncová
hodnota
Portfolio B
1
2
3
4
1
2
3
4
100
240
126
138,6
100
120
198
107,8
100
-100
0
0
100
-100
200
140
126
100
220
98
20
-10
10
20
-10
10
240
126
138,6
120
198
107,8
hodnotová výnosová míra portfolia A:
100(1 + R A ) 4 + 100(1 + R A ) 4 − 100(1 + R A ) 3 = 138,6
R A = 6,83 %
hodnotová výnosová míra portfolia B:
100(1 + RB ) 4 + 100(1 + RB ) 3 − 100(1 + RB ) 2 = 107,8
RB = 1,52 %
♦
47
nevýhoda hodnotové míry: naměřená výkonnost portfolia je závislá na struktuře
hotovostního toku, kterou manažer portfolia obvykle nemůže ovlivnit
časem vážená (časová) výnosová míra (time-weighted rate of return)
⎛ V1
⎜⎜
⎝ V0
⎞
⎟⎟
⎠
t1 365
⎛ V2
⎞
⎟⎟
× ⎜⎜
⎝ V1 + CF1 ⎠
t 2 365
⎛
⎞
VT
⎟⎟
× .... × ⎜⎜
⎝ VT −1 + CFT −1 ⎠
tT −1 365
= (1 + R )
( t1 +...+ tT −1 ) 365
♦
Jaká je výkonnost portfolií A a B z předchozího příkladu měřená pomocí časové výnosové
míry?
⎛ 240 126 138,6 ⎞
×
×
RA = ⎜
⎟
⎝ 200 140 126 ⎠
⎛ 120 198 107,8 ⎞
RB = ⎜
×
×
⎟
98 ⎠
⎝ 100 220
13
− 1 = 5,91 %
13
− 1 = 5,91 %
♦
nevýhoda časové výnosové míry: znalost tržního ocenění aktiv portfolia v každém
okamžiku pohybu hotovostního toku
b) očistění výnosu o podstoupené riziko
klasifikace podle míry rizika:
- míry na bázi směrodatné odchylky
jsou vhodnější pro málo diverzifikovaná portfolia (dáno např. statutem
fondu)
- míry na bázi koeficientu beta
vhodné pro vysoce diverzifikovaná portfolia
klasifikace podle konstrukce ukazatele:
- míra dodatkového rizika
vhodná pro vyhodnocení rizikovosti investovaných prostředků
- míra diferenciálního rizika
vhodná pro komparaci s referenčním tržním portfoliem
i) Sharpeho míra dodatkového výnosu k volatilitě (excess return to volatility)
eS =
µP − µF
σP
48
Obrázek: Porovnání výkonnosti portfolií dle Sharpeho
µP
D●
M
●
C●
●
B
●
A
µF
σP
pořadí portfolií : A ≈ B p M p C ≈ D
ii) Treynorova míra dodatkového výnosu k beta (excess return to beta)
eT =
µP − µF
βP
Obrázek: Porovnání výkonnosti portfolií dle Treynora
µP
D●
M
●
C●
µF
●
A
●
B
βP
pořadí portfolií : A ≈ B p M p C ≈ D
iii) Jensenův index diferenciální výkonnosti (Jensen differential performance index)
e J = µ P − [µ F + ( µ M − µ F ) β P ]
porovnáván je výnos portfolia s výnosem stejně rizikového portfolia
ležícího na přímce SML (srovnání s „naivní“ investiční strategií držet
stejně rizikovou kombinaci bezrizikového a tržního portfolia)
49
Obrázek: Porovnání výkonnosti portfolií dle Jensena
µP
B
●
A
●
µF
●
ASML
●
M
SML
●
BSML
βP
pořadí portfolií : M p A p B