MBT1 – 4. týden
Transkript
MBT1 – 4. týden 1 L’Hospitalovo pravidlo 1. Spočtěte limity: a) lim x→0 2 tg x − x , x − sin x b) limπ x→ 2 tg(3x) , tg x c) lim x→0 ln(cos(ax)) , ln(cos(bx)) d) lim xx . x→0 Derivace funkce 2. Nalezněte derivace funkce f všude, kde tato derivace existuje: q p √ 2x a) f (x) = 1−x2 , b) f (x) = x + x + x, c) f (x) = ln(tg x2 ), √ , d) f (x) = arccos 1−x 2 e) f (x) = √ x x, x > 0, f) f (x) = (sin x)cos x + (cos x)sin x . √ 3. Napište rovnici tečny ke křivce y = (x + 1) 3 3 − x procházejı́cı́ bodem a) [−1, 0], b) [2, 3], c) [3, 0]. 4. Pod jakým úhlem se protı́najı́ křivky y = x2 a x = y 2 ? 5. Rozhodněte, zda existujı́ lokálnı́ nebo globálnı́ extrémy funkce na dané množině. Pokud ano, určete body těchto extrémů. a) x2 sin x, x ∈ [− π2 , π/ 2], b) x2 e−2x , x ∈ (0, +∞), x ∈ (−3, 3). 1 c) |x2 + x − 2| − |x2 − 3x + 2|, Výsledky: 1. 2, 1/3, (a/b)2 , 1; 2. a) 2(1 + x2 )/(1 − x2 )2 , |x| = 6 1, √ √ √ √ 1+2 x+4 x x+ x b) √ √ √ q √ √ , x > 0, 8 x x+ x x+ x+ x c) 1/(sin x), x ∈ (2kπ, (2k + 1)π), k ∈ Z, √ √ d) 1/ 1 + 2x − x2 , |x − 1| < 2, e) x1/x−2 (1 − ln x), x > 0, f) [(sin x)1+cos x ][cotg2 x − ln sin x] − [(cos x)1+sin x ][tg2 x − ln cos x], x ∈ (2kπ, 2kπ + π/2), k ∈ Z. 3. a) y = √ 3 4(x + 1), b) y = 3, c) y = 3. 4. 1. průsečı́k [0, 0] – úhel π/2, 2. průsečı́k [1, 1] – úhel π/2 − 2 arctg 12 . 5. a) maximum v bodě π/2, minimum v bodě −π/2, lokálnı́ extrémy nejsou, b) lokálnı́ i globálnı́ maximum v bodě 1, minimum neexistuje lokálnı́ ani globálnı́, c) lokálnı́ minimum v bodě 1, lokálnı́ maximum v bodě 1/2, globálnı́ extrémy nejsou. 2
Podobné dokumenty
Ukázka zápočtového testu č. 2 (jde o 2 varianty) 1) Nalezněte
 je limita −∞, zleva +∞, vodorovná asymptota y = 1, v +∞ se funkce blíží k asymptotě
shora, v −∞ zdola.
1b) Svislá asymptota x = 2, zprava i zleva je limita +∞; vodorovná asymptota y = 3, v +∞
se fu...
je limita −∞, zleva +∞, vodorovná asymptota y = 1, v +∞ se funkce blíží k asymptotě
shora, v −∞ zdola.
1b) Svislá asymptota x = 2, zprava i zleva je limita +∞; vodorovná asymptota y = 3, v +∞
se fu...
A + B
 9. Exponenciála a logaritmus. Předpokládejme, že a ∈ (0, 1) ∪ (1, ∞). Potom
ay = x
10y = x
ey = x
9. Exponenciála a logaritmus. Předpokládejme, že a ∈ (0, 1) ∪ (1, ∞). Potom
ay = x
10y = x
ey = x
str. 41, př. 1 Nakreslete grafy funkcí y=sinx, y=sin(x/2)
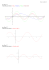 str. 41, př. 1
Nakreslete grafy funkcí y=sinx, y=sin(x/2), y=2sinx, y=sin(x+pi/6)
str. 41, př. 1
Nakreslete grafy funkcí y=sinx, y=sin(x/2), y=2sinx, y=sin(x+pi/6)
KMA-MMAN1
 a) y = x5 − 10x2 + x + 3, b) y = 2
, c) y = tg x,
x −1
d) y = cos x, e) y = sh x, f ) y = arctg x, g) y = x3 − 27x2 .
5. Určete asymptoty funkce:
a) y = x5 − 10x2 + x + 3, b) y = 2
, c) y = tg x,
x −1
d) y = cos x, e) y = sh x, f ) y = arctg x, g) y = x3 − 27x2 .
5. Určete asymptoty funkce:
1. Urcete definicn´ı obory následuj´ıc´ıch funkc´ı:
 Z prvnı́ podmı́nky plyne log2 (x + 4) 6= 3 ⇒ log2 (x + 4) 6= log2 8. Odlogaritmovánı́m obou
stran nerovnosti dostáváme x + 4 6= 8 ⇒ x 6= 4.
Z druhé podmı́nky plyne x > −4.
Celkově tedy Df = (−...
Z prvnı́ podmı́nky plyne log2 (x + 4) 6= 3 ⇒ log2 (x + 4) 6= log2 8. Odlogaritmovánı́m obou
stran nerovnosti dostáváme x + 4 6= 8 ⇒ x 6= 4.
Z druhé podmı́nky plyne x > −4.
Celkově tedy Df = (−...
POMNˇENKA
 Značení v Pomněnce . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Značení v Pomněnce . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Zadání 2A BC
 20. Máme 3 kontejnery s mraženými kuřaty. Ve druhém z nich je 45 % z celkového počtu kuřat. Průměrné hmotnosti
kuřat v jednotlivých kontejnerech jsou po řadě 1,2 kg, 1 kg a 1,5 kg. P...
20. Máme 3 kontejnery s mraženými kuřaty. Ve druhém z nich je 45 % z celkového počtu kuřat. Průměrné hmotnosti
kuřat v jednotlivých kontejnerech jsou po řadě 1,2 kg, 1 kg a 1,5 kg. P...
Test č.9
 Jestliže jedním kořenem rovnice x2 − m2 x − m + 1 = 0 (s neznámou x) je číslo x1 = 1, pak pro její
druhý kořen x2 platí
a) • x2 = 0 ∨ x2 = 3,
d) x2 = 0,
Jestliže jedním kořenem rovnice x2 − m2 x − m + 1 = 0 (s neznámou x) je číslo x1 = 1, pak pro její
druhý kořen x2 platí
a) • x2 = 0 ∨ x2 = 3,
d) x2 = 0,
 je dráha bodu A při šroubovém pohybu, kde ω je úhel otočenı́ a p posunutı́ bodu A.
Definice 5. Výška závitu v je velikost posunutı́ bodu při otočenı́ o 2π radiánů. Jestliže
otočı́me ...
je dráha bodu A při šroubovém pohybu, kde ω je úhel otočenı́ a p posunutı́ bodu A.
Definice 5. Výška závitu v je velikost posunutı́ bodu při otočenı́ o 2π radiánů. Jestliže
otočı́me ...
 4. Užitím definice monotonnosti na množině dokažte, že
k
a) funkce y =
je na intervalech (−∞; 0), (0, +∞) pro k > 0 klesající a pro k < 0
x
rostoucí.
5. Rozhodněte o paritě funkce
x3 sin x
x cos x
a...
4. Užitím definice monotonnosti na množině dokažte, že
k
a) funkce y =
je na intervalech (−∞; 0), (0, +∞) pro k > 0 klesající a pro k < 0
x
rostoucí.
5. Rozhodněte o paritě funkce
x3 sin x
x cos x
a...