doprovodný text
Transkript
Metoda nejmenšı́ch čtverců v Octave, Scilabu a v Matlabu Stanislav Daniš 10. dubna 2007 Metoda nejmenšı́ch čtverců (least square method) je založena na minimalizaci sumy druhých mocnin odchylek zadaných a upřesněných hodnot, S 2 (~ p) = N X (yi − f (xi , p~))2 wi , (1) i=1 kde p~ je vektor hledaných parametrů funkce f (x i , p~), xi a yi jsou vektory souřadnic bodů, kterými je prokládána závislost daná předpisem f (x i , p~). Bodů [xi , yi ] je celkem N, počet parametrů budeme označovat pı́smenem M). wi zde značı́ váhy jednotlivých bodů [x i , yi ]. Minimum hodnoty sumy čtverců S 2 (~ p) je dáno nulovou hodnotou gradientu S 2 (~ p) dle p~ (analogie s prvnı́ derivacı́ funkce jedné proměnné v minimu). Tuto podmı́nku můžeme zapsat soustavou rovnic N X ∂S 2 ∂f (xi , p~) = −2 (yi − f (xi , p~)) wi = 0. ∂pj ∂pj i=1 (2) Tuto soustavu rovnic můžeme snadno řešit např. v přı́padě lineárnı́ nebo kvadratické regrese, kdy (2) vedou na známé vztahy (pro lineárnı́ regresi f (x) = p 1 x + p0 ) N X yi = p 0 N + p 1 i=1 N X N X (3) xi i=1 yi xi = p 0 i=1 N X xi + p 1 i=1 N X x2i (4) i=1 a pro kvadratickou regresi (f (x) = p 2 x2 + p1 x + p0 ) N X yi = p 0 N + p 1 i=1 N X yi xi = p 0 i=1 N X i=1 yi x2i = p0 N X xi + p 2 i=1 N X i=1 N X xi + p 1 x2i + p1 N X (5) i=1 N X i=1 N X x2i + p2 x3i + p2 N X i=1 N X x3i (6) x4i . (7) i=1 i=1 i=1 x2i Obecně se však jedná o soustavu rovnic, kterou lze řešit pouze iteračně. To znamená, že z nějakého výchozı́ho odhadnutého řešenı́ se snažı́me najı́t skutečné řešenı́ minimalizujı́cı́ (1). Postup je následujı́cı́: nahradı́me v předpisu minima (2) hodnotu funkce f (x i , p~) a jejı́ derivace pomocı́ Taylorova rozvoje v okolı́ odhadu řešenı́ p~0 (omezı́me se na prvnı́ členy rozvoje): f (xi , p~) = f (xi , p~0 ) + M X ∂f (xi , p~0 ) m=1 1 ∂pm ∆pm ∂f (xi , p~) ∂pk M X ∂ 2 f (xi , p~0 ) ∂f (xi , p~0 ) + ∆pm . ∂pk ∂pk ∂pm m=1 = (8) Nynı́ dosadı́me rovnice (8) do (2) a zanedbáme kvadratické členy v ∆p m . To můžeme provést nebot’ jsou to členy druhého řádu a pokud nejsme s prvnı́ aproximacı́ řešenı́ p~0 přı́liš daleko od minima je jejich velikost malá. Po dosazenı́ a nezbytných algebraických úpravách dostaneme: M X m=1 " N X ∂f (xi , p~0 ) ∂f (xi , p~0 ) i=1 ∂pk ∂pm ∂ 2 f (xi , p~0 ) wi + (yi − f (xi , p~0 )) wi ∂pk ∂pm = N X (yi − f (xi , p~0 )) i=1 #! ∆pm = ∂f (xi , p~0 ) wi ∂pk (9) Pokud nejsme přı́liš daleko od skutečného minima sumy čtverců (1), můžeme zanedbat člen s druhou derivacı́ funkce f (xi , p~0 ). Tento člen se při numerickém hledánı́ minima (1) běžně zanedbává nejen z tohoto důvodu – výpočet druhé derivace u složitějšı́ch úloh nenı́ bez komplikacı́. Takže nakonec máme soustavu M rovnic pro složky vektoru změn parametrů ∆~ p vektoru řešenı́ p~0 . Složky vektoru ∆~ p nám udávajı́, jak máme změnit původnı́ parametry p~, abychom se vı́ce přiblı́žili minimu (1). M X m=1 N X ∂f (xi , p~0 ) ∂f (xi , p~0 ) i=1 ∂pk ∂pm wi ! ∆pm = N X (yi − f (xi , p~0 )) i=1 ∂f (xi , p~0 ) wi ∂pk (10) Nový vektor řešenı́ je dán jednoduchým vztahem p ~ = p~0 + ∆~ p. (11) Gaussova metoda Soustava rovnic (10) je známa jako Gaussova metoda minimalizace sumy čtverců (1). Pokud se podı́váme na rovnice (10) pozorněji, můžeme je snadno přepsat do maticového tvaru: ˆp = Jˆ ∗ ŵ ∗ yres Jˆ ∗ (Jˆ ∗ ŵ)0 ∆~ ˆ , (12) kde Jˆ je matice Jacobiánu (tj. derivacı́) definovaná předpisem Jˆ = ∂f (x1 ,~ p) ∂p1 ∂f (x1 ,~ p) ∂p2 ∂f (x2 ,~ p) ∂p1 ∂f (x2 ,~ p) ∂p2 ... ∂f (x1 ,~ p) ∂pM ∂f (x2 ,~ p) ∂pM ... .. . ... .. . ∂f (xN ,~ p) ∂p1 ∂f (xN ,~ p) ∂p2 .. . ∂f (xN ,~ p) ∂pM , (13) ŵ je diagonálnı́ matice váhových koeficientů jednotlivých bodů [x i , yi ], ŵ = w1 0 . . . 0 0 w1 . . . 0 .. .. .. . . . 0 0 . . . wN yres ˆ je vektor odchylek zadaných a vypřesněných hodnot y, yres ˆ = y1 − f (x1 , p~) y2 − f (x2 , p~) .. . yN − f (xN , p~) 2 , (14) (15) ˆp je vektor hledaných změn parametrů p a ∆~ ~. Apostrof ’ značı́ transpozici matice. Soustavě (10) se často řı́ká soustava normálnı́ch rovnic. Do soustavy (10) nynı́ dosadı́me nový vektor řešenı́ (11) a opakujeme postup, dokud rozdı́l sum čtverců nového a předchozı́ho řešenı́ nedosáhne zadané hodnoty. Směrodatné odchylky nalezených parametrů určı́me pomocı́ matice na levé straně (12), σ̂ = q (Jˆ ∗ (Jˆ ∗ ŵ))−1 s, (16) kde s je směrodatná odchylka hodnot y res, s= s S 2 (~ p) , ν (17) kde S 2 (~ p) je suma čtverců definovaná vztahem (1) a ν = N − M je počet stupňů volnosti. Matici Ĉ = (Jˆ ∗ (Jˆ ∗ ŵ))−1 , (18) se řı́ká kovariančnı́. Ukažme si použitı́ výše odvozených vztahů na jednoduchém přı́kladě lineárnı́ regrese. Mějme 5 dvojic bodů [xi , yi ], které chceme proložit (“fitovat“) lineárnı́ funkcı́ f (x) = ax+b s počátečnı́m odhadem řešenı́ a=2 a b=1. Body majı́ následujı́cı́ hodnoty, váhové faktory pokládáme rovné 1: 1 3.131 2 5.001 3 7.149 4 9.171 5 11.028 Výpočet zastavı́me, až bude rozdı́l sum čtverců dvou po sobě následujı́cı́ch iteracı́ menšı́ než 10−6 . Spočtěme sumu čtverců pro odhad řešenı́ [2,1]: 2 S (~ p) = N X (yi − f (xi , p~))2 wi = 0.069388. (19) i=1 Matice Jacobiánu Jˆ má jednoduchý tvar (~ p = [a, b]) Jˆ = ∂f (x1 ,~ p) p1 ∂f (x1 ,~ p) p0 ∂f (x2 ,~ p) p1 ∂f (x2 ,~ p) p0 ∂f (x3 ,~ p) p1 ∂f (x3 ,~ p) p0 ∂f (x5 ,~ p) p1 ∂f (x5 ,~ p) p0 0.1310000 0.0010000 0.1490000 0.1710000 0.0280000 ∂f (x4 ,~ p) p1 ∂f (x4 ,~ p) p0 Vektor yres ˆ má pro odhad řešenı́ tyto prvky: yres ˆ = = x1 x2 x3 x4 x5 1 1 1 1 1 ! (20) (21) Levá strana (12) je matice 2 × 2 (máme dvě rovnice pro dvě změny ∆~ p vektoru řešenı́), ˆp = Jˆ ∗ (Jˆ ∗ ŵ)∆~ 3 55 15 15 5 ! ˆp ∆~ (22) Podobně, pro pravou stranu (12) po dosazenı́ dostaneme 1.40400 0.48000 Jˆ ∗ ŵ ∗ yres ˆ = ! (23) . ˆp jsou dány řešenı́m soustavy rovnic Hledané změny parametrů ∆~ 55 15 15 5 ! ˆp = ∆~ 1.40400 0.48000 ! −0.0036000 0.1068000 ˆp = → ∆~ ! (24) Nový vektor řešenı́ má tedy tvar (původnı́ měl hodnoty [2 1]) 1.9964 1.1068 p~ = p~ + ∆~ p= ! (25) Suma čtverců pro nové řešenı́ je S 2 = 0.023178, rozdı́l sum čtverců nového a starého řešenı́, ∆S 2 = 0.046210, což je vı́ce než zadaná přesnost. Výše uvedeným způsobem spočteme nový ˆp. Pro kontrolu uvádı́m hodnoty vektorů a matic (mimo Jacobiánu J, ˆ který v vektor změn ∆~ našem přı́padě zůstává stejný nebot’ nezávisı́ na parametrech p ~). 55 15 15 5 ! yres ˆ = 0.027800 −0.098600 0.053000 0.078600 −0.060800 7.1054 · 10−15 1.7764 · 10−15 ˆp = ∆~ ! , (26) ˆp = → ∆~ 1.7764 · 10−16 −1.7764 · 10−16 ! (27) Vidı́me, že změny parametrů v této iteraci jsou velice malé, či–li nejspı́še jsem dosáhli minima (1). Suma čtverců pro nové řešenı́ je S 2 = 0.023178, rozdı́l sum čtverců nového a starého řešenı́, ∆S 2 = 2.1511 · 10−16 , což je méně než zadaná přesnost a řešenı́ bylo nalezeno. Zbývá spočı́tat směrodatné odchylky nalezených parametrů. Použijeme vztah (18), σ̂ = q (Jˆ ∗ (Jˆ ∗ ŵ))−1 s = 0.027796 0.092189 ! (28) , tj. hledané parametry funkce a a b jsou následujı́cı́ (počet platných mı́st je nadhodnocen): a = 1.996400 ± 0.027796 (29) b = 1.106800 ± 0.092189, (30) graficky je lineárnı́ regrese zachycena na obr.1 Podobně můžeme řešit, ”fitovat”, složitějšı́ funkce, např. f (x) = ae −bx . V tomto přı́padě je Jacobián o něco složitějšı́, postup však zůstává stejný. Jˆ = ∂f (x1 ,~ p) ∂p1 ∂f (x1 ,~ p) ∂p2 ∂f (x2 ,~ p) ∂p1 ∂f (x2 ,~ p) ∂p2 ... ... ∂f (xN ,~ p) ∂p1 ∂f (xN ,~ p) ∂p2 e−bx1 −axe−bx1 = e−bx2 −axe−bx2 ... e−bxN . . . −axe−bxN ! . (31) Pro data na obrázku č.2 dostáváme po sedmi iteracı́ch z počátečnı́ho odhadu řešenı́ p ~=[5 0] hodnoty upřesněných parametrů a = 0.983058 ± 0.016618 (32) b = 0.098947 ± 0.002250. (33) 4 12 data regrese 11 10 9 y 8 7 6 5 4 3 1 1.5 2 2.5 3 x 3.5 4 4.5 5 Obrázek 1: Lineárnı́ regrese V Octave (Scilabu/Matlabu) lze dı́ky snadným operacı́m s maticemi napsat skript, který bude hledat parametry prokládané funkce. Výpis takového programu gaussfit (otestován v Octave 2.1.57) je uveden nı́že. % % % % % % % % % % % % % % function [p,sigma,iter]=gaussfit(func,dfunc,x,y,p0,w,maxit,eps) funkce fituje body [x_i,y_i] funkci func Gaussovou metodou pouziti: [p,sigma,iter]=gaussfit(func,dfunc,x,y,p0,w,maxit,eps);, kde func = fitovana funkce dfunc = funkce pocitajici Jacobian x = x-ove souradnice fitovanych bodu y = y-ove souradnice fitovanych bodu p0 = odhad parametru w = vektor vah jednotlivych bodu (nepovinny parametr) maxit = maximalni pocet iteraci (nepovinny parametr) eps = max. odchylka sum rezidui nasledujich iteraci (nepovinne) funkce vraci dva sloupcove vektory - p je vektor parametru, sigma vektor smerodatnych odchylek a pocet probehlych iteraci N=length(x); M=length(p0); % pocet dat % pocet vypresnovanych parametru x=x(:); % timto udelam z x sloupcovy vektor y=y(:); % timto udelam z y sloupcovy vektor p0=p0(:); % timto udelam z p0 sloupcovy vektor if (nargin>6) % je zadan vektor vah w=eye(N)*w(:); % w je nyni ctvercova diagonalni matice else w=eye(N); % pokud nejsou zadany vahy bodu, je w jednotkova matice end; 5 0.9 data regrese 0.8 0.7 0.6 y 0.5 0.4 0.3 0.2 0.1 0 -0.1 0 10 20 30 40 50 x 60 70 80 90 100 Obrázek 2: Nelineárnı́ regrese if (nargin<7) maxit=100;end; % maximalni pocet iteraci if (nargin<8) eps=1e-6;end; % max. odchylka sum rezidui nasledujich iteraci % prealokuji pamet na matice a vektory potrebne pro vypocty J=zeros(M,N); % Jacobian (M radku, N sloupcu) yres=zeros(N,1); % vektor rezidui y-p*x % nyni spoctu sumu rezidui pro prvotni odhad p0 S0=sum((y-feval(func,x,p0)).^2); deltaS=1; % prednastavena hodnota rozdilu rezidui iter=0; % pocitadlo iteraci p=p0; % cyklus vypresnovani while (iter<maxit & deltaS>eps); % cyklus je ukoncen po dosazeni max.poctu iteraci nebo zadane presnosti % spoctu matici Jacobianu, ta je nezavisla na y J=feval(dfunc,x,p); % spoctu yres=y-func(x,p) yres=y-feval(func,x,p); % spoctu pomocne matice LeveStrany a PraveStrany PS=J*w*yres; LS=J*(J*w)’; % a nyni uz pocitam posunuti parametru smerem k minimu dp=LS\PS; % tj. inv(LS)*PS % nove parametry p=p+dp; 6 % suma rezidui pro nove parametry Sn=sum((y-feval(func,x,p)).^2); % odchylka sum rezidui deltaS=abs(S0-Sn); iter=iter+1; S0=Sn; end % pokud je dosazeno maximalniho poctu iteraci, zobrazi se % varovani if (iter>=maxit) disp(’Vypocet zastaven po dosazeni maximalniho poctu iteraci.’); disp(’Zrejme nebylo dosazeno minima.’); disp(’Zadejte jiny pocatecni odhad p0.’) end % cyklus ukoncen, pocitaji se smerodatne odchylky nu=N-M; % pocet stupnu volnosti s=sqrt(S0/nu); sigma=diag(sqrt(inv(LS))*s); sigma=sigma(:); % opet prevedu na sloupcovy vektor % no, a to je vse, zbyva jen vypsat nejak uhledne vysledky for k=1:M fprintf(’p(%d)=%f +/- %f\n’,k,p(k),sigma(k)); end 7 Levenberg–Marquardtova metoda Gaussova metoda má určitou nevýhodu – občas se stane, že matice na levé straně rovnice (12) je špatně podmı́něná nebo je dokonce singulárnı́. Tomu se snažı́ zamezit metoda Levenberg—Marquardtova, která zavádı́ tlumı́cı́ faktor (damping factor) λ, λ > 0. Soustava rovnic (10) pak má tvar (srovnejte s relaxačnı́mi metodami řešenı́ rovnic (Gauss–Seidel)) M X m=1 N X ∂f (xi , p~0 ) ∂f (xi , p~0 ) i=1 ∂pk ∂pm ! wi + λδkm ∆pm = N X (yi − f (xi , p~0 )) i=1 ∂f (xi , p~0 ) wi . ∂pk (34) V maticovém zápisu má (34) tvar n o ˆp = Jˆ ∗ ŵ ∗ yres Jˆ ∗ (Jˆ ∗ ŵ)0 + Iλ ∆~ ˆ , (35) kde I je jednotková matice. Levenbergova–Marquardtova metoda pracuje následovně: 1. zvolı́me nějakou kladnou hodnotu λ 0 , a čı́slo µ > 1 2. spočteme prvnı́ iteraci pro λ = λ 0 a poté pro λ = λ0 µ 3. jsou–li obě iterace horšı́ než prvnı́ odhad (podle zvoleného kritéria), je tlumı́cı́ faktor λ zvětšen na λµ a výpočet dalšı́ iterace je opakován tak dlouho, dokud nenı́ nalezena hodnota λµk pro nějaké k, která vede ke zlepšenı́ řešenı́. 4. poté je nalezená hodnota λ použita pro dalšı́ iteraci stejným postupem jako v bodě 2. Nı́že naleznete výpis programu lmfit (otestován v Octave 2.1.57), který zavedenı́m relaxačnı́ho parametru λ upravuje původnı́ Gaussovu metodu na Levenbergovu–Marquardtovu. function [p,sigma,iter]=lmfit(func,dfunc,x,y,p0,w,maxit,eps,lambda,mu) % funkce fituje body [x_i,y_i] funkci func % Levenberg-Marquardtovou metodou % pouziti: [p,sigma,iter]=lmfit(func,dfunc,x,y,p0,w,maxit,eps,lambda,mu); % kde func = fitovana funkce % dfunc = funkce pocitajici Jacobian % x = x-ove souradnice fitovanych bodu % y = y-ove souradnice fitovanych bodu % p0 = odhad parametru % w = vektor vah jednotlivych bodu (nepovinny parametr) % maxit = maximalni pocet iteraci (nepovinny parametr) % eps = max. odchylka sum rezidui nasledujich iteraci (nepovinne) % lambda = tlumici faktor (damping faktor) % mu = korekcni faktor pro tlumici faktor % % funkce vraci dva sloupcove vektory - p je vektor parametru, % sigma vektor smerodatnych odchylek a pocet probehlych iteraci N=length(x); M=length(p0); % pocet dat % pocet vypresnovanych parametru x=x(:); % timto udelam z x sloupcovy vektor 8 y=y(:); p0=p0(:); % timto udelam z y sloupcovy vektor % timto udelam z p0 sloupcovy vektor if (nargin==6) % je zadan vektor vah w=eye(N)*w(:); % w je nyni ctvercova diagonalni matice else w=eye(N); % pokud nejou zadany vahy bodu, je w jednotkova matice end; if if if if (nargin<7) maxit=100;end; % maximalni pocet iteraci (nargin<8) eps=1e-6;end; % max. odchylka sum rezidui nasledujich iteraci (nargin<9) lambda=5;end; % tlumici faktor (damping faktor) (nargin<10) mu=1.05;end; % korekce pro tlumici faktor % prealokuji pamet na matice a vektory potrebne pro vypocty J=zeros(M,N); % Jacobian (M radku, N sloupcu) yres=zeros(N,1); % vektor rezidui y-p*x % nyni spoctu sumu rezidui pro prvotni odhad p0 S0=sum((y-feval(func,x,p0)).^2); deltaS=1; % prednastavena hodnota rozdilu rezidui iter=0; % pocitadlo iteraci % prvni iterace p=p0; Sn=S0; % cyklus vypresnovani while (iter<maxit & deltaS>eps); % cyklus je ukoncen po dosazeni max.poctu iteraci nebo zadane presnosti % spoctu matici Jacobianu J=feval(dfunc,x,p); % spoctu yres=y-func(x,p) yres=y-feval(func,x,p); % spoctu pomocne matice LeveStrany a PraveStrany % pro lambda PS=J*w*yres; LS=J*(J*w)’+eye(M)*lambda; % a nyni uz pocitam posunuti parametru smerem k minimu dp1=LS\PS; % tj. inv(LS)*PS Sn1=sum((y-feval(func,x,p+dp1)).^2); % a pro lambda/mu PS=J*w*yres; LS=J*(J*w)’+eye(M)*lambda/mu; % a nyni uz pocitam posunuti parametru smerem k minimu dp2=LS\PS; % tj. inv(LS)*PS Sn2=sum((y-feval(func,x,p+dp1)).^2); 9 % a nyni testuji, zda-li jsme se priblizil minimu if (Sn<Sn1 & Sn<Sn2) % neuspel jsem, je treba hledat dal (lambda->lambda*mu^k) k=1; while (Sn1>Sn & k<maxit) % dokud jsem horsi nez predtim % pocitam jen levou stranu, prava zustava stejna LS=J*(J*w)’+eye(M)*lambda*mu^k; % a nyni uz pocitam posunuti parametru smerem k minimu dp=LS\PS; % tj. inv(LS)*PS Sn1=sum((y-feval(func,x,p+dp1)).^2); k=k+1; end % nove parametry p=p+dp1; lambda=lambda*mu^(k-1); % nova hodnota lambda elseif (min(Sn1,Sn2)<Sn) % alespon jedno priblizeni je lepsi if (Sn1<Sn2) % Sn1 je lepsi (tj. lambda) % nove parametry p=p+dp1; Sn=Sn1; else % Sn2 je lepsi (tj. lambda/mu) % nove parametry p=p+dp2; lambda=lambda/mu; % nova hodnota lambda Sn=Sn2; end end % odchylka sum rezidui deltaS=abs(S0-Sn); iter=iter+1; S0=Sn; end; % pokud je dosazeno maximalniho poctu iteraci, zobrazi se % varovani if (iter>=maxit) disp(’Vypocet zastaven po dosazeni maximalniho poctu iteraci.’); disp(’Zrejme nebylo dosazeno minima.’); disp(’Zadejte jiny pocatecni odhad p0.’) end % cyklus ukoncen, pocitaji se smerodatne odchylky nu=N-M; % pocet stupnu volnosti s=sqrt(S0/nu); sigma=diag(sqrt(inv(LS))*s); sigma=sigma(:); % opet prevedu na sloupcovy vektor % no, a to je vse, zbyva jen vypsat nejak uhledne vysledky for k=1:M fprintf(’p(%d)=%f +/- %f\n’,k,p(k),sigma(k)); end 10 Simplexová metoda Určitou nevýhodou předchozı́ch metod může být potřeba počı́tat i derivaci funkce dle hledaných parametrů (Jacobián). Tuto nevýhodu odstraňuje metoda simplexů. Protože však i zde chceme vědět směrodatné odchylky nalezených parametrů, budeme muset hodnoty prvků kovariančnı́ matice Cij určit numericky. Metoda simplexů zavádı́ (n+1) n–tice, vektory, odhadů parametrů a vytvářı́ z nich v prostoru parametrů těleso o (n+1)–vrcholech – simplex. V přı́padě lineárnı́ regrese (2 hledané parametry) je simplexem trojúhelnı́k. Pro vrcholy simplexu (tedy různé hodnoty hledaných parametrů p~) spočteme hodnoty sum čtverců (1) a určı́me nejlepšı́ (P b (best)) a nejhoršı́ (Pw (worst)) přiblı́ženı́ (podle velikosti hodnot S 2 ). Z tohoto prvnı́ho kroku se pak hledá minimum sumy čtverců tak, že měnı́me podle určitého algoritmu souřadnice nejhoršı́ho bodu P w . Na vrchol Pw simplexu se aplikujı́ následujı́cı́ operace: • reflexe – tato operace zrcadlı́ bod P w těžištěm simplexu P̄ tak, že původnı́ a nová vzdálenost zrcadleného bodu od těžiště je α|P w P̄ | = |P ∗ P̄ |, kde P ∗ je označuje zrcadlený bod a α je koeficient reflexe (α > 0). P ∗ = (1 + α)P̄ − αPw . (36) • expanze – pokud zrcadlenı́ Pw vedlo k nalezenı́ nové minimálnı́ hodnoty sumy čtverců pro nový bod P ∗ (tj. S 2 (Pb ) > S 2 (P ∗ )) , provedeme expanzi, P ∗∗ = (1 − γ)P̄ + γP ∗ , (37) kde γ > 1 je koeficient expanze. Pokud je nový bod P ∗∗ lepšı́ než původnı́ zrcadlený P ∗ , zaměnı́me Pw za P ∗∗ , pokud ne tak zaměnı́me Pw za P ∗ . • kontrakce – pokud zrcadlenı́ Pw na P ∗ nevede k novému minimu, rozhoduje algoritmus následovně: je–li nový bod P ∗ jen o málo lepšı́ než původnı́ P w (tj. druhý nejhoršı́, S 2 (P ∗ ) > S 2 (Pi ), i 6= w), zaměnı́me Pw za P ∗ a provedu kontrakci P ∗∗ = (1 − β)P̄ + βPw , (38) kde β ∈< 0, 1 > je koeficient kontrakce. Pokud je zrcadlený bod po reflexi P ∗ horšı́, než původnı́ Pw , provedeme kontrakci rovnou. Je–li suma čtverců pro bod P ∗∗ po kontrakci S 2 (P ∗∗ ) > min(Pw , P ∗ ), tj. kontrakce nevedla ke zlepšenı́, nahradı́me všechny body simplexu novými body dle předpisu Pi + P b . (39) Pi = 2 Jen připomı́nám, že Pi jsou n-tice, tj. n-rozměrné vektory. Jednoduchost simplexové metody je ”vykoupena” citlivostı́ k nastavenı́ počátečnı́ho odhadu p~0 a k volbě parametrů α, β a γ. Tı́m, že nemáme k dispozici gradient sumy čtverců dle parametrů p~ (Jakobián), nevı́me přesně, kde se nacházı́ minimum a kam se máme se simplexem posunout. Pro nalezenı́ minima tak potřebujeme vı́ce iteracı́, častěji se také stává, že simplex uvı́zne v blı́zkém lokálnı́m minimu. Na obrázku č.3 vidı́te srovnánı́ ”fitovánı́” exponenciálnı́ funkce f (x) = ae −bx . Simplexovou metodou bylo po asi 100 iteracı́ch a změnách parametrů α, β a γ dosaženo minima pro hodnoty aab a = 1.07038 ± 0.0201756 (40) b = 0.11038 ± 0.0027817. (41) 11 1 data regrese simplex 0.8 y 0.6 0.4 0.2 0 -0.2 0 10 20 30 40 50 x 60 70 80 90 100 Obrázek 3: Srovnánı́ vypřesněnı́ simplexovou metodou a Gaussovou metodou. % % % % % % % % % % % % % % function [par,sigma,iter]=simplex(func,x,y,p0,maxit,eps,coef) funkce fituje body [x_i,y_i] funkci func Simplexovou metodou pouziti: [par,sigma,iter]=simplex(func,x,y,p0,maxit,eps,coef);, kde func = fitovana funkce x = x-ove souradnice fitovanych bodu y = y-ove souradnice fitovanych bodu p0 = odhad parametru maxit = maximalni pocet iteraci (nepovinny parametr) eps = max. odchylka sum rezidui nasledujich iteraci (nepovinne) coef = vektor koeficientu alfa, beta a gamma (reflexe, kontrakce a expanze) funkce vraci dva sloupcove vektory - p je vektor parametru, sigma vektor smerodatnych odchylek a pocet probehlych iteraci if (nargin<5) maxit=50;end; % maximalni pocet iteraci if (nargin<6) eps=1e-6;end; % max. odchylka sum rezidui nasledujich iteraci if (nargin<7) % vektor koeficientu alfa, beta a gamma alfa=2./3.; % koef. reflexe beta=0.5; % koef. kontrakce gamma=2; % koef. expanze else alfa=coef(1); beta=coef(2); gamma=coef(3); end M=length(p0); N=length(x); % pocet parametru % pocet dat 12 Obrázek 4: Základnı́ operace simplexové metody. x=x(:); y=y(:); p0=p0(:); % timto udelam z x sloupcovy vektor % timto udelam z y sloupcovy vektor % timto udelam z p0 sloupcovy vektor % prealokace pameti parametru (pomoci matice, co sloupec, to vrchol simplexu) p=zeros(M,M+1); dp=max(p0)/M; % krok zmeny parametru p_i (mozno nastavit jinak) for jj=1:M+1 p(:,jj)=p0+round((jj-(M+1)/2)-0.5)*dp; % j-ty sloupec je zaplnen p0 (preveden na sloupcovy vektor) % mozno napsat lepe end % p=p+eye(M,M+1)*dp % v kazdem sloupci zmenim jednu hodnotu parametru o dp % p=[0 0 2;0 2 0]; % a tady zacina iteracni cyklus iter=0; % pocitadlo iteraci deltaS=1; % rozdil sum ctvercu nejhorsiho a nejlepsiho reseni v danem kroku 13 while (iter<maxit & deltaS>eps) % spoctu sumy ctvercu pro (n+1)- rozmerny simplex S=zeros(M+1,1); for j=1:M+1 S(j)=sum((y-feval(func,x,p(:,j))).^2); end % nyni vyhledam nejlepsi a nejhorsi vrchol simplexu % funkce min a max mohou vratit i index min (max) prvku [Sb,b]=min(S); % nejlepsi (best) [Sw,w]=max(S); % nejhorsi (worst) % a jeste najdu druhy nejhorsi bod Shlp=S; Shlp(w)=S(b); % nejhorsi zamenim za nejlepsi [Sw2,w2]=max(Shlp); % a nyni mam 2 nejhorsi (2nd worst) % spoctu teziste simplexu T (vynecham nejhorsi bod) T=zeros(M,1); for j=1:M if (j~=w) T=p(:,j)+T;end; end; T=T/M; % spoctu souradnice reflektovaneho bodu P^*=R a sumu ctvercu R=(1.0+alfa)*T-alfa*p(:,w); SR=sum((y-feval(func,x,R)).^2); % je novy bod novym minimem? if (SR<Sb) % spoctu expanzi P^**=E a sumu ctvercu E=(1-gamma)*T+gamma*R; SE=sum((y-feval(func,x,E)).^2); if (SE<Sb) % E je novym minimem p(:,w)=E; % prohodim P_w za E S(w)=SE; else % E neni novym minimem, P_w nahradim R p(:,w)=R; % prohodim P_w za R S(w)=SR; end % reflektovany bod neni novym minimem elseif (SR>Sw2) % je R horsi nez druhy nejhorsi? if (SR<Sw) % je R lepsi nez worst? p(:,w)=R; % prohodim P_w za R S(w)=SR; end % provedu kontrakci K K=beta*p(:,w)+(1.0-beta)*T; SK=sum((y-feval(func,x,K)).^2); 14 if (SK>min(Sw,SR)) % je K horsi nez min(w,R)? % zamenim vsechny souradnice simplexu for j=1:M+1 pnove(:,j)=(p(:,j)+p(:,b))/2.0; end p=pnove; else p(:,w)=K; % prohodim P_w za K S(w)=SK; end else p(:,w)=R; % prohodim P_w za R S(w)=SR; end iter=iter+1; deltaS=abs(Sb-Sw)/Sb; % fprintf(’%d %f %f\n’,iter,p(1,b),p(2,b)); end % iterace skonceny % pokud je dosazeno maximalniho poctu iteraci, zobrazi se % varovani if (iter>=maxit) disp(’Vypocet zastaven po dosazeni maximalniho poctu iteraci.’); disp(’Zrejme nebylo dosazeno minima.’); disp(’Zadejte jiny pocatecni odhad p0.’) end % nyni spoctu prvky matice Jacobianu pomoci def.derivace dpar=1e-5; par=p(:,b); J=zeros(M,N); % J je matice (M x N) for j=1:M p2=par; p2(j)=p2(j)+dpar; for i=1:N J(j,i)=(feval(func,x(i),p2)-feval(func,x(i),par))/dpar; end end s=sqrt(Sb/(N-M)); % smerodatna odchylka C=inv(J*J’); % korelacni matice sigma=diag(sqrt(C)*s); % smerodatne odchylky hledanych parametru 15
Podobné dokumenty
IAJCE Přednáška č. 10 1 každému znaku je nutné přiřadit
 o Vrací podřetězec od pozice start
Instanční metoda string Substring(int startIndex, int N)
o Vrací podřetězec od pozice start délky N znaků
o Příklad:
string osloveni = "Mile deti!";
string koho =...
o Vrací podřetězec od pozice start
Instanční metoda string Substring(int startIndex, int N)
o Vrací podřetězec od pozice start délky N znaků
o Příklad:
string osloveni = "Mile deti!";
string koho =...
22 Riemannova metrika a obsah plochy
 Necht’ plocha Γ je určena rovnicemi x = s, y = t a z = es a křivka γ na této ploše je
definována rovnicemi x = cos τ a y = sin τ , kde τ ∈ h0, 2πi.
Pak délka této křivky na dané ploše je
Necht’ plocha Γ je určena rovnicemi x = s, y = t a z = es a křivka γ na této ploše je
definována rovnicemi x = cos τ a y = sin τ , kde τ ∈ h0, 2πi.
Pak délka této křivky na dané ploše je
Masarykova Univerzita Plošná fotometrie eliptických galaxi´ı
 Obě spirálnı́ skupiny jsou členěny na tři poddruhy podle poměru jasnosti galaktické výdutě
a disku a podle mı́ry zatočenı́ (rozevřenı́) spirálnı́ch ramen (k označenı́ se přidávajı́ m...
Obě spirálnı́ skupiny jsou členěny na tři poddruhy podle poměru jasnosti galaktické výdutě
a disku a podle mı́ry zatočenı́ (rozevřenı́) spirálnı́ch ramen (k označenı́ se přidávajı́ m...
Matematicka´ poha´dka
 vylézá derivace ze svého doupěte. Zahlédla bojovnı́ka a vrhá
se na něj. Arcus však neotálı́ a útočı́ svým integračnı́m mečem,
exponenciálnı́m štı́tem kryje každý pokus o zderivova...
vylézá derivace ze svého doupěte. Zahlédla bojovnı́ka a vrhá
se na něj. Arcus však neotálı́ a útočı́ svým integračnı́m mečem,
exponenciálnı́m štı́tem kryje každý pokus o zderivova...
Řešení V. série
 kládejme (pro spor) různé energie ve dvou různých bodech povrchu. Na křivce parametrizované
t, která body spojuje, je energie spojitou funkcí t a podle věty o střední hodnotě zde existuje
bod s nen...
kládejme (pro spor) různé energie ve dvou různých bodech povrchu. Na křivce parametrizované
t, která body spojuje, je energie spojitou funkcí t a podle věty o střední hodnotě zde existuje
bod s nen...
Počítačová Tomografie Werth
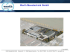 Počítačová tomografie integrovaná do multisenzorového souřadnicového měřicího stroje
- Měření velkých dílců a komponentů s vysokou hustotou VT-A-7-3-0328_E
Počítačová tomografie integrovaná do multisenzorového souřadnicového měřicího stroje
- Měření velkých dílců a komponentů s vysokou hustotou VT-A-7-3-0328_E
nemer volkswagen
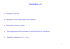 X · rot X = X · (X × y) = 0
Protože X ̸= 0 a rot X =
̸ 0 (nesplněni integrability) předchozı́ rovnice je
nutnou podmı́nkou pro existenci µ. (t.j., existence µ ⇒ X · rot X = 0 )
Na druhé straně...
X · rot X = X · (X × y) = 0
Protože X ̸= 0 a rot X =
̸ 0 (nesplněni integrability) předchozı́ rovnice je
nutnou podmı́nkou pro existenci µ. (t.j., existence µ ⇒ X · rot X = 0 )
Na druhé straně...
Spektrální a korelační analýza
 • používá se pro detekci rytmů, které jsou společné mezi
dvěma signály (v případě EEG v obou hemisférách)
• CCF má stejnou frekvenci jako složka, která je
přítomna v obou kanálech
• používá se pro detekci rytmů, které jsou společné mezi
dvěma signály (v případě EEG v obou hemisférách)
• CCF má stejnou frekvenci jako složka, která je
přítomna v obou kanálech