Vestav né funkce
Transkript
119
Vestav né funkce
Následující strany obsahují seznam funkcí podle oblastí a jejich krátký popis. Funkce
se značkou "pro" se vyskytují pouze u verze Mathcad Professional. Další informace
o funkcích a jejich argumentech najdete v nápovědě.
V tomto seznamu značí:
•
x, y - reálná čísla,
•
z - reálné nebo komplexní číslo,
•
m, n, i, j, k - celá čísla,
•
S a všechny názvy začínající S - řetězcové proměnné (viz. kap. 4.2.3),
•
v, u a každé jméno začínající v - vektory,
•
A, B - matice nebo vektory,
•
M, N - čtvercové matice,
•
F - vektor funkcí,
•
cesta - umístění souboru (řetězcová proměnná).
Význam dalších proměnných je vysvětlen přímo u konkrétních funkcí.
Jestliže je argument či výsledek nějaké funkce úhel a není uvedena jednotka, jedná se
o úhel v radiánech. U funkcí, jejichž výsledkem je více hodnot, dostáváme pouze
hodnotu základní.
U názvu funkcí rozlišujte malá a velká písmena (kromě funkce Find). Na použitém
fontu nezáleží.
Seznamy
120
Goniometrické funkce
sin(z)
sinus
cos(z)
kosinus
tan(z)
tangens
cot(z)
kotangens
sec(z)
sekans
csc(z)
kosekans
Inverzní goniometrické funkce
asin(z)
inverzní sinus
acos(z)
inverzní kosinus
atan(z)
inverzní tangens
Hyperbolické funkce
sinh(z)
hyperbolický sinus
cosh(z)
hyperbolický kosinus
tanh(z)
hyperbolický tangens
coth(z)
hyperbolický kotangens
sech(z)
hyperbolický sekans
csch(z)
hyperbolický kosekans
Inverzní hyperbolické funkce
asinh(z)
inverzní hyperbolický sinus
acosh(z)
inverzní hyperbolický kosinus
atanh(z)
inverzní hyperbolický tangens
Exponenciální a logaritmické funkce
exp(z)
ez
log(z)
logaritmus se základem 10 čísla z (dekadický
logaritmus)
Seznamy
121
logaritmus se základem e čísla z (přirozený
logaritmus)
ln(z)
Funkce pro ešení rovnic
root(f(z), z)
hodnota z, kdy je funkce f(z) nulová
polyroots(v)
vektor kořenů polynomu n-tého stupně, jehož
n+1 koeficientů je uvedeno ve vektoru v
pro
lsolve(M, vp)
řešení soustavy lineárních rovnic
Find(z1, z2, ...)
řešení soustavy rovnic pro neznámé z1, z2, ...
Minerr(z1, z2, ...)
přibližné řešení soustavy rovnic
Vektorové a maticové funkce
matrix(m, n, f)
matice, ve které prvek i, j odpovídá funkci f(i, j),
kde i = 0 .. m-1 a j = 0 .. n-1
augment(A, B)
pole, které vzniklo spojením polí A, B o stejném
počtu řádek (vedle sebe)
stack(A, B)
pole, které vzniklo spojením polí A, B o stejném
počtu sloupců (nad sebou)
submatrix(A, ir, jr, ic, jc)
submatice, která vznikla z řádků ir až jr a
sloupců ic až jc matice A
cols(A)
počet sloupců matice A
rows(A)
počet řádků matice A
length(v)
počet prvků vektoru v
last(v)
index posledního prvku vektoru v
max(A)
největší prvek matice A
min(A)
nejmenší prvek matice A
identity(n)
jednotková matice I o rozměru n x n
diag(v)
pro
diagonální matice obsahující na diagonále prvky
vektoru v
geninv(A)
pro
matice L, která je levou inverzí matice A
(L A = I)
rref(A)
matice, která má odstupňovaný kanonický tvar
(row-reduced echelon form)
Seznamy
122
tr(M)
součet prvků na diagonále čtvercové matice M
(stopa)
rank(A)
hodnost matice A reálných čísel
norm1(M)
pro
norma L1 matice M
norm2(M)
pro
norma L2 matice M
norme(M)
pro
Euklidovská norma matice M
normi(M)
pro
norma L∞ matice M
cond1(M)
pro
číslo podmíněnosti matice M založené na
normě L1
cond2(M)
pro
číslo podmíněnosti matice M založené na
normě L2
conde(M)
pro
číslo podmíněnosti matice M založené na
Euklidovské normě
condi(M)
pro
číslo podmíněnosti matice M založené na
normě L∞
eigenvals(M)
vektor vlastních hodnot matice M
eigenvec(M, z)
normovaný vlastní vektor odpovídající vlastní
hodnotě z čtvercové matice M
eigenvecs(M)
pro
matice obsahující ve sloupcích normované
vlastní vektory odpovídající vlastním hodnotám
matice M (n-tý sloupec odpovídá n-té vlastní
hodnotě)
genvals(M, N)
pro
vektor v vlastních hodnot, které vyhovují
zobecněné úloze M x = vi N x, když x obsahuje
odpovídající vlastní vektory
genvecs(M, N)
pro
matice obsahující normované vlastní vektory
odpovídající vlastním hodnotám získaným
pomocí funkce genvals
cholesky(M)
pro
dolní trojúhelníková matice L, pro kterou platí
L LT = M (předpokládá symetrickou matici M a
používá pouze její horní trojúhelníkovou část)
qr(A)
pro
matice, jejíž prvních n sloupců tvoří čtvercová,
ortonormální matice Q a ostatní sloupce obsahují
horní trojúhelníkovou matici R, platí A = Q R
lu(M)
pro
matice tvořená třemi čtvercovými maticemi P, L,
U, které mají stejný rozměr jako M a odpovídají
rovnici P M = LU, matice L resp. U jsou dolní
resp. horní trojúhelníkové matice
Seznamy
123
svds(A)
pro
vektor obsahující singulární hodnoty reálné
matice A
svd(A)
pro
matice obsahující dvě matice U (m x n), V (n x n)
nad sebou takové, že vyhovují rovnici
A = U diag(s) VT, kde s je vektor obsahující
prvních n prvků získaných pomocí funkce
svds(A)
Funkce pracující se soubory a obrázky
READ("cesta")
hodnoty přečtené z nestrukturovaného datového
souboru
(čísla
oddělená
mezerami
kombinovanými s tabelátory), výsledkem je
skalár (první číslo ze souboru) nebo vektor
prvních n hodnot (pokud funkci přiřadíme
indexované proměnné, která má n prvků)
READPRN("cesta")
pole hodnot přečtených ze strukturovaného
datového souboru (čísla uspořádaná v řádcích a
sloupcích
oddělených
mezerou
nebo
tabelátorem), výsledkem je vektor nebo matice
READBMP("cesta")
pole hodnot 0 až 255 reprezentující černobílou
bitovou mapu obrázku (.bmp)
READ_IMAGE("cesta")
pro
obdoba funkce READBMP, ale můžeme pracovat
i s obrázky formátu GIF, JPG a TGA.
pole hodnot reprezentující tři matice barev
(červených, zelených a modrých) odpovídajícího
obrázku vedle sebe (ve verzi Mathcad
Professional je možné pracovat nejen s obrázky
ve formátu BMP, ale i s formáty GIF, JPG a
TGA)
READRGB("cesta")
READ_RED("cesta")
pro
první třetina hodnot funkce READRGB
READ_GREEN("cesta")
pro
druhá třetina hodnot funkce READRGB
READ_BLUE("cesta")
pro
poslední třetina hodnot funkce READRGB
READ_HLS("cesta")
pro
pole hodnot reprezentující tři matice informací
o barvách
(odstín,
světelnost,
sytost)
odpovídajícího obrázku vedle sebe
READ_HLS_HUE("cesta")
pro
první třetina hodnot funkce READ_HLS
READ_HLS_LIGHT("cesta") pro
druhá třetina hodnot funkce READ_HLS
READ_HLS_SAT("cesta")
pro
poslední třetina hodnot funkce READ_HLS
Seznamy
124
READ_HSV("cesta")
pro
pole hodnot reprezentující tři matice informací
o barvách
(odstín,
sytost,
hodnota)
odpovídajícího obrázku vedle sebe
READ_HSV_HUE("cesta")
pro
první třetina hodnot funkce READ_HSV
READ_HSV_SAT("cesta")
pro
druhá třetina hodnot funkce READ_HSV
READ_HSV_VALUE("cesta") pro
poslední třetina hodnot funkce READ_HSV
WRITE("cesta")
zapsat hodnoty s maximální přesností (bez
ohledu na formát zobrazení) oddělené mezerami
do datového souboru (ignoruje fyzikální
jednotky)
WRITEPRN("cesta")
zapsat pole hodnot do datového souboru
(obdobně jako u funkce WRITE)
WRITEBMP("cesta")
zapsat pole hodnot do souboru - černobílého
obrázku
WRITERGB("cesta")
zapsat pole hodnot (red, green, blue) do souboru
- barevného obrázku (.bmp)
WRITE_HLS("cesta")
pro
zapsat pole hodnot (hue, lightness, saturation) do
souboru - barevného obrázku (.bmp)
WRITE_HSV("cesta")
pro
zapsat pole hodnot (hue, saturation, value) do
souboru - barevného obrázku (.bmp)
APPEND("cesta")
připojit hodnoty
souboru
do
existujícího
datového
APPENDPRN("cesta")
připojit pole hodnot do existujícího datového
souboru
T ídicí funkce
sort(v)
seřadí prvky vektoru v ve vzestupném pořadí
csort(A, n)
seřadí řádky matice A tak, aby hodnoty v n-tém
sloupci neklesaly
rsort(A, n)
seřadí sloupce matice A tak, aby hodnoty v n-tém
řádku neklesaly
reverse(v)
seřadí prvky vektoru v v obráceném pořadí
reverse(A)
seřadí řádky matice A v obráceném pořadí
Seznamy
125
Zaokrouhlovací funkce
floor(x)
největší celé číslo menší nebo rovno x
ceil(x)
nejmenší celé číslo větší nebo rovno x
Statistické funkce
mean(A)
aritmetický průměr prvků pole A
median(A)
medián prvků pole A
var(A)
variance prvků pole A o velikosti m x n podle
vztahu:
1 .
m.n
m
1 n
1
Ai , j
i =0
mean ( A )
2
j =0
stdev(A)
směrodatná odchylka prvků pole A (odmocnina
z hodnoty var(A))
Var(A)
variance prvků pole A o velikosti m x n podle
vztahu:
m
1
m.n
1 n
1
.
1
Ai , j
i =0
mean ( A )
2
j =0
Stdev(A)
směrodatná odchylka prvků pole A (odmocnina
z hodnoty Var(A))
cvar(A, B)
kovariance prvků polí A, B
corr(A, B)
Pearsonův korelační koeficient polí A, B
Distribu ní funkce
hist(int, A)
vektor zobrazující počet dat pole A, která padla
do intervalů daných vektorem mezí int
(histogram)
rbeta(m, s1, s2)
vektor m náhodných čísel,1 která mají beta
rozdělení s tvarovými parametry s1 a s2
dbeta(x, s1, s2)
pravděpodobnost x při beta rozdělení
1
Sekvence všech náhodných čísel v Mathcadu se generují na základě hodnoty (seed
value for random numbers), kterou můžeme změnit pomocí položky menu Math,
Options na straně Built-In Variables.
Seznamy
126
pbeta(x, s1, s2)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při beta rozdělení
qbeta(p, s1, s2)
inverze funkce pbeta při beta rozdělení
rbinom(m, n, p)
vektor m náhodných čísel, která mají binomické
rozdělení
dbinom(k, n, p)
pravděpodobnost, že náhodná proměnná bude
mít hodnotu k při binomickém rozdělení
pbinom(k, n, p)
kumulativní hodnota pravděpodobnosti k
výskytů jevu v n pokusech při binomickém
rozdělení
qbinom(p, n, q)
počet výskytů jevu při n pokusech, jestliže jejich
pravděpodobnost je p, q je pravděpodobnost
tohoto jevu v jednom pokusu
rnbinom(m, n, p)
vektor m náhodných čísel, která mají negativní
binomické rozdělení
dnbinom(k, n, p)
pravděpodobnost, že náhodná proměnná bude
mít hodnotu k při negativním binomickém
rozdělení
pnbinom(k, n, p)
kumulativní hodnota pravděpodobnosti
negativním binomickém rozdělení
qnbinom(p, n, q)
inverze negativního binomického rozdělení
o velikosti n a pravděpodobnosti nezdaru q
rcauchy(m, l, s)
vektor m náhodných čísel, která mají Cauchyho
rozdělení
dcauchy(x, l, s)
pravděpodobnost x při Cauchyho rozdělení
pcauchy(x, l, s)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při Cauchyho rozdělení
qcauchy(p, l, s)
inverze funkce pcauchy při Cauchyho rozdělení
rchisq(m, d)
vektor m náhodných čísel, která mají rozdělení
chi-kvadrát a stupeň volnosti d
dchisq(x, d)
pravděpodobnost x při rozdělení chi-kvadrát
pchisq(x, d)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při rozdělení chi-kvadrát
qchisq(p, d)
inverze funkce pchisq při rozdělení chi-kvadrát
Seznamy
při
127
rexp(m, r)
vektor m náhodných
exponenciální rozdělení
dexp(x, r)
pravděpodobnost x při exponenciálním rozdělení
pexp(x, r)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při exponenciálním
rozdělení
qexp(p, r)
inverze funkce
rozdělení
rF(m, d1, d2)
vektor m náhodných čísel, která mají F rozdělení
a stupně volnosti d1 a d2
dF(x, d1, d2)
pravděpodobnost x při F rozdělení
pF(x, d1, d2)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při F rozdělení
qF(p, d1, d2)
inverze funkce pF při F rozdělení
rgamma(m, s)
vektor m náhodných čísel, která mají gamma
rozdělení s tvarovým parametrem s
dgamma(x, s)
pravděpodobnost x při gamma rozdělení
pgamma(x, s)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při gamma rozdělení
qgamma(p, s)
inverze funkce pgamma při gamma rozdělení
rgeom(m, p)
vektor m náhodných
geometrické rozdělení
dgeom(k, p)
pravděpodobnost, že náhodná proměnná bude
mít hodnotu k při geometrickém rozdělení
pgeom(k, p)
kumulativní hodnota pravděpodobnosti
geometrickém rozdělení
qgeom(p, q)
inverze geometrického rozdělení, q je
pravděpodobnost výskytu jevu v jednom pokusu
rlnorm(m, µ, σ)
vektor m náhodných čísel, která mají
logaritmické normální rozdělení, µ je logaritmus
průměrné hodnoty a σ logaritmus směrodatné
odchylky
dlnorm(x, µ, σ)
pravděpodobnost x při logaritmickém normálním
rozdělení
plnorm(x, µ, σ)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při logaritmickém
Seznamy
pexp
čísel,
při
která
mají
exponenciálním
čísel,
která
mají
při
128
normálním rozdělení
Seznamy
129
qlnorm(p, µ, σ)
inverze funkce plnorm
normálním rozdělení
rlogis(m, l, s)
vektor m náhodných čísel, která mají logistické
rozdělení
dlogis(x, l, s)
pravděpodobnost x při logistickém rozdělení
plogis(x, l, s)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při logistickém rozdělení
qlogis(p, l, s)
inverze funkce plogis při logistickém rozdělení
rnorm(m, µ, σ)
vektor m náhodných čísel, která mají normální
rozdělení, µ je průměrná hodnota a σ
směrodatná odchylka
dnorm(x, µ, σ)
pravděpodobnost x při normálním rozdělení
cnorm(x)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při normovaném
normálním rozdělení
pnorm(x, µ, σ)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při normálním rozdělení
qnorm(p, µ, σ)
inverze funkce pnorm při normálním rozdělení
rpois(m, λ)
vektor m náhodných čísel, která mají Poissonovo
rozdělení
dpois(k, λ)
pravděpodobnost, že náhodná proměnná bude
mít hodnotu k při Poissonově rozdělení
ppois(k, λ)
kumulativní hodnota
Poissonově rozdělení
qpois(p, λ)
inverze Poissonova rozdělení
rt(m, d)
vektor m náhodných čísel, která mají Studentovo
rozdělení a stupeň volnosti d
dt(x, d)
pravděpodobnost x při Studentově rozdělení
pt(x, d)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při Studentově rozdělení
qt(p, d)
inverze funkce pt při Studentově rozdělení
rnd(x)
náhodné číslo rovnoměrného rozdělení mezi 0 a
x
runif(m, a, b)
vektor m náhodných čísel, která mají
rovnoměrné rozdělení na intervalu s koncovými
Seznamy
při
logaritmickém
pravděpodobnosti
při
130
body a, b
dunif(x, a, b)
pravděpodobnost x při rovnoměrném rozdělení
punif(x, a, b)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při rovnoměrném
rozdělení
qunif(p, a, b)
inverze funkce punif při rovnoměrném rozdělení
rweibull(m, s)
vektor m náhodných čísel, která mají Weibullovo
rozdělení s tvarovým parametrem s
dweibull(x, s)
pravděpodobnost x při Weibullově rozdělení
pweibull(x, s)
pravděpodobnost hodnoty menší nebo rovné x
(bod součtové křivky) při Weibullově rozdělení
qweibull(p, s)
inverze funkce
rozdělení
pweibull
při
Weibullově
Interpola ní a extrapola ní funkce
linterp(vx, vy, x)
hodnoty dané lineární interpolací v bodech x
lspline(vx, vy)
vektor druhých derivací pro vytvoření spline
křivky využívaný funkcí interp, lineární okrajové
podmínky
lspline(Mxy, Mz)
vektor druhých derivací pro vytvoření spline
plochy využívaný funkcí interp, lineární
okrajové podmínky
pspline(vx, vy)
vektor druhých derivací pro vytvoření spline
křivky využívaný funkcí interp, parabolické
okrajové podmínky
pspline(Mxy, Mz)
vektor druhých derivací pro vytvoření spline
plochy využívaný funkcí interp, parabolické
okrajové podmínky
cspline(vx, vy)
vektor druhých derivací pro vytvoření spline
křivky využívaný funkcí interp, kubické
okrajové podmínky
cspline(Mxy, Mz)
vektor druhých derivací pro vytvoření spline
plochy využívaný funkcí interp, kubické
okrajové podmínky
interp(vs, vx, vy, x)
hodnoty dané kubickou interpolací v bodech x,
vs je vektor získaný pomocí funkcí lspline,
pspline nebo cspline
interp(vs, Mxy, Mz, v)
hodnoty dané kubickou interpolací v bodech x, y
určených vektorem v, vs je vektor získaný
pomocí funkcí lspline, pspline nebo cspline
Seznamy
131
vektor n předpověděných hodnot založených na
m za sebou jdoucích prvcích vektoru v
(extrapolace)
predict(v, m, n)
Regresní funkce
slope(vx, vy)
sklon regresní přímky
intercept(vx, vy)
posunutí regresní přímky (y = slope x +
intercept)
regress(vx, vy, n)
vektor vyžadovaný funkcí interp k nalezení
regresního polynomu n-tého stupně, který
nejlépe vyhovuje hodnotám vx, vy
regress(Mxy, vz, n)
vektor vyžadovaný funkcí interp k nalezení
regresního polynomu n-tého stupně, který
nejlépe
vyhovuje
hodnotám
Mxy,
vz
(vícenásobná regrese)
loess(vx, vy, span)
pro
vektor vyžadovaný funkcí interp k nalezení
regresního polynomu druhého stupně, který
nejlépe vyhovuje hodnotám vx, vy v okolí daném
hodnotou span (lokální regrese)
loess(Mxy, vz, span)
pro
vektor vyžadovaný funkcí interp k nalezení
regresního polynomu druhého stupně, který
nejlépe vyhovuje hodnotám Mxy, vy v okolí
daném hodnotou span (lokální vícenásobná
regrese)
interp(vs, vx, vy, x)
interpolované hodnoty v bodech x, vs je vektor
získaný pomocí funkce regress nebo loess
interp(vs, Mxy, vz, v)
interpolované hodnoty v bodech x, y daných
vektorem v, vs je vektor získaný pomocí funkce
regress nebo loess
linfit(vx, vy, F)
vektor obsahující koeficienty, které použijeme
k lineární kombinaci funkcí daných vektorem F
genfit(vx, vy, vg, F)
vektor obsahující parametry a, b, ... regresní
funkce typu f(x) = f1(a x) + f2(b x) + ...
Seznamy
132
Funkce pro vyhlazení graf
vektor vyhlazených hodnot vy vytvořený pomocí
mediánů, n je velikost vyhlazovaného okna
medsmooth(vy, n)
ksmooth(vx, vy, b)
pro
vektor vytvořený užitím Gaussova jádra
k výpočtu vážených průměrů hodnot vy, b je
velikost vyhlazovaného okna
supsmooth(vx, vy)
pro
vektor vyhlazených hodnot vy pomocí metody
nejmenších čtverců použité ve vyhlazovaném
okně, jehož rozměr je vybírán automaticky pro
různé části dat
Komplexní funkce
Re(z)
reálná část komplexního čísla z
Im(z)
imaginární část komplexního čísla z
arg(z)
úhel příslušný číslu z v komplexní rovině
Podmínkové a další nespojité funkce
if(cond, z1, z2)
hodnota z1, pokud je podmínka cond splněna,
hodnota z2, když není splněna
until(x, z)
hodnota z, dokud výraz x, který může obsahovat
proměnnou hodnotu, není záporný (použije se
např. pro zastavení iterací, když chyba dosáhne
malé hodnoty)
δ(m, n)
hodnota 1, pokud m = n, hodnota 0 v ostatních
případech
ε(i, j, k)
hodnota 1, pokud jsou argumenty sudou
permutací čísel 0, 1, 2, hodnota -1, pokud jsou
lichou permutací čísel 0, 1, 2 a hodnota 0, pokud
jsou alespoň dva argumenty stejné
Φ(x)
hodnota 0, pokud je x záporné, hodnota 1
v ostatních případech
Seznamy
133
Funkce pro ešení diferenciálních rovnic
Podrobný přehled těchto funkcí a jejich argumentů včetně p íklad je v nápovědě.
Numerické řešení obyčejných diferenciálních rovnic a soustav dostáváme ve formě
matice, kde v prvním sloupci jsou nezávisle proměnné a v dalších hodnoty hledaných
funkcí a jejich derivací v těchto bodech.
ř
ů
řešení obyčejných diferenciálních rovnic n-tého
řádu a soustav těchto rovnic metodou RungeKutta
rkfixed(vy, x1, x2, i, D)
Rkadapt(vy, x1, x2, i, D)
pro
řešení obyčejných diferenciálních rovnic n-tého
řádu metodou Runge-Kutta s proměnnou
hodnotou kroku (pro pomalu se měnící funkce)
Bulstoer(vy, x1, x2, i, D)
pro
řešení obyčejných diferenciálních rovnic n-tého
řádu metodou Bulirsch-Stoer (pro hladké funkce)
Stiffb(vy, x1, x2, i, D, J)
pro
řešení soustav obyčejných diferenciálních rovnic
n-tého řádu metodou Bulirsch-Stoer v případech,
že řešení pomocí funkce rkfixed je nestabilní
(matice soustavy se blíží singulární)
Stiffr(vy, x1, x2, i, D, J)
pro
řešení soustav obyčejných diferenciálních rovnic
n-tého řádu metodou Rosenbrock v případech, že
řešení pomocí funkce rkfixed je nestabilní
(matice soustavy se blíží singulární)
rkadapt(vy, x1, x2, p, D, k, d) pro
odpovídá funkci Rkadapt, avšak dostáváme
řešení pouze v některých bodech (x2), ve kterých
nás zajímá
bulstoer(vy, x1, x2, p, D, k, d) pro
odpovídá funkci Bulstoer, avšak dostáváme
řešení pouze v některých bodech (x2), ve kterých
nás zajímá
stiffb(vy, x1, x2, p, D, J, k, d)
pro
odpovídá funkci Stiffb, avšak dostáváme řešení
pouze v některých bodech (x2), ve kterých nás
zajímá
stiffr(vy, x1, x2, p, D, J, k, d)
pro
odpovídá funkci Stiffr, avšak dostáváme řešení
pouze v některých bodech (x2), ve kterých nás
zajímá
sbval(vg, x1, x2, D, vy, vd)
pro
chybějící počáteční podmínky pro řešení dif.
rovnic
bvalfit(vg1,vg2,x1,x2,xf,D,vy1,vy2,vd)
pro
chybějící okrajové podmínky pro řešení dif.
rovnic, pokud známe hodnoty v x1 a x2
Seznamy
134
relax(a, b, c, d, e, f, u, rj)
pro
řešení Poissonovy parciální diferenciální rovnice
ve čtvercovém intervalu
multigrid(M, ncycle)
pro
řešení Poissonovy parciální diferenciální rovnice
ve čtvercovém intervalu, jestliže na všech
čtyřech stranách hranice je hodnota hledané
funkce 0
Transforma ní funkce
fft(v)
Fourierova transformace reálných hodnot ve
vektoru v
FFT(v)
Fourierova transformace reálných hodnot
s mírně odlišnou transformační funkcí (dle R.
Bracewella)
ifft(u)
inverze funkce fft, hodnota v, pokud u = fft(v)
IFFT(u)
inverze funkce FFT, hodnota v, pokud u
=FFT(v)
cfft(A)
Fourierova
transformace
komplexních hodnot v poli A
CFFT(A)
Fourierova
transformace
reálných
nebo
komplexních hodnot v poli A s mírně odlišnou
transformační funkcí (dle R. Bracewella)
icfft(B)
inverze funkce cfft, hodnota A, pokud B = cfft(A)
ICFFT(B)
inverze funkce CFFT, hodnota A, pokud
B = CFFT(A)
reálných
nebo
wave(v)
pro
diskrétní wavelet (vlnová) transformace reálných
hodnot
iwave(u)
pro
inverze funkce
u = wave(v).
wave,
Besselovy funkce
I0(x)
Besselova funkce I0(x)
I1(x)
Besselova funkce I1(x)
In(m, x)
Besselova funkce Im(x)
J0(x)
Besselova funkce J0(x)
J1(x)
Besselova funkce J1(x)
Jn(m, x)
Besselova funkce Jm(x)
K0(x)
Besselova funkce K0(x)
K1(x)
Besselova funkce K1(x)
Seznamy
hodnota
v,
jestliže
135
Kn(m, x)
Besselova funkce Km(x)
Y0(x)
Besselova funkce Y0(x)
Y1(x)
Besselova funkce Y1(x)
Yn(m, x)
Besselova funkce Ym(x)
et zcové funkce
concat(S1, S2)
pro
nový řetězec, který vznikne připojením řetězce
S2 za S1
strlen(S)
pro
počet znaků v řetězci S
search(S1, SubS, m)
pro
pořadí prvního znaku části SubS v řetězci S1
(hledání se provádí od pozice m) nebo -1, pokud
SubS není nalezen
substr(S, m, n)
pro
část řetězce S, začínající na m-té pozici s počtem
znaků n (pozice prvního znaku řetězce je 0)
str2num(S)
pro
převede číselný řetězec S na číslo
num2str(z)
pro
převede číslo z na číselný řetězec
str2vec(S)
pro
převede řetězec znaků S do vektoru ASCII kódů
vec2str(v)
pro
převede vektor v kódů ASCII (0 až 255) na
řetězec znaků
error(S)
pro
řetězec S zobrazený jako chybové hlášení
Další funkce
mod(x, y)
zbytek při dělení x / y
angle(x, y)
úhel mezi osou x a spojnicí počátku s bodem
(x, y)
Γ(z)
Eulerova gamma funkce:
∞
t
z
1.
t
e dt
0
erf(x)
chybová funkce:
x
2 . t2
e dt
π
0
Další vestavěné funkce najdete v některých elektronických příručkách (Function
Pack) - viz. kap. 15.2, nebo si je ve verzi Mathcad Professional můžete vytvořit sami
(uživatelská DLL).
Seznamy
136
Vývoj verzí Mathcadu
Pokro ilá matematika:
Maticové operace
Řešení diferenciálních
rovnic
Živé symbolické výpočty
Symbolická řešení
soustav rovnic
Paleta symbolických
operátorů
Řada statistických funkcí
Regresní analýza a
vyhlazení dat
Programování:
Operátory pro vytváření
programů
Programování se živými
symbolickými výrazy
Použití řetězcových
proměnných
Průběžné ošetření chyb
(On Error)
Práce s daty:
Přesun dat do (z)
Mathcadu
Datové filtry pro Excel,
MATLAB, 1-2-3, ASCII
Nástroje pro řízení toku
dat (MathConnex)
Možnost rozší ení:
Vytváření vlastních
funkcí v C/C++
Další funkce ve
speciálních příručkách
Vlastní knihovny funkcí
Vytváření uživatelské
symboliky
Práce s jednotkami:
Převádění jednotek
Soustava jednotek MKS,
CGS, U.S.
Jednotky SI
č
ř
5
PLUS 5
6.0 SE
PLUS 6
⇑
7 PRO
⇑
⇑
⇑
⇑
⇑
⇑
5
PLUS 5
6.0 SE
PLUS 6
7 PRO
⇑
5
PLUS 5
6.0 SE
PLUS 6
7 PRO
⇑
5
PLUS 5
6.0 SE
PLUS 6
7 PRO
5
PLUS 5
6.0 SE
PLUS 6
7 PRO
Seznamy
137
Vizualizace:
2-D a 3-D grafy
Rychlé grafické
zobrazení funkcí
(QuickPlot)
Propojení s programem
Axum pro tvorbu grafů
Zpracování obrazu
Animace
Práce s dokumentem:
Nastavení vzhledu
stránky a prohlídka před
tiskem
Oddělitelné palety
nástrojů
Export ve formátu RTF
Uzamykání oblastí
Zjednodušené úpravy
vztahů (jako u textů)
Šablony, styly
Využití sítí:
Hyperlink na intranet
nebo WWW
Přístup na Internet přímo
z Mathcadu
Konference uživatelů
Mathcadu na Internetu
(Collaboratory)
Podpora E-mailu na bázi
MAPI
Ovládání programu:
Interaktivní výuka
Příklady výpočtů
(QuickSheets)
Obnovované příklady na
síti
Návody k řešení
problémů
Kontextová nápověda
5
PLUS 5
6.0 SE
PLUS 6
7 PRO
⇑
⇑
⇑
5
PLUS 5
6.0 SE
PLUS 6
7 PRO
⇑
5
PLUS 5
6.0 SE
PLUS 6
7 PRO
5
PLUS 5
6.0 SE
PLUS 6
7 PRO
⇑
⇑
⇑
⇑
Další informace o novinkách ve verzi Mathcad 7 jsou v kapitole 2.
Seznamy
Podobné dokumenty
Příručka Mathcad
 8.2.4 Matematické operace s vektory...................................................................33
8.2.5 Operace s jednotlivými prvky.............................................................
8.2.4 Matematické operace s vektory...................................................................33
8.2.5 Operace s jednotlivými prvky.............................................................
Pro pokročilé - Industry Online Support
 Koeficienty a2, a3, a4 a a5 jsou popsány svou
hodnotou, rozsahem hodnot a jednotkou. Poslední
koeficient může odpadnout, jestliže má nulovou
hodnotu.
Koeficienty a2, a3, a4 a a5 jsou popsány svou
hodnotou, rozsahem hodnot a jednotkou. Poslední
koeficient může odpadnout, jestliže má nulovou
hodnotu.
Základní příkazy v R
 funkce z balíčku TSA sloužící
pro specifikaci ARMA modelu
rozšířená autokorelační funkce
funkce z balíčku TSA sloužící
pro specifikaci ARMA modelu
rozšířená autokorelační funkce
RB-digital.sk | Chiptuning Lancia Lybra 2.4 JTD
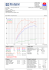 meranie výkonu:
Branislav Hanko
Družstevná 6
038 53 Turany
Tel.:0908 967555
Typ vozidla:
Reg. značka:
Technik:
meranie výkonu:
Branislav Hanko
Družstevná 6
038 53 Turany
Tel.:0908 967555
Typ vozidla:
Reg. značka:
Technik:
jaro - HSIcom
 a jeho umístění na základě čísla projektu,
oblasti do které spadá, případně na základě názvu projektu (nebo jeho části), poznámky (nebo její části) a pomocí dalších
identifikátorů, které archivář p...
a jeho umístění na základě čísla projektu,
oblasti do které spadá, případně na základě názvu projektu (nebo jeho části), poznámky (nebo její části) a pomocí dalších
identifikátorů, které archivář p...
29.05.2013 1 Engineering report
 Externí obrázek
Rastrové obrázky (jpg, png, bmp, …)
Vektorové
V kt
é obrázky
b á k ((wmf,
f emf)
f)
Scia Engineer obrázky (ep3)
3D obrázky (DWG, VRML)
Pokud jeden rozměr = 0 dopočítán a...
Externí obrázek
Rastrové obrázky (jpg, png, bmp, …)
Vektorové
V kt
é obrázky
b á k ((wmf,
f emf)
f)
Scia Engineer obrázky (ep3)
3D obrázky (DWG, VRML)
Pokud jeden rozměr = 0 dopočítán a...
Normální rozdělení a centrální limitní věta
 B Příklad 9.1. Najděte generující funkci pro náhodnou veličinu X s binomickým rozdělením s para2 = np(1 − p).
metry n, p a ověřte, že E(X) = np, σX
Víme, že pro náhodnou veličinu X definovanou v pr...
B Příklad 9.1. Najděte generující funkci pro náhodnou veličinu X s binomickým rozdělením s para2 = np(1 − p).
metry n, p a ověřte, že E(X) = np, σX
Víme, že pro náhodnou veličinu X definovanou v pr...
MSR 500 - MM racing
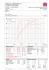 MM RACING s.r.o. - chiptuning a meranie výkonu
Pri Starom Letisku 1, 831 07 BRATISLAVA
www.mmracing.sk, [email protected]
MM RACING s.r.o. - chiptuning a meranie výkonu
Pri Starom Letisku 1, 831 07 BRATISLAVA
www.mmracing.sk, [email protected]
 Prokluz
Rychlost bez zátěže
Otáčky bez zátěže
Rychlost s plnou zátěží
Prokluz
Rychlost bez zátěže
Otáčky bez zátěže
Rychlost s plnou zátěží
