cp= ∂H cV= ∂U
Transkript
1. věta termodynamická, vnitřní energie U=QW uzace: energie dodaná do systému (ve formě tepla či práce) je kladná, energie odevzdaná systémem do okolí je záporná objemová práce V2 W=− ∫ pvnější dV vratný děj: nevratný děj: vnější V1 vnitřní p =p = pT ,V - dosadí se ze stavové rovnice vnější p ḱonst. dU =dQ – pdV ⇒ U=Q [V] enthalpie: H=U pV ⇒ H=U pV H=Q [ p] tepelné kapacity ∂ Hm ∂H ;c p,m= ∂T p ∂T p ∂U m ∂U cV= ;cV ,m= ∂T V ∂T V * * H ,U - závisá pouze na teplotě, tedy: U= H=0 [T , id.plyn] Id. plyn (Meyerův vztah): c*p,m – c*V , m=R cp= adiabatický děj: Q = 0 vratný konaný id. Plynem cv = konst. Adiabatický exponent: = m cp,m cV ,m Poissonova rovnice: pV m=konst. ⇒ p1Vm,1= p2V m,2 13-2 Vnitřní energii argonu ve stavu ideálního plynu při 25°C a tlaku 101,325 kPa byla přisouzena hodnota 3718 Jmol–1. Jaká je odpovídající hodnota molární entalpie argonu? Předpokládejte platnost stavové rovnice ideálního plynu. Hm=U m pV m ideální plyn = UmRT=37188,314⋅ 273,1525=6196,96 Jmol−1 13-3 Do autoklávu o objemu 1 dm3, naplněného neideálním plynem, bylo dodáno teplo Q = 5000 J. Přitom se zvýšila teplota z 300 K na 400 K a tlak z 200 kPa na 250 kPa. Určete W, ∆U, ∆H. U=QW W=0 [V] ⇒ U=Q=5000 J H= U pV =50001 250−200=5050 J 13-7 Určete práci vyměněnou s okolím při ději, kdy 1 mol argonu z počátečního stavu T1 = 500 K, p1 = 100 kPa přejde do takového stavu, ve kterém bude mít dvakrát větší hustotu než na počátku. Výpočet proveďte pro (a) izotermní, (b) izobarický děj. Předpokládejte, že argon se chová podle stavové rovnice ideálního plynu. V V m,1=41,572 dm3 mol−1 ⇒ V m, 2= m, 1=20,78 dm 3 mol−1 2 a) V V V RT vnější W=−∫ p dV =−∫ dV =−RT ln 2=8,314⋅500 ln 0,5=2881,6 J V V1 V V b) 2 2 1 1 V2 vnější W=−∫ p vnější dV =− p V1 V2 ∫ dV =− pvnější V 2 – V1=2078,6 J V1 14-12 V uzavřené nádobě o objemu 50 dm3 jsou obsaženy dva moly ideálního jednoatomového plynu (cVm = (3/2)R ) o teplotě 25°C. Nádoba je ohřáta na teplotu 125°C. Určete hodnoty Q, W, ∆U, ∆H a počáteční a konečný tlak v systému. nRT1 =99,158 kPa V nRT2 p2= =132,416 kPa V p1= T2 2⋅3 R100=2494,34 J 2 T Q= U=2494,34 J id.plyn H= U pV = U nRT=2494,342⋅R⋅100=4157,24 J W=0⇒ U=n∫ cV ,mdT = 1 13-14 Systému, který obsahoval 1 kg Fe3O4 (M = 231,55 gmol-1), bylo dodáno teplo 400 kJ. Počáteční teplota Fe3O4 je 300 K a jeho tepelná kapacita je dána vztahem c°pm =86,260,20892 T [ JK −1 mol−1 ] Vypočtěte maximální dosažitelnou teplotu při ohřevu probíhajícím za konstantního tlaku. n= T2 1000 =4,3187 mol 231,55 Q= H [ p] [ H=n∫ cp,mdT =n 86,26T2 – T1 T1 0,20892 2 2 T2 – T1 2 ] 92620=0,10446 T2286,26 T2 – 35279,4 T2=768,16 K 3-16 Vypočítejte (a) na jakou teplotu se ohřeje vzduch ve válci s pohyblivým pístem při vratné adiabatické kompresi, (b) jaký je ve válci tlak po kompresi, (b) objemovou práci. Počáteční teplota vzduchu je 350 K, počáteční tlak je 100 kPa a objem před kompresí je 506,3 cm3. Poměr maximálního a minimálního objemu má hodnotu 18. Při výpočtu uvažujte ideální stavové chování. Poissonova konstanta pro vzduch je 1,4. n= p1V 1 100⋅0,5063 = =0,0174 mol RT1 8,314⋅350 Dopočet konečného stavu: cp,m cp,m 29 = = =1,4 cV ,m cp,m−R 29 – 8,314 V1 p2= p1 =100⋅181,4=5,72 Mpa V2 pV T2= 2 2 =1112,23 K nR výpočet adiabatické práce – MUSÍ SE POUŽÍT VZTAH U=W = T2 W= U=n∫ cV ,mdT =ncV ,mT 2 – T1=0,0174⋅29 – 8,3141112,23 – 350=275,68 J T1 14-18 Určete konečný stav systému a práci vykonanou při nevratné adiabatické expanzi 1 mol ideálního plynu. Počáteční stav systému: p1 = 0,2 MPa, Vm1 = 5 dm3mol-1, cVm = 20,8 JK-1mol-1. Expanze probíhá proti stálému vnějšímu tlaku p2: a) po = 0,16 MPa, (b) po = 0,10 MPa, c) po = 0,04 MPa, d) po = 0,01 MPa.) nevratný adiabatický děj – nelze použít Poissonovy rovnice pro dopočet konečného stavu systému!!!!! zde plyn expanduje proti vnějšímu tlaku: vnější tlak pvnější je tedy roven konečnému tlaku p2 U=W T2 V2 ∫ cV , mdT =−∫ pvnější dV T1 V1 cV , mT2 – T1=− p2Vm,2 – Vm,1 RT 2 RT1 cV ,mT2 – T1=− p2 – p2 p1 ........ p cV , mT1 2 RT1 p1 T2= cV ,mR T2=103,097 K Práce: Vm,2 vnější W=− ∫ p Vm,1 vnější dV =− p V m,2 – V m,1=−0,18572 – 5000=−357,2 J
Podobné dokumenty
Dodatkové veličiny
 ρ = 1,1783 gcm–3. Hustoty čistých složek při 20°C mají tyto hodnoty:
ρ •(H2O) = 0,9982 gcm–3, ρ •(H2SO4) = 1,8305 gcm-3. Vypočtěte:
(a) hustotu tohoto roztoku podle Amagatova zákona,
(b) dodatkový ...
ρ = 1,1783 gcm–3. Hustoty čistých složek při 20°C mají tyto hodnoty:
ρ •(H2O) = 0,9982 gcm–3, ρ •(H2SO4) = 1,8305 gcm-3. Vypočtěte:
(a) hustotu tohoto roztoku podle Amagatova zákona,
(b) dodatkový ...
Katalogový list
 to
bez
ohledu
na
to,
zda
se
jedná
o
malé
nebo
velké
odpadní
nádoby.
Vysokotlaký
systém
mytí
odpadních
nádob
zahrnuje
dvě
s...
to
bez
ohledu
na
to,
zda
se
jedná
o
malé
nebo
velké
odpadní
nádoby.
Vysokotlaký
systém
mytí
odpadních
nádob
zahrnuje
dvě
s...
2. věta termodynamiky
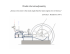 Uvažujme soustavu dvou simultánně pracujících tepelných strojů s týmiž tepelnými
rezervoáry, ale s různými účinnostmi, η1 > η2. Stroj s účinností η2 pracuje v opačném směru,
t.j. čerpá teplo z chla...
Uvažujme soustavu dvou simultánně pracujících tepelných strojů s týmiž tepelnými
rezervoáry, ale s různými účinnostmi, η1 > η2. Stroj s účinností η2 pracuje v opačném směru,
t.j. čerpá teplo z chla...
Termodynamika a molekulová fyzika
 T [K ] = t [°C] + 273,15 °C = t + T0 , Kelvinova (absolutní) teplotní stupnice
T0 = 273,15 K
T [K ] = t [°C] + 273,15 °C = t + T0 , Kelvinova (absolutní) teplotní stupnice
T0 = 273,15 K
Atmosféra Země - jak ji vidí fyzikální chemie
 V atmosféře je ovšem možné nalézt i celou řadu dalších látek, jejich koncentrace jsou však již
tak nízké, že je výhodnější je vyjadřovat raději než v procentech v jednotkách v atmosferické
chemii o...
V atmosféře je ovšem možné nalézt i celou řadu dalších látek, jejich koncentrace jsou však již
tak nízké, že je výhodnější je vyjadřovat raději než v procentech v jednotkách v atmosferické
chemii o...
Čtvrté cvičení z FCH2 – První a druhá věta
 této reakce při 25 oC je 172,464 kJ/mol. Spočítejte teplo, které je spotřebováno, pokud: a) reaktanty
přivádíme při teplotě 798,15 K, produkty odvádíme při 25 oC; b) reaktanty přivádíme při teplotě...
této reakce při 25 oC je 172,464 kJ/mol. Spočítejte teplo, které je spotřebováno, pokud: a) reaktanty
přivádíme při teplotě 798,15 K, produkty odvádíme při 25 oC; b) reaktanty přivádíme při teplotě...
Státní bakalářská zkouška 10. 7. 2007 Fyzika (učitelství) Zkouška
 • Při řešení smíte používat kalkulačku.
• Fyzikální konstanty a materiálové parametry, které budete při řešení potřebovat, jsou na konci
testu.
• Pracujte samostatně! Při pokusu o spolupráci s osta...
• Při řešení smíte používat kalkulačku.
• Fyzikální konstanty a materiálové parametry, které budete při řešení potřebovat, jsou na konci
testu.
• Pracujte samostatně! Při pokusu o spolupráci s osta...
Dodatkové veličiny
 Do velké nádrže obsahující směs ethanolu (30 mol.%) a vody (70 mol.%) bylo
přidáno 1000 cm3 ethanolu (hustota čistého ethanolu je 0,8 gcm–3,
M = 46 gmol–1). Objem roztoku se zvětšil o 700 cm3. Urče...
Do velké nádrže obsahující směs ethanolu (30 mol.%) a vody (70 mol.%) bylo
přidáno 1000 cm3 ethanolu (hustota čistého ethanolu je 0,8 gcm–3,
M = 46 gmol–1). Objem roztoku se zvětšil o 700 cm3. Urče...
TERMOCHEMIE, TERMOCHEMICKÉ ZÁKONY
 Entropie: míra neuspořádanosti systému. Čím je systém neuspořádanější, tím je entropie
větší. Entropie se značí S.
Změna entropie: ∆ S
Standardní změna entropie: změna entropie za standardních podm...
Entropie: míra neuspořádanosti systému. Čím je systém neuspořádanější, tím je entropie
větší. Entropie se značí S.
Změna entropie: ∆ S
Standardní změna entropie: změna entropie za standardních podm...
 delokalizované vazby, koordinační vazba. Iontová vazba, stabilita iontů. Vodíková vazba.
P3 – 07.10.2014
V. SKUPENSKÉ STAVY. Plyny: empirické zákony, stavová rovnice ideálního a reálného plynu. Kap...
delokalizované vazby, koordinační vazba. Iontová vazba, stabilita iontů. Vodíková vazba.
P3 – 07.10.2014
V. SKUPENSKÉ STAVY. Plyny: empirické zákony, stavová rovnice ideálního a reálného plynu. Kap...



